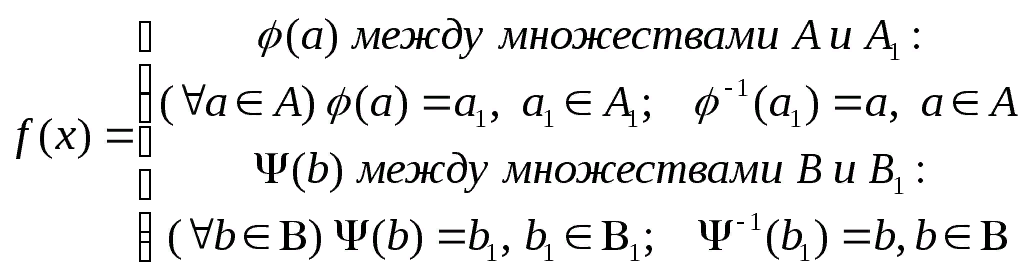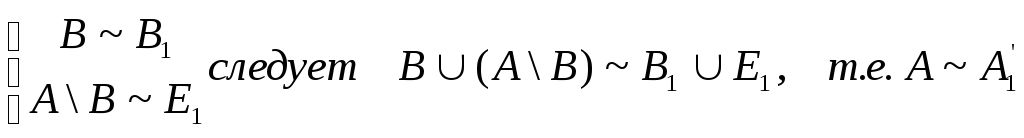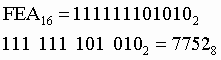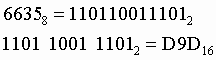Навигация по странице:20. Разность целых неотрицательных чисел . (Задачи, определение, теорема, правила, свойства )Теорема3. Единственность разности.21. Произведение целых неотрицательных чисел (задача, определение, теорема, правила).22. Частное целых неотрицательных чисел (задача, определение, теорема, правила)23. Деление с остатком.24. Алгоритмы сложения, вычитания, умножения и деления натуральных чисел.25. Понятие системы счисления. Позиционные и непозиционные системы счисления.-позиционныеПример.
|
математика ответы. Математика экзамен (вып.). 1. Числовые выражения
II Единственность: покажем, что сумма a+b единственна и не зависит от выбора представителей в классах эквивалентности.
Пусть числа a и b кроме множеств А и В определяют множества А1 и B1, и пусть с1 = m (A1B1). Покажем, что с = с1 (а это будет тогда, когда АВ
A1B1).
Дано: A
A1, B
B1, A1 B1=A B = Ø.
Доказать: A B
A1 B1.
Для того, чтобы показать, что А В
, нужно показать, что между ними существует хотя бы одно взаимно однозначное соответствие. Построим его.
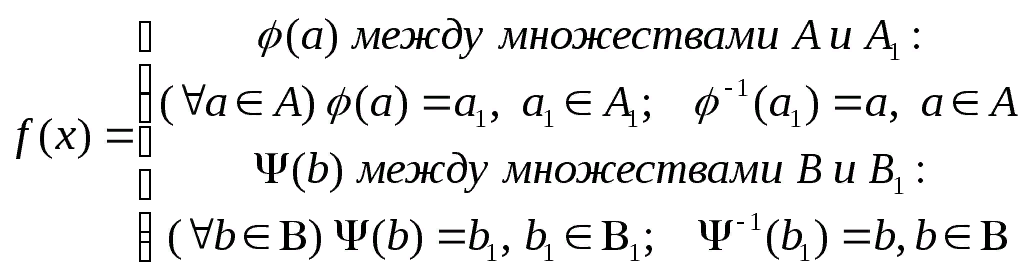 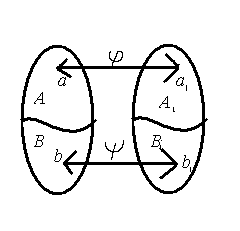
Т.о. будет взаимно однозначно поставлен элемент из множестваА1В1 =>.
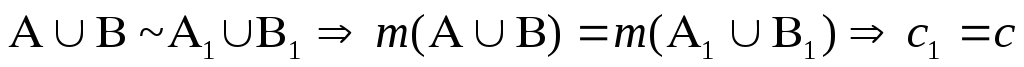
Операция отыскания суммы называется сложением.
20. Разность целых неотрицательных чисел . (Задачи, определение, теорема, правила, свойства )
Определение: Разностью целых неотрицательных чисел а и b называется целое неотрицательное число (a-b), равное числу элементов в дополнении множества В до множества А при условии, что m(A)=a, m(B)=b и BA
а – b = m (A\B), где a = m (A), b = m (B) и BA
Действие отыскания разности называется вычитанием. При этом записывают a – b = c.
Например, A ={a,b,c,d,e,f }, m (A) = 6
B ={b, d, e, f }, m (B) = 4
A\B ={a, c }, m (A\B) = 2 = m (B'A)
m (A\B) =m (A) – m (B)
Из примера видно, что 6 - 4 = 2, где 2 = m (B'A).
Теорема: Разность целых неотрицательных чисел a и b существует и единственна тогда и только тогда, когда b ≤ a.
Доказательство:
1. Необходимость существования разности: Если разность c = a - b существует, то b ≤ a.
Доказательство:
Возможны два случая: с = 0 и с ≠ 0, то есть с > 0.
а) пусть с = 0, тогда так как с = m (A\B), то m (A\B) = c => A\B = Ø. А так как В А, то это означает, что А = В. Тогда m (A) = m (B), то есть a = b.
б) пусть с > 0,то есть m (A\B) > 0 => A\B ≠ Ø и значит B A. Так как А и В конечные множества, то m (B) < m (A), то есть b < a. Объединяя a) и б) получим b ≤ a .
2. Достаточность существования: Если b ≤ a, то разность c = a - b существует.
Доказательство:
Если b ≤ a, то это значит, что (b = a) (b < a).
а) пусть b = a это значит m (B) = m(A). Так как множества А и В – конечные и В А, то это значит, что В = А. тогда A\B = Ø и m (A\B) = 0 => по определению разности имеем a – b = m (A\B) = 0, то есть разность с = 0.
б) пусть b < a, тогда m (B) < m (A). В этом случае имеем, что B A и значит A\B ≠ Ø и m (A\B) ≠ 0, m (A\B) > 0, то есть a – b = m (A\B) =c > 0. И в этом случае существование разности доказано.
3. Единственность разности.
Пусть A
A1 и B
B1, тогда m (A) = m (A1) = a
m (B) = m (B1) = b
Пусть B A, B1 A1 ,тогда a – b = m (A\B) и a – b = m (A1\B1).
Покажем, что m (A\B) = m (A1\B1).
Для этого достаточно показать, что A\B
A1\B1.
Доказательство:
Пусть A\BA1\B1, тогда в одном из множеств, например в A1\B1, можно выделить подмножество Е1, которое будет равномощно A\B.
E1 A1\B1 и A\B
E1
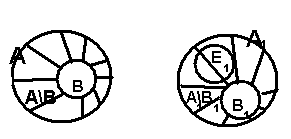
A = (A\B),где B ∩ (A\B) = Ø
Рассмотрим множество А’1=Е1В1, где Е1∩В1=Ø. Очевидно, что A’1 A1.
Из того, что
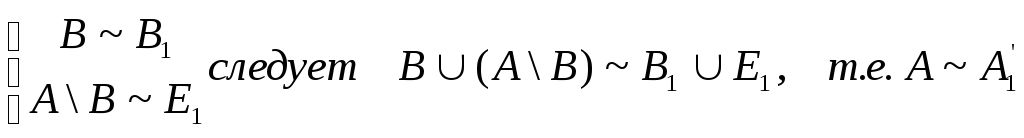
Из того, что A1
A A
A′1 => A1
A′1 (то есть множество равномощно своему собственному подмножеству), а это противоречит определению конечного множества.
Таким образом теорема доказана полностью.
Так как A = B (A\B), то m (A) = m (B(A\B))
Так как B∩(A\B) = Ø, то m (B(A\B)) = m (B) + m (A\B),где m (A) = a, m (B) = b, m (A\B) = a – b.
Тогда будем иметь m (A) = m (B) + m (A\B)
a = b + (a - b).
Отсюда получаем другое определение разности.
Определение: Разностью целых неотрицательных чисел a и b называется целое неотрицательное число (a – b), которое в сумме с числом b дает число а.
Используя теоретико-множественное толкование суммы, разности целых неотрицательных чисел, можно теоретико-множественное толкование всех правил, связывающих операции сложения и вычитания этих чисел.
21. Произведение целых неотрицательных чисел (задача, определение, теорема, правила).
Результатом действия умножения является произведение.
Произведением целых неотрицательных чисел а и в называется такое целое неотрицательное число, которое удовлетворяет следующим условиям:
1. если b > 1 => а * b = а + а +...+ а (b раз)
2. если b = 1 => а * в = а; (а * 1 = а)
3. если b=0 => а * в = 0; (а * 0 = 0)
Пример:
3*4=3+3+3+3=12
3 - слагаемое
4 - количество раз.
1 * 5 = 1 + 1 + 1 + 1 + 1 + 5
5*1=5 (по определению произведения)
0 * 2 = 0 + 0 = 0
2 * 0 = 0 (по определению)
Теоретико-множественный смысл произведения.
Пусть, А - число элементов, в каждом попарно непересекающихся равномощных между собой В множеств.
А = n(А1) = n(А2) =... = n( Аb)
А1, А2,..., Ab - попарно непересекающиеся равномощные между собой множества.
Тогда произведение а * в будем называть числом элементов в объединении этих В множеств.
а * b = n(А1 U А2 U ... U Аb)
Пример:
4 = n(А1) = n(А2) //// - А1
4 * 2 = n(А1 U А2 ) = 8 **** - А2
Определение произведения целых неотрицательных чисел через декартово произведение множеств:
Пусть А – целое неотрицательное число, определяющее число элементов в некотором множестве А, а В – число элементов в некотором множестве В.
а = n(А) и b= n(В).
Тогда, произведением а и в будем называть число элементов в декартовом произведении множеств А и В.
а * b= n(А х В)
Пример:
Пусть 3 – это число элементов во множестве А, а 4 – число элементов во множестве В. Тогда декартово произведение будет содержать 8 элементов. Следовательно: 2 * 4 = 8.
2 * 4
2 = n(А)
4 = n(В)
А х В = 8 => 2 * 4 = 8
Свойства умножения и теоретико-множественная интерпретация.
1) Коммутативное свойство : для любых целых неотрицательных чисел а и b верно равенство: а * b = b * а
2) Ассоциативное : для любых целых неотрицательных чисел а, b и с верно равенство: (а * b) * с = а * (b * с).
3) Дистрибутивное свойство умножения относительно сложения : для любых целых неотрицательных чисел а, b и с верно равенство: (а + b) * с = а * с + b * с.
(а+b)*с = а*с+b*с => А х(ВUC) = (АхВ) и (АхС)
(а-b)*с = а*с-b*с => А х (В\С)=(АхВ) \(АхС)
22. Частное целых неотрицательных чисел (задача, определение, теорема, правила)
Рассмотрим множество А, в котором а элементов. Разобьем его на одинаковые не пересекающиеся подмножества. Они попарно не пересекающиеся и равно
1) если в каждом из этих подмножеств содержится по в элементов, то частным а : в называется число подмножеств в разбиение К
2) если b – число подмножеств в разбиении, то частное чисел а и b – это число элементов в каждом подмножестве разбиения.
6:2=3
Доказательство:
1) А ={1:2:3:4:5:6}
A1 ={1:2}
A2 ={3:4}
A3 ={5:6}
A1 ∩ A2 =A∩A3 =A3∩A1
A1
A2
A3
n (A1) = 2
6:2=3
2) А1 ={1:3:5}
A2 ={2:4:6}
A1 ∩ A2 ,A1∩ A2
6:2=n(A1)=3 ч.т.д.
Определения частного через произведение.
Опр.Частным целого неотрицательного числа а и натурального числа b называется тоже целое неотрицательное число с, что
а: b=с<=>b*c=a (<=> - тогда и только тогда, когда)
Теорема: Для того, чтобы частное а и b существовало, необходимо чтобы b не превосходило а. ( а ≥ b)
Теорема: Если частное существует, то оно единственное. Док-во методом от противного.
Предположим, что частное существует, но оно не существенное.
c1 ≠ c2,,
c1, c2 Є Z (Є Z - принадлежит целым натуральным числам)
a:b=c1
a:b=c2
b*c1=a, b*c2-a => b*c1= b*c2 т.к. b – натуральное, т.е. отличное от 0 число, разделим обе части на 0 => b*c1= b*c2 |: b ≠ 0 => c1= c2 – пришли к противоречию => a* b – единственные.
Обучающимся начальных классов предлагается решить задачу:
«За 3 часа автомобиль проехал 186 км. Какое расстояние проедет автомобиль за 5 ч. если он будет ехать с той же скоростью?»
• О каких величинах идет речь в этой задаче?
• Находятся ли эти величины в функциональной зависимости? Если да, то задайте функцию формулой и поясните, какую величину обозначает каждая буква в записи формулы.
• Измените, данные задачи так, чтобы её можно было решить двумя способами.
23. Деление с остатком.
Деление c остатком — арифметическая операция. Чаще всего эта операция определяется для целых или натуральных чисел.
a=b⋅c+d, где
a– делимое,
b– делитель,
c– неполное частное,
d– остаток.
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если неполное частное умножить на делитель, прибавить остаток. В результате должно получиться делимое. Пример: 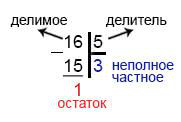
24. Алгоритмы сложения, вычитания, умножения и деления натуральных чисел.
Алгоритм сложения
Сложение однозначных чисел можно выполнить, основываясь на определении этого действия, но чтобы всякий раз не обращаться к определению, все суммы, которые получаются при сложении однозначных чисел, записывают в особую таблицу, называемую таблицей сложения однозначных чисел, и запоминают.
В основе алгоритма сложения многозначных чисел лежат следующие теоретические факты:
- способ записи чисел в десятичной системе счисления;
- свойства коммутативности и ассоциативности сложения;
- дистрибутивность умножения относительно сложения;
- таблица сложения однозначных чисел.
Алгоритм вычитания
Вычитание однозначного числа b из однозначного или двузначного числа а, не превышающего 18, сводится к поиску такого числа с, что b + с = а, и происходит с учетом таблицы сложения однозначных чисел.
Если же числа а и b многозначные и b < а, то смысл действия вычитания остается тем же, что и для вычитания в пределах 20, но техника нахождения разности становится иной: разность многозначных чисел чаще всего находят, производя вычисления столбиком, по определенному алгоритму.
Алгоритм умножения
Умножение однозначных чисел можно выполнить, основываясь на определении этого действия. Но чтобы всякий раз не обращаться к определению, все произведения однозначных чисел записывают в особую таблицу, называемую таблицей умножения однозначных чисел, и запоминают.
Естественно, что смысл умножения сохраняется и для многозначных чисел, но меняется техника вычислений. Произведение многозначных чисел, как правило, находят, выполняя умножение столбиком, по определенному алгоритму.
Алгоритм деления
Когда речь идет о технике деления чисел, то этот процесс рассматривают как действие деления с остатком: разделить целое неотрицательное число а на натуральное число b - это значит найти такие целые неотрицательные числа q и r, что a = bq + r, причем 0≤ r
Выясним сначала, как осуществляется деление на однозначное число. Если на однозначное число делят однозначное или двузначное (не превышающее 89), то используется таблица умножения однозначных чисел. Например, частным чисел 54 и 9 будет число 6, так как 9·6 = 54. Если же надо разделить 51 на 9, то находят ближайшее к нему меньшее число, которое делится на 9 - это число 45, и, следовательно, неполным частным при делении 51 на 9 будет число 5. Чтобы найти остаток, надо из 51 вычесть 45:51 - 45 = 6. Таким образом, 51 = 9·5 + 6, т.е. при делении 51 на 9 получается неполное частное 5 и остаток, равный 6. Записать это можно иначе, при выполнении деления уголком
25. Понятие системы счисления. Позиционные и непозиционные системы счисления.
Система счисления - это совокупность правил и приемов записи чисел с помощью набора цифровых знаков. Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: 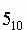 ; ; 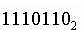 ; ;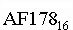 и т. д. и т. д.
Различают два типа систем счисления:
-позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
-непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.
Примером непозиционной системы счисления является римская: числа IX, IV, XV и т.д.
Примером позиционной системы счисления является десятичная система, используемая повседневно.
Любое целое число в позиционной системе можно записать в форме многочлена: 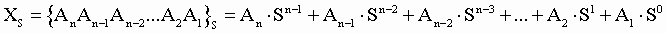
где S- основание системы счисления;
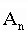 - цифры числа, записанного в данной системе счисления; - цифры числа, записанного в данной системе счисления;
n - количество разрядов числа.
Пример. Число 629310запишется в форме многочлена следующим образом:
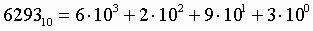
26. Правила перевода чисел из одной системы счисления в другую.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
Пример . Число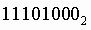 перевести в десятичную систему счисления. перевести в десятичную систему счисления. 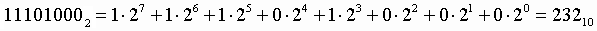
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики: 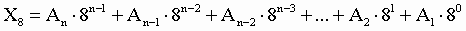
Пример . Число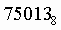 перевести в десятичную систему счисления. перевести в десятичную систему счисления. 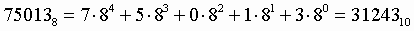
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики: 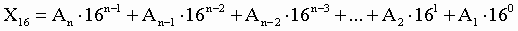
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число 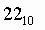 перевести в двоичную систему счисления. перевести в двоичную систему счисления. 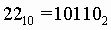 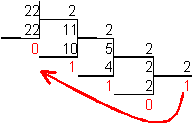
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число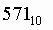 перевести в восьмеричную систему счисления. перевести в восьмеричную систему счисления. 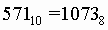 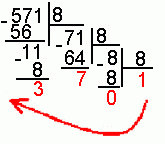
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число 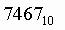 перевести в шестнадцатеричную систему счисления. перевести в шестнадцатеричную систему счисления. 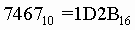 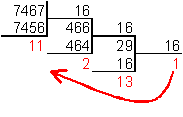
7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой
Пример. Число 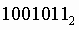 перевести в восьмеричную систему счисления. перевести в восьмеричную систему счисления. 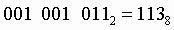
8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой
Пример. Число 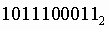 перевести в шестнадцатеричную систему счисления. перевести в шестнадцатеричную систему счисления. 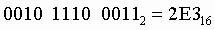
9. Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Пример. Число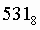 перевести в двоичную систему счисления. перевести в двоичную систему счисления.
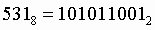
10. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример. Число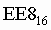 перевести в двоичную систему счисления. перевести в двоичную систему счисления. 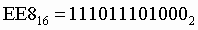
11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример 1. Число 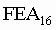 перевести в восьмеричную систему счисления. перевести в восьмеричную систему счисления. 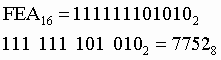
Пример 2. Число 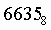 перевести в шестнадцатеричную систему счисления. перевести в шестнадцатеричную систему счисления. 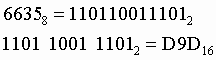 |
|
|
 Скачать 0.71 Mb.
Скачать 0.71 Mb.