математика ответы. Математика экзамен (вып.). 1. Числовые выражения

• Название: 1. Числовые выражения
• Анкор: математика ответы
• Дата: 20.01.2021
• Размер: 0.71 Mb.
• Имя файла: Математика экзамен (вып.).docx
• Тип: Документы; #170002
• страница: 2 из 3

Индукция и дедукция.

Индукцией называют переход от частных утверждений к общим. Напротив, переход от общих утверждений к частным называется дедукцией.

Пример частного утверждения: 254 делится на 2 без остатка.

Из этого частного утверждения можно сформулировать массу более общих утверждений, причем как истинных так и ложных. К примеру, более общее утверждение, что все целые числа, оканчивающиеся четверкой, делятся на 2 без остатка, является истинным, а утверждение, что все трехзначные числа делятся на 2без остатка, является ложным.

Таким образом, индукция позволяет получить множество общих утверждений на основе известных или очевидных фактов. А метод математической индукции призван определить справедливость полученных утверждений.

В качестве примера, рассмотрим числовую последовательность: 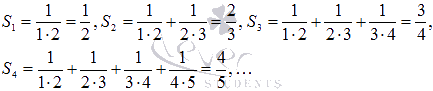 , n – произвольное натуральное число. Тогда последовательность сумм первых n элементов этой последовательности будет следующая


Исходя из этого факта, по индукции можно утверждать, что  .

Доказательство этой формулы приведем чуть ниже.

Метод математической индукции.

В основе метода математической индукции лежит принцип математической индукции.

Он заключается в следующем: некоторое утверждение справедливо для всякого натурального n, если

1. 
   оно справедливо для n = 1 и
   
2. 
   из справедливости утверждения для какого-либо произвольного натурального n = k следует его справедливость для n = k+1.
   

То есть, доказательство по методу математической индукции проводится в три этапа:

1. 
   во-первых, проверятся справедливость утверждения для любого натурального числа n (обычно проверку делают для n = 1);
   
2. 
   во-вторых, предполагается справедливость утверждения при любом натуральном n=k;
   
3. 
   в-третьих, доказывается справедливость утверждения для числа n=k+1, отталкиваясь от предположения второго пункта.
   

Примеры доказательств уравнений и неравенств методом математической индукции.

Вернемся к предыдущему примеру и докажем формулу  .

Доказательство.

Метод математической индукции предполагает доказательство в три пункта.

Поехали!

1. 
   Проверим равенство для n = 1. Имеем  . Это равенство верное.
   
2. 
   Предположим, что   есть справедливая формула.
   
3. 
   Докажем, что   отталкиваясь от справедливого равенства из второго пункта.
   

Сумма k+1 первых членов последовательности представляется как сумма первых k членов исходной числовой последовательности и k+1 ого члена:


Так как   из второго пункта, то


Осталось привести дроби к общему знаменателю, привести подобные слагаемые, воспользоваться формулой сокращенного умножения квадрат суммы и произвести сокращение: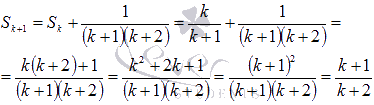


Следовательно, доказано равенство третьего пункта.

Таким образом, выполнены все три шага метода математической индукции и тем самым доказано наше предположение о формуле  .

Давайте рассмотрим тригонометрическую задачу.

Пример.

Докажите тождество  .

Решение.

Во-первых, проверяем справедливость равенства при n = 1. Для этого нам понадобятся основные формулы тригонометрии.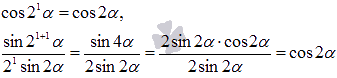


То есть, равенство верно для n = 1.

Во-вторых, предположим, что равенство верно для n = k, то есть справедливо тождество


В-третьих, переходим к доказательству равенства 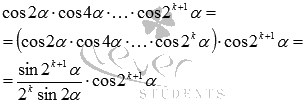  для n = k+1, основываясь на втором пункте.


Так как по формуле из тригонометрии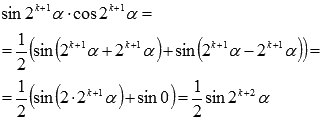
 
то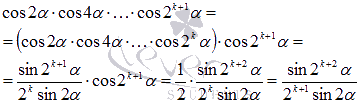


Доказательство равенства из третьего пункта завершено, следовательно, исходное тождество доказано методом математической индукции.

Формула бинома Ньютона может быть доказана методом математической индукции.

14. Сложение и умножение целых неотрицательных чисел (аксиоматический подход).

Опред: Сложением натуральных чисел называется операция (обозначается +) удовлетворяет следующим условиям:

1.(Для любого а є N) а+1= а’ , 2.(Для любых a, b є N) a+b‘ = (а+b)’ При этом результат операции называется суммой двух натуральных чисел, а компоненты– слагаемыми.

Теорема: Сумма двух натуральных чисел существует и единственна.

1.Единственность.

+, (+)

1.(Для любого а є N) а (+) 1= а’ (2)

2.(Для любых a, b є N) a (+) b = (а (+) b)’

1. (Для любого а є N) а+1= а’ (1)

2.(Для любых a, b є N) a+b = (а+b)’

Выберем элемент а М={для любого а є N | а+ b ≠ а (+) b }

1. 1єM? (a+1=a (+) 1) a+1=a’ = a (+) 1

2. b є M а + b = а (+) b=> b’ є M a+b’ = a (+)b’ а + b = а (+) b => a+b’ = a (+) b’

В силу того, что элемент а выбран произвольно следует то, что для любых а и bєN сумма а и b единственна.

2. Существование 1. a є N, М={для любого b є N | а+ b существует} (3)док-ть: M=N

док-во:

1) 1+а = а’

1 є M ? (1) (1+1=1′) – это следует из определения мн-ва натуральных чисел

(2) 1+а=(1+а)’

1+а= а’ => (1+а)’ = (а’)’ 1+а’ = (1+а)’ => (1+а)’ = 1+а’ єM

2. b єM => b’ єM a’ + b = (a+b)’ = b’+a = (b+a)’ (4)

1 єM => 1. b‘+1 = (b+1)’ = (b‘)’

2. (b‘+ а’ ) = (b‘+ а)’ b‘+ а’ = (b+ а’)’ = ((b+ а)’) = (b‘+ а)’

Вывод: 1. M=N; 2. В силу того, что а выбран произволен следует то, что для любого а и bєN сумма а и b существует.

следствия: а+1=а’ = 1+а => 1+a=a+1; a+b’=a’+b = (a+b)’

Свойства операции сложения:1.Коммуникативный закон.(Для любых чисел a, b є N) a+b = b+a 2.Ассоциативный закон.(Для любых чисел a, b, с є N) (a+b)+с = а+(b+с) 3. (Для любых чисел a, b, є N) a+b≠a или а+b≠b

Опред: Умножением натуральных чисел называется операция (обозначается «∙» ) удовлетворяет следующим условиям:

1)(Для любого а є N) а∙1= а, 2)(Для любых a, b є N) a∙b‘ =аb+a При этом результат операции называется произведением двух натуральных чисел, а компоненты– множители.

Единственность.

Свойства произведения:1. (Для любых чисел a, b є N) ab = ba2.(Для любых чисел a, b, с є N) (ab)с = а(bс)

3. .(Для любых чисел a, b, с є N) (a+b)с = ас+b

15.Натуральное число как мера величины. Арифметические действия над числами, рассматриваемыми как меры длины отрезка.

Примеры величин из начальной школы: Количество, цена, стоимость, масса, время, расстояние, длина, площадь и др. Они представляют собой особые свойства окружающих нас предметов и явлений и проявляются при сравнении предметов и явлений по этому признаку.

Измерение величин : Если задана величина А и выбрана единица измерения величины (единица величины) Е (того же рода), то измерить величину А –это значит найти такое положительное число х, что А = х ∙ Е, то есть узнать сколько раз единица измерения укладывается в измеряемой величине. Полученное число называют численным значением величины или мерой величины при выбранной единице измерения.

Численное значение величины–это число, которое показывает, сколько раз единица измерения или ее часть укладывается в измеряемой величине.

В общем виде, если А = х ∙ Е, то число х называется также мерой величины А при единице Е и пишут х = mе(А).

Виды величин:

1.Скалярная величина (определяется одним числовым значением). Пример: длина, масса.

2.Положительная скалярная величина (принимает только положительные числовые значения). Пример: длина, масса, время, стоимость, количество товара.

3.Векторная величина (характеризуется числом и направлением). Пример: скорость ветра, сила. и др.

Переход от сравнения чисел к сравнению величин и наоборот:

При выполнении операций с величинами выполняют действия с их числовыми значениями при указанной единице измерения.

1). Если величины А и В измерены при помощи единицы величины Е, то отношения между величинами А и В будут такими же, как и отношения между их числовыми значениями, и наоборот:-величины равны тогда и только тогда, когда равны их численные значения при одной и той же единице измерения. Например, 3см = 3 см, так как единицы измерения одинаковые и 3 = 3. -Величина А больше величины В тогда и только тогда, когда мера величины А больше меры величины В при одной и той же единице измерения. Например, 5 см > 3 см, так как единицы измерения одинаковые и5 > 3.-Величина А меньше величины В тогда и только тогда, когда мера величины А меньше меры величины В при одной и той же единице измерения.

Например, 5 см <7см, так как единицы измерения одинаковые и 5 <7.

2). Чтобы найти численное значение суммы величин, достаточно сложить численные значения этих величин при одной и той же единице измерения.

Например, А = 5 кг, В = 3 кг, то А + В = 5 кг + 3 кг = (5 + 3)кг = 8 кг.3). Чтобы умножить величину на число достаточно умножить на это число численное значение величины при той же единице измерения.

Например, А –2 кг, масса В в 3 раза больше массы А, то В = 3А = 3 ∙ (2 ∙ кг) = (3 ∙2) ∙кг = 6 кг.В математике при записи произведения величины А на число х принято число писать перед величиной, то есть х ∙ А.

Действия с однородными величинами:

1.Любые две однородные величины сравнимы: они либо равны, либо одна меньше другой.

Например, длина гипотенузы прямоугольного треугольника больше длины любого катета. Масса яблока меньше массы арбуза. Длины противоположных сторон прямоугольника равны.

2.Отношение «меньше» для однородных величин транзитивно:если А < В, В < С, то А < С. Например, если площадь первого треугольника меньше площади второго треугольника, а площадь второго треугольника меньше площади третьего треугольника, то площадь первого треугольника меньше площади третьего треугольника.

3.Однородные величины можно складывать, при этом получается величина того же рода.

Например, А –масса арбуза, В –масса дыни, то С = А + В –это масса арбуза и дыни. Очевидно, А + В = В + А и (А + В) + С = А + (В + С), где С –масса лимона.

4.Однородные величины можно вычитать, при этом получается величина того же рода. Например, если А =5 см, В = 3 см, 5 см –3см = (5 -3) см = 2 см5.Величину можно умножать на положительное действительное число, в результате получают величину того же рода.

Например, 5 см * 2 = (5 *2) см = 10 см6.Однородные величины можно делить, в результате получается величина другого рода, а при решении примеров –отвлеченное число.

Например, 6 см : 2 см= 6 :2= 3.

16. Теоретико-множественный подход к понятию целого неотрицательного числа.

Любому непустому конечному множеству соответствует только одно натуральное число, значит вся совокупность конечных множеств разбивается на классы равномощных множеств. В одном классе будут содержаться все одноэлементные множества, в другом все двухэлементные, и т.д. Множества одного класса различны по своей природе, но все они содержат одинаковое число элементов. И это число можно рассматривать как общее свойство класса конечных равномощных множеств. Т.о. натуральное число – это общее свойство класса конечных равномощных множеств. Нуль– общее свойство класса пустых множеств. 0 = n ( Æ ). Натуральное число а, как характеристику множества можно рассматривать с двух позиций: 1.Как число элементов в множестве А, получаемое при счете, т. е. n(А) = а и А Nа. 2.Как общее свойство класса конечных равномощных множеств.

Теоретико – множественный смысл отношений “равно” и “меньше”.

Определение

1. Числа а и b равны, если они определяются равномощными множествами. а= b Û АВ, где n(А) = а и n(B)= b. 3=3

2. а á b, если множество А равномощно собственному подмножеству множества В и а = n(А) , b = n(B). а á b Û АВ1, где В1Ì В, и В1 ¹ В, В1 ¹ Æ. 3<4 Возьмем три кружка и 4 квадрата. Круги накладываем на квадраты. Один квадрат остался незакрытым, значит, кругов меньше, чем квадратов. Поэтому можно записать так: 3<4

3.Число а меньше числа b тогда и только тогда, когда существует такое натуральное число с, что а + с = b. а á b Û $ с Î N, а + с = b. 3<4

4. Число а меньше числа b тогда и только тогда, когда отрезок натурального ряда Nа является собственным подмножеством отрезка этого ряда Nb. а á b ÛNа Ì Nb, Nа ¹ Nb. 3<4 Число 3 при счете называется раньше, чем 4. Значит 3<4.

17. Свойства множества целых неотрицательных чисел.

Теорема: во множестве целых чисел справедливо следующие свойства:

1. если λ≤>β=> λ+γ≤>β+γ

2. λ≤>β, γ>0=>λγ≤>βγ

3. λ≤>β,γ<0=> λγ≤> βγ

Это теорема о монотонности сложения и умножения.

Теорема: во множестве целых чисел выполнимо следующие условия:

1. (VλЄZ)(λ<0 либо λ=0либоλ>0

2. (Vλ,βЄZ)(λ>0,β>0=> λ+β>0, λβ>0

ас+bd> аd+bc из последней теоремы следует сто множество целых чисел линейно упорядоченное множество.

Теорема: разность 2-х целых чисел λ иβ (λ -β>0) положительно тогда и только тогда, когда λ>β.

Теорема: для любых 2-хцелых чисел (Vλ,βЄZ, β>0)( сущ-ет nЄN где λ<βn)

1. λ>0=>λ,βЄN и во мн-ве натур-х чисел аксиома Архимеда выполнена

2. λ≤0,β>0, n>0

βn>0

λ>βn

Из последней теоремы следует что множество целых чисел Архимедовски расположено.

Теорема: произведение целых чисел равно 0, λβ=0 тогда и только тогда, когда λ=0 либо β=0

Теорема: всякое целое число λ имеет соседнее число λ+1 т. е. не существует целого β, расположенного между этими числами:

1. λЄZ+, (λ+1) Є Z+, тогда обе части натуральные и теорема доказана

2. λЄZ, λ→ (-λ) установим взаимооднозначное соответствие при котором каждому отрицательному λ поставим ему число (-λ)

(-λ) ЄN

Если бы между 2-мя отрицательными числами λ-1 и λЄZ существовало некоторое отрицательное число β βЄZ, то в силу взаимооднозначности для положительных чисел (-λ)

(-λ+1) ЄN существовало бы βЄN, находящееся между ними λ-1<β<λ

-λ<-β<-λ+1 это противоречит дискретности множеству натуральных чисел.

Теорема: деление во множестве целых чисел не всегда выполнимо:

λ← (а, в) β←(с,d)

18. Отношение «равно», «меньше» и «больше» на множестве целых неотрицательных чисел.

Равномощность означает равночисленность а=в <-> АВ

Отношения равенства обладает свойствами рефлективности, симметричности и транзитивности, значит является отношением эквивалентности. Пусть А не , это значит А и В принадлежат разным классам эквивалентности и А не равно В.

Если множество А равномощно некоторому подмножеству В1 множества В, то говорят, что число а1 меньше числа В А меньше В).

(aB1, где B1
Если А меньше В, то говорят так же, что В больше А и записывают B>A

Отношение меньше обладает след свойствами:
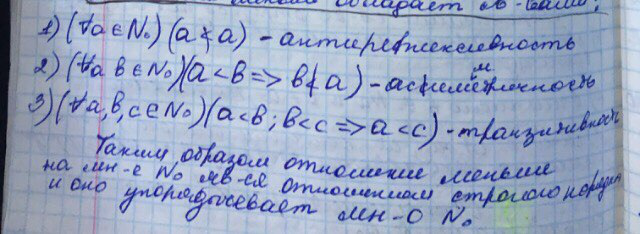
19. Сумма целых неотрицательных чисел (Задачи, определение, теорема, свойства)

Определение: Суммой целых неотрицательных чисел a и b называется целое неотрицательное число a + b, равное числу элементов в объединении непересекающихся множеств А и В, таких, что m(A) = a, m(B) = b

a + b – сумма, a и b – слагаемые.

Теорема: сумма любых двух целых неотрицательных чисел существует и она единственна.

Доказательство: Существование: пусть a и b – целые неотрицательные числа, тогда a=m(A), b=m(B), где А и В – множества любой природы и АВ=Ø. Так как А ≠Ø и В≠Ø, то АВ≠Ø и является конечным множеством =>с Z0, что с = m(AB). Тогда по определению суммы целых неотрицательных чисел с и есть сумма чисел a и b.