Ип. Документ Microsoft Office Word (7). Практическая работа 5 Операция деления чисел в эвм
 Скачать 133.32 Kb. Скачать 133.32 Kb.
|
|
Практическая работа. Операция деления чисел в ЭВМ Практическая работа №5 Операция деления чисел в ЭВМ 1. Цель работы Целью работы является изучение деления чисел как с фиксированной, так и с плавающей точкой в ЭВМ. 2. Теоретическая часть 2.1. Умножение и деление чисел в двоичной системе счисления. Ручной метод. Наиболее просто умножение выполняется в прямом коде, независимо от того, являются ли операнды целыми или дробными числами. В ЭВМ с фиксированной точкой умножение реализуется в два этапа. Первый этап заключается в определении знака произведения с помощью сложения знаковых цифр сомножителей по модулю два, где 0 – соответствует плюсу, а 1 – минусу. Таблица 2.1.1. Сложение по модулю два
По-другому, это эквивалентно 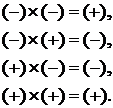 На втором этапе производится перемножение модулей сомножителей, затем в случае необходимости округления полученного модуля произведения, после чего к модулю результата приписывается его знак, определенный на первом этапе. Умножение производится по обычным правилам арифметики, согласно двоичной таблицы умножения. Рассмотрим пример: 11012 1012 11012 00002 11012 10000012 = 6510 Традиционная схема умножения похожа на известную из школьного курса процедуру записи «в столбик». Вычисление произведения двух n-разрядных двоичных чисел без знака сводится к формированию частичных произведений (ЧП) по одному на каждую цифру множителя, с последующим суммированием полученных ЧП. Перед суммированием каждое частичное произведение должно быть сдвинуто на один разряд относительно предыдущего. Студенческие работы Деление чисел в двоичной системе производится аналогично делению десятичных чисел. Рассмотрим деление двух целых чисел, так как делимое и делитель всегда могут быть приведены к такому виду путем перенесения запятой в делимом и делителе на одинаковое число разрядов и дописывания необходимых нулей. Деление начинается с того, что от делимого слева отделяется минимальная группа разрядов, которая, рассматриваемая как число, превышает или равна делителю. Дальнейшие действия выполняются по обычным правилам, прием последняя целая цифра частного получается тогда, когда все цифры делимого исчерпаны. Рассмотрим пример:  2.2. Умножение двоичных чисел в ЭВМ. Машинный метод. Умножение двоичных чисел сводится к операциям сдвига на один двоичный разряд влево и повторения первого сомножителя в тех разрядах, где второй сомножитель содержит 1, и сдвига без повторения в разрядах с 0. Сдвиг всегда чередуется со сложением, поскольку для выполнения операций имеется всего два регистра (два места для записи чисел). Другими словами, реализации отдельной операции умножения в процессоре не требуется. Как и в операции сложения, при умножении чисел с ограниченной разрядной сеткой может возникнуть переполнение. Перемножение двух n-разрядных двоичных чисел P=A*B приводит к получению результата, содержащего 2n битов. Таким образом, алгоритм умножения предполагает последовательное выполнение двух операций – сложения и сдвига. Суммирование ЧП обычно производится не на завершающем этапе, а по мере их получения. Это позволяет избежать необходимости хранения всех ЧП, то есть сокращает аппаратурные издержки. Устройство умножения предполагает наличие регистров множимого, множителя и суммы частичных произведений, а также сумматора ЧП и, возможно, схем сдвига (если операция сдвига не реализована иным способом). Существуют следующие алгоритмы умножения: 1. Алгоритм сдвига вправо - начиная с младших разрядов множителя, со сдвигом суммы ЧП вправо и при неподвижном множимом. 2. Алгоритм сдвига влево - начиная со старших разрядов множителя, со сдвигом суммы ЧП влево и неподвижном множимом. Рассмотрим пример умножения двоичных чисел в ЭВМ. Выполнить умножение чисел A = 101112 и B = 1012 в двоичной системе счисления. Умножение выполняется в несколько этапов: 1. Впишем множимое A, допустим в 8-ми разрядный регистр, начиная с младших разрядов (нумерация разрядов начинается с нуля). В недостающие разряды записываем нули. 2. Впишем множитель В в 8-ми разрядный регистр, начиная с младших разрядов. В недостающие разряды записываем нули.  3. Подготовим (обнулим) регистр результата C удвоенной разрядности (16 бит). Произведение содержит в два раза больше разрядов чем исходные сомножители. 4. Дальше выполняется следующий цикл: 4.1. Анализируем очередной разряд множителя В (начинаем с младших), если он "1", то прибавляем множимое A к старшим разрядам регистра С, результат снова в С. Если очередной разряд множителя "0", пропускаем данный шаг. 4.2. Сдвигаем содержимое регистра С на один разряд вправо. При этом крайний левый (старший) разряд заполняется нулем. Но если перед этим была операция сложения, во время которой возник перенос из старшего разряда, то тогда крайний левый разряд заполняется единицей. Канал спокойной музыки 4.3. Действия, описанные в п. п. 5.1 и 5.2,повторяютсядо тех пор не будут проанализированы все разряды множителя. В итоге процесс умножения выглядит следующим образом:  где «+А» - числоА прибавляется к регистру C; «-->»содержимое регистра C сдвигается на один разряд вправо; «=» - показывается значение частичного произведения полученного после сложения, которое заносится в регистр С. 5. Определяется знак результата. Если знаки исходных сомножителей одинаковы, то результирующее произведение положительно и наоборот. В данном случае знаки совпадают, следовательно результирующее произведение положительно. В итоге получается ответ: 2.3. Деление двоичных чисел в ЭВМ. Машинный метод. Рассмотрим процесс деления двоичных чисел в ЭВМ на примере деления числаА=100101112 на B=1012, который включает следующие этапы: 1. Впишем делимое A в 16-ти разрядный регистр, начиная с младших разрядов (нумерация разрядов начинается с нуля). В недостающие разряды записываем нули. Так как для выполнения деления требуется производить операцию вычитания, это требует использования знаковой арифметики. И поэтому в данном случае 15-й разряд является знаковым (0 - соответствует положительному числу, 1 - отрицательному), а старшим разрядом числа является 14-й разряд. 2. Впишем делитель В в 16-ти разрядный регистр, начиная с младших разрядов. В недостающие разряды записываем нули. Здесь также как и с числом A 15-й разряд является знаковым, а старшим разрядом числа является 14-й разряд. Эти знаковые разряды будут показывать нам знаки, образующихся в процессе деления, частичных остатков. Они не имеет никакого отношения к знакам исходных операндов и знаку результата, а играют чисто технологическую роль. Студенческие работы 3. Предварительный сдвиг делителя. Сдвинем делитель B влево так, чтобы позиция старшей значащей единицы, в нем, совпала с позицией старшей значащей единицы в делимом A. Количество необходимых для этого сдвигов запомним в числе k. В нашем случае старшая значащая единица в делимом Aрасположена в 7-м разряде, a в делителе B - в 2-м разряде. Следовательно, необходимо сдвинуть число B влево на 5 разрядов (k = 5). Сдвинутый делитель выглядит следующим образом : 4. Так как в процессе деления множитель B придется не только прибавлять но и вычитать, то нам необходимо иметь число -B. Для этого представим B в дополнительном коде. 5. Процесс деления будет следующий: 5.1. Вычитаем из делимого А делитель В (т. е. прибавляем -В). 5.2. Анализируем знак полученного частичного остатка (15-й разряд). В регистр результата записываем "0" если остаток отрицательный и единицу в противном случае. Помним, что отрицательному числу соответствует наличие единицы в 15-м разряде и наоборот. 5.3. Сдвигаем частичный остаток на один разряд влево. При этом крайний правый (младший) разряд заполняется нулем, а знаковый разряд (15-й) в процессе сдвига не участвует. 5.4. Прибавляем к частичному остатку делитель В если остаток отрицательный либо вычитаем делитель в противном случае. 5.5. Анализируем знак полученного частичного остатка (15-й разряд). В регистр результата записываем "0" если остаток отрицательный и единицу противном случае. 5.6. Действия, описанные в пунктах 5.3-5.5, выполняем k раз (если k=0, то ни разу не выполняем). Но, если после очередной операции сложения/вычитания частичный остаток, по модулю, будет меньше чем исходный (несдвинутый) делитель, то операция деления прекращается, а частное дополняется нулями так, чтобы число разрядов частного равнялось k+1. В итоге процесс деления для вышеуказанного примера будет выглядеть следующим образом:  где « + B» - делитель Bприбавляет к регистру делимого А; « - B» - делитель Bвычитается из регистра делимого А; «<-- » - частичный остаток сдвигается на один разряд влево; « = » - показывается значение частичного остатка полученного после сложения. 6. Определяем остаток от деления. Для этого анализируем последний частичный остаток. В нашем случае он равен "1111111110000000". 6.1.Анализируем знак остатка (15-й разряд). В знаковом разряде содержится единица, значит требуется коррекция остатка. Для коррекции прибавим к нему делитель B.  6.2. Так как в процессе деления частичные остатки были сдвинуты 5 раз влево, то для получения верного значения последний полученный остаток необходимо сдвинуть 5 раз вправо (вернуть на место). После сдвига имеем: 7. Определяем знак результата. Если знаки исходных операндов одинаковы, то результирующее частное положительно и наоборот. В данном случае знаки совпадают, следовательно результирующее частное положительно. В итоге получается ответ: 3. Задание на практическую работу Выполнить умножений и деление чисел согласно варианту задания. 4. Задачи 4.1. Выполнить деление числа C на число B в двоичной системе счисления, используя ручной метод. Показать решение. 4.2. Выполнить деление числа C на число B в двоичной системе счисления, используя машинный метод. Разрядность регистров выбрать самостоятельно. Показать решение. Таблица 4.1. Варианты заданий
|
