Диф.теңдеулер_студенттерге (копия). 1. Дифференциалды тедеу жне оны реті дегеніміз не Мысал келтірііз
 Скачать 153.16 Kb. Скачать 153.16 Kb.
|
|
І деңгей 1. Дифференциалдық теңдеу және оның реті дегеніміз не? Мысал келтіріңіз. 2. Айнымалылары ажыратылатын дифференциалдық теңдеу дегеніміз не және төмендегі теңдеулердің қайсысы айнымалылары ажыратылатын теңдеуге жатады? 1) 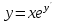 2) 2) 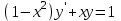 3) 3) 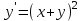 4) 4) 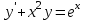 5) 5) 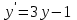 3. 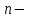 ші дәрежелі біртекті функция деген не? І ретті біртекті дифференциалдық теңдеуді шешуге қандай тәсіл қолданылады? ші дәрежелі біртекті функция деген не? І ретті біртекті дифференциалдық теңдеуді шешуге қандай тәсіл қолданылады?4. І ретті сызықтық диференциалдық теңдеу дегеніміз не? Төмендегі дифференциалдық теңдеулердің қайсысы осы теңдеуге жатады? 1) 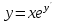 2) 2) 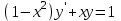 3) 3) 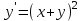 4) 4) 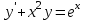 5) 5) 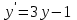 5. Реті төмендетілетін 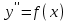 дифференциалдық теңдеулері қалай шешіледі? дифференциалдық теңдеулері қалай шешіледі? 6. Реті төмендетілетін 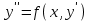 дифференциалдық теңдеулері қалай шешіледі? дифференциалдық теңдеулері қалай шешіледі?7. Реті төмендетілетін 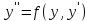 дифференциалдық теңдеулері қалай шешіледі? дифференциалдық теңдеулері қалай шешіледі?8. Характеристикалық теңдеудің түбірлері өзара тең емес болғанда ІІ ретті біртекті сызықты дифференциалдық теңдеудің жалпы шешімі қалай табылады? 9. Бернулли теңдеуін жазып, оны шығару тәсілін көрсетіңіз. 10. Толық дифференциалды теңдеу дегеніміз не және оның жалпы шешімі қалай табылады? 11. І ретті дифференциалдық теңдеудің толық дифференциалды болуының критериін тұжырымдаңыз. 12. Туындыға қатысты шешілмеген теңдеулерді шешу тәсілі. Параметр енгізу. 13. Лагранж және Клеро теңдеулері. 14. Сызықты 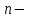 ші ретті дифференциалдық теңдеудің жалпы түрін жазыңыз. ші ретті дифференциалдық теңдеудің жалпы түрін жазыңыз.15. Сызықты біртекті дифференциалдық теңдеудің дербес шешімдерінің негізгі қасиетін тұжырымдаңыз. 16. Сызықты тәуелді және сызықты тәуелсіз функциялардың анықтамаларын беріңіз. 17. Характеристикалық теңдеудің түбірлері өзара тең болғанда ІІ ретті біртекті сызықты дифференциалдық теңдеудің жалпы шешімі қалай табылады? 18. Характеристикалық теңдеудің түбірлері комплекс сандар болғанда ІІ ретті біртекті сызықты дифференциалдық теңдеудің жалпы шешімі қалай табылады? 19. 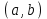 аралығында сызықты тәуелді функциялардың Вронский анықтауышы туралы теореманы тұжырымдаңыз. аралығында сызықты тәуелді функциялардың Вронский анықтауышы туралы теореманы тұжырымдаңыз.20. Жоғарғы ретті сызықты біртекті дифференциалдық теңдеудің жалпы шешімі туралы теореманы тұжырымдаңыз. 21. Жоғарғы ретті сызықты біртекті емес дифференциалдық теңдеудің жалпы шешімі туралы теореманы тұжырымдаңыз. 22. Коэффициенттері тұрақты сызықты біртекті емес дифференциалдық теңдеудің оң жағы 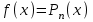 түрінде берілсе, онда оның дербес шешімі қалай табылады? түрінде берілсе, онда оның дербес шешімі қалай табылады?23. Коэффициенттері тұрақты сызықты біртекті емес дифференциалдық теңдеудің оң жағы 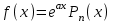 түрінде берілсе, онда оның дербес шешімі қалай табылады? түрінде берілсе, онда оның дербес шешімі қалай табылады?24. Коэффициенттері тұрақты сызықты біртекті емес дифференциалдық теңдеудің оң жағы 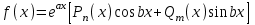 түрінде берілсе, онда оның дербес шешімі қалай табылады? түрінде берілсе, онда оның дербес шешімі қалай табылады?25. 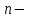 ші ретті сызықты біртекті емес дифференциалдық теңдеудің оң жағы ші ретті сызықты біртекті емес дифференциалдық теңдеудің оң жағы 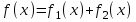 түрінде берілсе, онда оның дербес шешімі қалай табылады? түрінде берілсе, онда оның дербес шешімі қалай табылады?26. Жайдифференциалдық теңдеулер жүйесі. Жүйенің қалыпты түрі. 27. Характеристикалық теңдеудің түбірлері өзара тең емес болғанда коэффициенттері тұрақты екі біртекті сызықты дифференциалдық теңдеулер жүйесінің жалпы шешімі қалай табылады? 28. Жоғарғы ретті тұрақты коэффициентті біртекті емес теңдеулерді шешудің Лагранж (тұрақтыны вариациялау) əдісі. 29. Характеристикалық теңдеудің түбірлері өзара тең болғанда коэффициенттері тұрақты екі біртекті сызықты дифференциалдық теңдеулер жүйесінің жалпы шешімі қалай табылады? 30. Характеристикалық теңдеудің түбірлері комплекс сандар болғанда коэффициенттері тұрақты екі біртекті сызықты дифференциалдық теңдеулер жүйесінің жалпы шешімі қалай табылады? ІІ деңгей 1. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 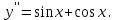 2. Дифференциалдық теңдеуді шешіңіз: 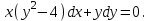 3. Теңдеудің жалпы шешімін табыңыз: а) 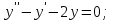 ә) ә) 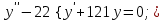 б) б) 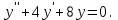 4. Дифференциалдық теңдеуді шешіңіз: 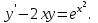 5. Теңдеудің жалпы шешімін табыңыз: а) 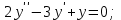 ә) ә) 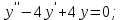 б) б) 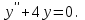 6. Дифференциалдық теңдеуді шешіңіз: 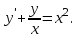 7. Дифференциалдық теңдеуді шешіңіз: 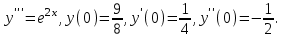 8. Дифференциалдық теңдеуді шешіңіз: 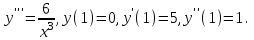 9. Дифференциалдық теңдеуді шешіңіз: 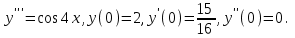 10. Дифференциалдық теңдеуді шешіңіз: 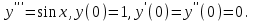 11. Теңдеудің жалпы шешімін табыңыз: а) 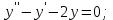 б) б) 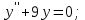 в) в) 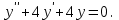 12. Теңдеудің жалпы шешімін табыңыз: а) 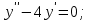 б) б) 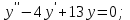 в) в) 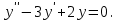 13. Теңдеудің жалпы шешімін табыңыз: а) 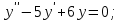 б) б) 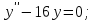 в) в) 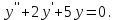 14. Теңдеуді шешіңіз: 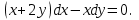 15. Теңдеуді шешіңіз: 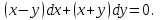 16. Теңдеуді шешіңіз: 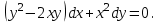 17. Теңдеуді шешіңіз: 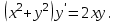 18. Теңдеуді шешіңіз: 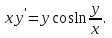 19. Теңдеуді шешіңіз: 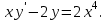 20. Теңдеуді шешіңіз: 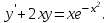 21. Теңдеуді шешіңіз: 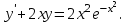 22. Теңдеуді шешіңіз: 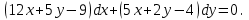 23. Теңдеуді шешіңіз: 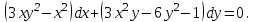 24. Теңдеуді шешіңіз: 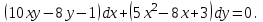 25. Теңдеуді шешіңіз: 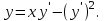 26. Теңдеуді шешіңіз: 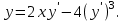 27. Теңдеуді шешіңіз: 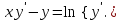 28. Теңдеуді шешіңіз: 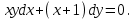 29. Теңдеуді шешіңіз: 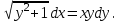 30. Теңдеуді шешіңіз: 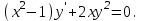 ІІІ деңгей 1. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 2. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 3. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 4. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 5. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 6. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 7. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 8. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 9. Теңдеуді шешіңіз: 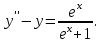 10. Теңдеуді шешіңіз: 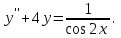 11. Теңдеуді шешіңіз: 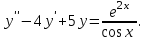 12. Теңдеуді шешіңіз: 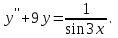 13. Теңдеуді шешіңіз: 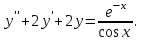 14. Дифференциалдық теңдеулер жүйесін шешіңіз: 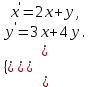 15. Дифференциалдық теңдеулер жүйесін шешіңіз: 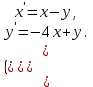 16. Дифференциалдық теңдеулер жүйесін шешіңіз: 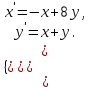 17. Дифференциалдық теңдеулер жүйесін шешіңіз: 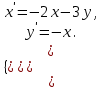 18. Дифференциалдық теңдеулер жүйесін шешіңіз: 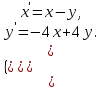 19. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 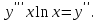 20. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 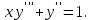 21. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 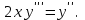 22. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 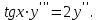 23. Дифференциалдық теңдеудің жалпы шешімін табыңыз: 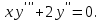 24. Коши есебін шешіңіз: 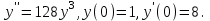 25. Коши есебін шешіңіз: 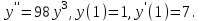 26. Коши есебін шешіңіз: 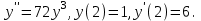 27. Коши есебін шешіңіз: 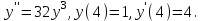 28. Коши есебін шешіңіз: 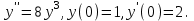 29. Дифференциалдық теңдеулер жүйесін шешіңіз: 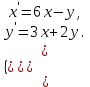 30. Теңдеуді шешіңіз: 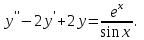
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

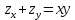
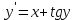
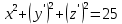
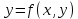
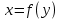
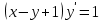
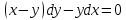
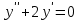
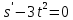
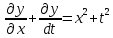
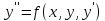 болады
болады