71. 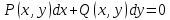 жай дифференциалдық теңдеудің интегралдаушы көбейткіші қандай жағдайда бар жай дифференциалдық теңдеудің интегралдаушы көбейткіші қандай жағдайда бар
|
1. барлық жағдайда табылады
|
2. 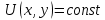 түрінде жалпы интегралы бар болғанда түрінде жалпы интегралы бар болғанда
|
3. 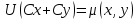 түрінде жалпы интегралы бар болғанда түрінде жалпы интегралы бар болғанда
|
4. 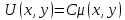 түрінде жалпы интегралы бар болғанда түрінде жалпы интегралы бар болғанда
|
5. 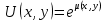 теңдігі орындалған кезде теңдігі орындалған кезде
|
72. 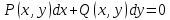 теңдеуінің тек қана теңдеуінің тек қана 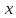 тан тәуелді интегралдаушы көбейткіші бар болса, оны қандай формуламен табуға болады тан тәуелді интегралдаушы көбейткіші бар болса, оны қандай формуламен табуға болады
|
1. 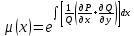
|
2. 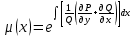
|
3. 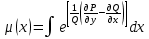
|
4. 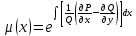
|
5. 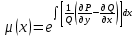
|
73. 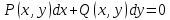 теңдеуінің тек қана теңдеуінің тек қана 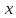 тан тәуелді интегралдаушы көбейткіші бар болса, оны қандай формуламен табуға болады тан тәуелді интегралдаушы көбейткіші бар болса, оны қандай формуламен табуға болады
|
1. 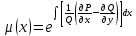
|
2. 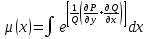
|
3. 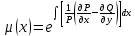
|
4. 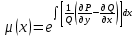
|
5. 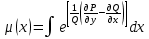
|
74. Мынадай 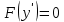 толық емес жай дифференциалдық теңдеудің жалпы интегралы қандай болады толық емес жай дифференциалдық теңдеудің жалпы интегралы қандай болады
|
1. 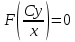
|
2. 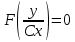
|
3. 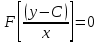
|
4. 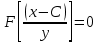
|
5. 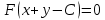
|
75. Мынадай 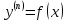 жоғарғы ретті жай дифференциалдық теңдеуді қандай әдіспен шешкен дұрыс жоғарғы ретті жай дифференциалдық теңдеуді қандай әдіспен шешкен дұрыс
|
1. параметр енгізу арқылы
|
2. біртіндеп интегралдау арқылы
|
3. біртектес теңдеуге келтіру арқылы
|
4. айнымалылардың орнын ауыстыру арқылы
|
5. бұл жай дифференциалдық теңдеу еме
|
76. Мынадай 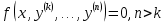 жоғарғы ретті жай дифференциалдық теңдеу берілсе, оның ретін қандай белгілеу арқылы қаншаға төмендетуге болады жоғарғы ретті жай дифференциалдық теңдеу берілсе, оның ретін қандай белгілеу арқылы қаншаға төмендетуге болады
|
1. 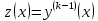 белгілеуі арқылы белгілеуі арқылы 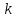 ретке төмендетуге болады ретке төмендетуге болады
|
2. 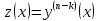 белгілеуі арқылы белгілеуі арқылы 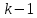 ретке төмендетуге болады ретке төмендетуге болады
|
3. 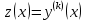 белгілеуі арқылы белгілеуі арқылы 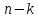 ретке төмендетуге болады ретке төмендетуге болады
|
4. 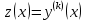 белгілеуі арқылы белгілеуі арқылы 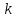 ретке төмендетуге болады ретке төмендетуге болады
|
5. 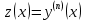 белгілеуі арқылы белгілеуі арқылы 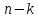 ретке төмендетуге болады ретке төмендетуге болады
|
77. Мынадай  жоғарғы ретті жай дифференциалдық теңдеу берілсе, оның ретін қандай белгілеу арқылы қаншаға төмендетуге болады жоғарғы ретті жай дифференциалдық теңдеу берілсе, оның ретін қандай белгілеу арқылы қаншаға төмендетуге болады
|
1. 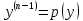 белгілеуі арқылы белгілеуі арқылы 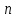 ретке төмендетуге болады ретке төмендетуге болады
|
2. 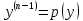 белгілеуі арқылы белгілеуі арқылы 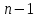 ретке төмендетуге болады ретке төмендетуге болады
|
3. 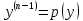 белгілеуі арқылы белгілеуі арқылы 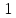 ретке төмендетуге болады ретке төмендетуге болады
|
4. 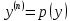 белгілеуі арқылы белгілеуі арқылы 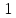 ретке төмендетуге болады ретке төмендетуге болады
|
5. 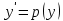 белгілеуі арқылы белгілеуі арқылы 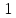 ретке төмендетуге болады ретке төмендетуге болады
|
78. 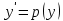 алмастыруын төмендегі жай дифференциалдық теңдеулердің қайсысының ретін төмендетуге қолданған дұрыс алмастыруын төмендегі жай дифференциалдық теңдеулердің қайсысының ретін төмендетуге қолданған дұрыс
|
1. 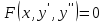
|
2. 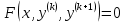
|
3. 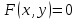
|
4. 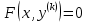
|
5. дәл жауабы жоқ
|
79. 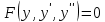 түріндегі теңдеуді бірінші ретті жай дифференциалдық теңдеуге келесі алмастырулардың қайсысы арқылы келтірген дұрыс түріндегі теңдеуді бірінші ретті жай дифференциалдық теңдеуге келесі алмастырулардың қайсысы арқылы келтірген дұрыс
|
1. 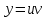
|
2. 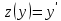
|
3. 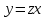
|
4. 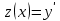
|
5. дәл жауабы жоқ
|
80. Төмендегі теңдеулердің қайсысы оң жағы біртекті функция болатын жай дифференциалдық теңдеу болады
|
1. 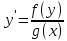
|
2. 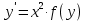
|
3. 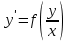
|
4. 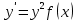
|
5. 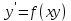
|
81. Төмендегі теңдеулердің қайсысы оң жағы біртекті функция болатын жай дифференциалдық теңдеу болады
|
1. 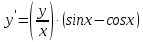
|
2. 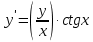
|
3. 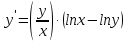
|
4. 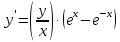
|
5. 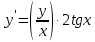
|
82. Бірінші ретті сызықтық жай дифференциалдық теңдеудің шешімін іздегенде төмендегі алмастырулардың қайсысын қолданады
|
1. 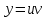
|
2. 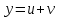
|
3. 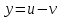
|
4. 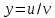
|
5. 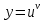
|
83. Төмедегі жай дифференциалдық теңдеулердің қайсысы сызықтық жай дифференциалдық теңдеу болады
|
1. 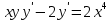
|
2. 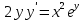
|
3. 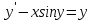
|
4. 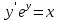
|
5. 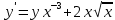
|
85. Мына дифференциалдық теңдеуді 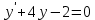 төмендегі дифференциалдық теңдеулердің қай түріне жатқызуға болады төмендегі дифференциалдық теңдеулердің қай түріне жатқызуға болады
|
1. Біртекті дифференциалдық теңдеу
|
2. Клеро теңдеуі
|
3. Екінші ретті коэффициенттері тұрақты дифференциалдық теңдеу
|
4. Бірінші ретті біртектес емес сызықтық дифференциалдық теңдеу
|
5. Бірінші ретті біртектес сызықтық дифференциалдық теңдеу
|
86. 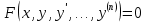 жай дифференциалдық теңдеуінің жалпы шешімінің түрін көрсетіңіз жай дифференциалдық теңдеуінің жалпы шешімінің түрін көрсетіңіз
|
1. 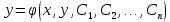
|
2. 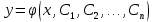
|
3. 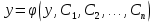
|
4. 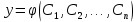
|
5. 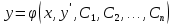
|
87. 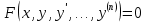 жай дифференциалдық теңдеуінің жалпы интегралының түрін көрсетіңіз жай дифференциалдық теңдеуінің жалпы интегралының түрін көрсетіңіз
|
1. 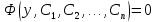
|
2. 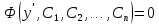
|
3. 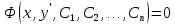
|
4. 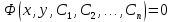
|
5. 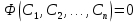
|
88. 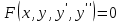 жай дифференциалдық теңдеу үшін қойылған Коши есебінде төмендегі шарттардың қайсысы бастапқы шарт бола алмайды жай дифференциалдық теңдеу үшін қойылған Коши есебінде төмендегі шарттардың қайсысы бастапқы шарт бола алмайды
|
1. 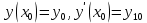
|
2. 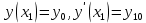
|
3. 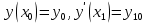
|
4. 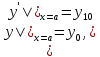
|
5. 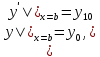
| |
 Скачать 153.16 Kb.
Скачать 153.16 Kb.