7. Төмендегі өрнектердің қайсысы екінші ретті жай дифференциалдық теңдеу болады
|
1. 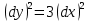
|
2. 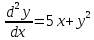
|
3. 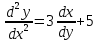
|
4. 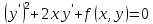
|
5. 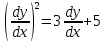
|
8. Жай дифференциалдық F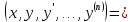 теңдеудің шешімі деп төмендегі шартты қанағаттандыратын теңдеудің шешімі деп төмендегі шартты қанағаттандыратын 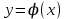 функциясын айтамыз функциясын айтамыз
|
1. Тұрақты саннан тәуелді
|
2. Туындыдан тәуелді
|
3. 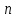 ретті үзіліссіз туындысы бар ретті үзіліссіз туындысы бар
|
4. Коши шартын қанағттандырады
|
5. Теңдеуді тепе-теңдікке айналдырады
|
9. Төмендегі функциялардың қайсысы мына теңдеудің 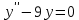 шешімі болады шешімі болады
|
1. 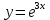
|
2. 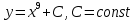
|
3. 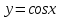
|
4. 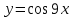
|
5. 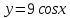
|
10. Мына дифференциалдық теңдеудің 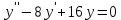 шешімі қай функция болады шешімі қай функция болады
|
1. 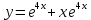
|
2. 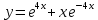
|
3. 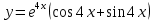
|
4. 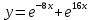
|
5. 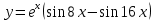
|
11. 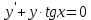 жай дифференциалдық теңдеудің жалпы шешімі келесі түрде болады жай дифференциалдық теңдеудің жалпы шешімі келесі түрде болады
|
1. 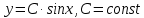
|
2. 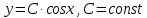
|
3. 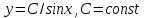
|
4. 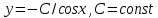
|
5. Берілген функциялардың ешқайсысы шешім болмайды
|
12. Жалпы шешімдегі тұрақты сандарға мән бергенде шығатын шешім
|
1. ерекше шешім
|
2. дербес шешім
|
3. нақты шешім
|
4. бөлекше шешім
|
5. шектелген шешім
|
13. 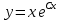 бір жай дифференциалдық теңдеудің жалпы шешімі болсын. Осы теңдеудің дербес шешімі болмайтын функцияны көрсетіңіз бір жай дифференциалдық теңдеудің жалпы шешімі болсын. Осы теңдеудің дербес шешімі болмайтын функцияны көрсетіңіз
|
1. 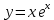
|
2. 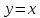
|
3. 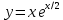
|
4. 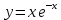
|
5. 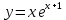
|
14. 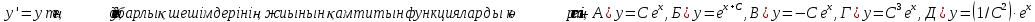
|
1. А, В, Г
|
2. А, Б
|
3. А, Б, Е
|
4. В, Г, Д
|
5. Б, В
|
15. Дифференциалдық теңдеудің жалпы шешімі белгілі болған кезде Коши есебін шешу үшін:
|
1. тұрақты сандардың мәндерін анықтау керек
|
2. жалпы шешімді теңдеуге қою керек
|
3. қосымша шарт қою қажет
|
4. біртектес теңдеуге айналдыру керек
|
5. Лагранж шартын пайдалану керек
|
16. Коши есебін шығару дегеніміз жай дифференциалдық теңдеудің
|
1. жалпы шешімін табу
|
2. жалпы интегралын табу
|
3. жалпы интегралдық сызыығын табу
|
4. шеттік шартты қанағаттандыратын дербес шешімін табу
|
5. бастапқы шартты қанағаттандыратын дербес шешімін табу
|
17. 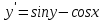 жай дифференциалдық теңдеуі үшін Коши есебінің шешімінің жалғыз болу обылысын көрсетіңіз жай дифференциалдық теңдеуі үшін Коши есебінің шешімінің жалғыз болу обылысын көрсетіңіз
|
1. 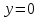 түзуінде жатпайтын түзуінде жатпайтын 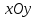 жазықтығының нүктелері жазықтығының нүктелері
|
2. 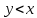 теңсіздігіне қанағаттандыратын теңсіздігіне қанағаттандыратын 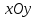 жазықтығының нүктелері жазықтығының нүктелері
|
3. 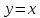 түзуінде жатпайтын түзуінде жатпайтын 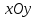 жазықтығының нүктелері жазықтығының нүктелері
|
4. 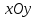 жазықтығы жазықтығы
|
5. дәл жауабы жоқ
|
18. Коши есебінде не табу керек
|
1. дифференциалдық теңдеудің жалпы шешімі
|
2. бастапқы шарт
|
3. дифференциалдық теңдеудің дербес шешімі
|
4. интегралдық сызықтар жиыны
|
5. жалпы интеграл
|
19. Дифференциалдық теңдеудің ерекше нүктесі дегеніміз
|
1. дифференциалдық теңдеуді нольге айналдыратын нүкте
|
2. Коши есебінің шешімінің бойында жатпайтын нүкте
|
3. Вронскианды нольге айналдырып жіберетін нүкте
|
4. Коши есебінің шешімінің саны біреуден көп болатын нүкте
|
5. нүктелердің бәрі бірдей, ерекше нүкте деген ұғым жоқ
|
20. Жай дифференциалдық теңдеудің ерекше шешімі дегеніміз төмендегілердің қайсысы болады
|
1. Шеттік есептің шешімі болатын шешім
|
2. Коши есебінің шектелмеген шешімі
|
3. Коши шартын қанағаттандырмайтын шешім
|
4. Жалпы шешімнен тұрақты санға мән беру арқылы алынбайтын шешім
|
5. Айқын емес түрде берілген функция арқылы өрнектелетін шешім
|
22. 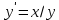 жай дифференциалдық теңдеуінің шешімдерінің жалғыз болу облысы жай дифференциалдық теңдеуінің шешімдерінің жалғыз болу облысы
|
1. дәл жауабы жоқ
|
2. 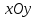 жазықтығы жазықтығы
|
3. 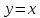 түзуінде жатпайтын түзуінде жатпайтын 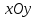 жазықтығының нүктелері жазықтығының нүктелері
|
4. 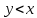 теңсіздігіне қанағаттандыратын теңсіздігіне қанағаттандыратын 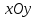 жазықтығының бөлігі жазықтығының бөлігі
|
5. 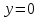 түзуінде жатпайтын түзуінде жатпайтын 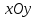 жазықтығының нүктелері жазықтығының нүктелері
|
27. 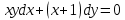 дифференциалдық теңдеуі дифференциалдық теңдеуі
|
1. айнымалылары ажыратылатын теңдеу
|
2. біртекті теңдеу
|
3. толық дифференциалды теңдеу
|
4. Бернулли теңдеуі
|
5. Клеро теңдеу
|
28. Мына теңдеу 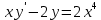
|
1. сызықтық біртекі теңдеу
|
2. коэффициенттері тұрақты теңдеу
|
3. біртекі теңдеу
|
4. сызықтық біртекті емес теңдеу
|
5. айқын түрде берілген теңдеу
|
29. Мына функциялардың қайсысы біртекті функция болады
|
1. 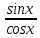
|
2. 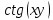
|
3. 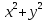
|
4. 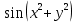
|
5. 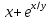
|
30. Бірінші ретті біртекті емес сызықтық жай дифференциалдық теңдеудің жалпы түрін көрсетіңіз
|
1. 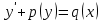
|
2. 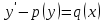
|
3. 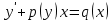
|
4. 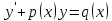
|
5. 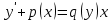
|
31. Бірінші ретті біртекті емес сызықтық жай дифференциалдық теңдеудің жалпы шешімін қай әдіспен табуға болады
|
1. дербес шешімді вариациялау арқылы
|
2. тұрақты шешімді вариациялау арқылы
|
3. тұрақты санды вариациялау арқылы
|
4. бастапқы шартты вариациялау арқылы
|
5. шеттік шартты вариациялау арқылы
| |
 Скачать 153.16 Kb.
Скачать 153.16 Kb.