Шпоры по электротехнике. 1 Электрическая цепь, элемент электрической цепи, электрическая схема

• Название: 1 Электрическая цепь, элемент электрической цепи, электрическая схема
• Анкор: Шпоры по электротехнике
• Дата: 26.02.2023
• Размер: 1.83 Mb.
• Имя файла: Shpory.docx
• Тип: Документы; #956382
• страница: 3 из 6

22)Цепь переменного тока с индуктивным элементом. Векторная диаграмма. Закон Ома в комплексной форме.

В электрических цепях переменного тока наиболее часто используют синусоидальную форму, характеризующуюся тем, что все токи и напряжения являются синусоидальными функциями времени.

 сопротивление индуктивного элемента.

Индуктивность цепи переменного тока. Инд-ть это коэф-т кот. связ. потокосцепление катушки и ток. =Li; Потокосцепл =Ф₁n₁+Ф₂n₂+…+Ф_kn_k; n_k –кол-во витков сцепленных с магнитным потоком Ф_k. ЭДС катушки при изменении потокосцепления: e= - d/dt; U_i=- e_i= d/dt= L di/dt; i=I_msin(t);

U_L=I_mLcos(t)= I_mLsin(t+/2); В комплексном виде I=I_me^j0=I_m; U=I_mLe^j/2=U_me^j/2;; Комплексное сопр. катушки индуктивности: Z=(I_mLe^j/2)/I_m=Le^j/2=Х_Le^j/2; величина Х_L=L-назыв. индуктивн. сопротивлением.

Комплекс. Плоскости: для мгновенных значений Напряж-е на индуктив-м эл-те опережает ток на угол 90

Закон Ома в компл-ном виде: I=U/Z;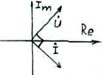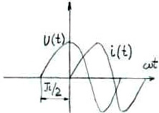



23)Соединение трехфазной цепи по схеме «звезда-звезда» с нейтральным проводом при симметричной и несимметричной нагрузках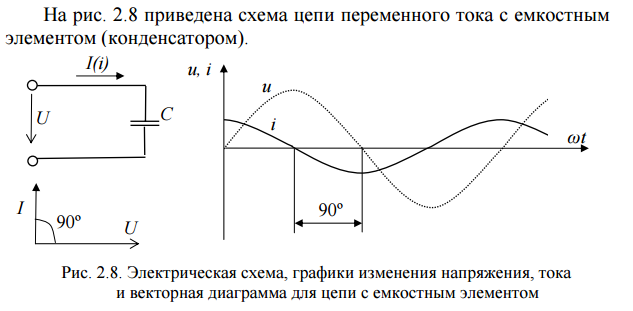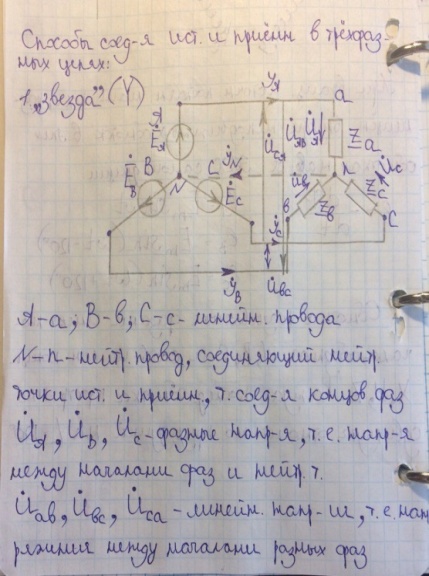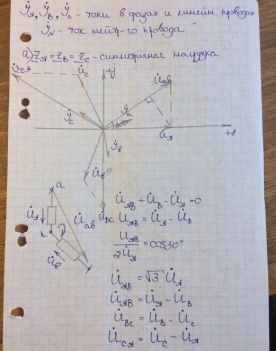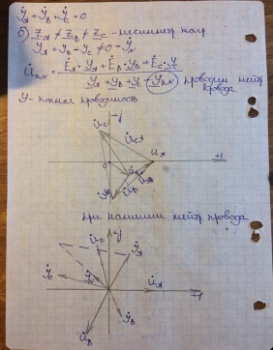

.



24)Цепь переменного тока с емкостным элементом. Векторная диаграмма. За кон Ома в комплексной форме.



25)Расчет цепи постоянного тока методом узловых потенциалов.

Метод расчета электрических цепей, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов. Число уравнений равно числу узлов в цепи. Тк любая точка схемы может быть заземлена без изменения тока распределения в ней, потенциал одного из узлов можно принять =0.

1.Обозначить в расчетной схеме все узлы. Потенциал одного из узлов принять=0.Задать произвольное направление токов

2. Составить систему уравнений по методу узл. Потенц.



Собственная проводимость узла (G_ii) представляет собой арифметическую сумму проводимостей всех ветвей, соединенных в i-м узле. Общая проводимость i-го и j-го узлов (G_ij = G_ji) представляет собой взятую со знаком «–» сумму проводимостей ветвей, присоединенных одновременно к i-му и j-му узлам. Проводимости ветвей с источниками тока полагаются равными нулю и в собственные и общие проводимости не входят! Узловой ток (J_ii) состоит из двух алгебраических сумм: первая содержит токи источников тока, содержащиеся в ветвях, соединенных в i-м узле; вторая представляет собой произведение ЭДС источников напряжения на проводимости соответствующих ветвей, соединенных в i-м узле. Со знаком «+» в эту сумму входят E и J источников, действие которых направлено к узлу, со знаком «–» – остальные.

Решение системы уравнений по методу узловых потенциалов в общем случае выполняется методом Крамера при помощи определителей. Токи в ветвях определяются по закону Ома.

26)Резонанс напряжений. Векторная диаграмма.

Состояние цепи с последовательным соединением элементов, при котором разность фаз тока и напряжения равна нулю, называется резонансом напряжений.

В этом случае нагрузка является чисто активной. При резонансе напряжений φ = 0 и U_L=U_C. Состояние резонанса напряжений возникает, если Х_L=Х_С, так как тогда I·Х_L = I·Х_С, и, следовательно U_L=U_C .

В этом случае реактивные составляющие напряжения U_L и U_C могут достигать очень больших значений, но в сумме они дают нуль.

В простейшем случае резонанс напряжений может быть получен в электрической цепи переменного тока при последовательном включении катушки индуктивности и конденсаторов. При этом, изменяя емкость конденсаторов при постоянных параметрах катушки, получают резонанс напряжений при неизменных значениях напряжения и индуктивности, частоты и активного сопротивления цепи. При изменении емкости конденсаторов С происходит изменение реактивного емкостного сопротивления. При этом полное сопротивление цепи также изменяется, следовательно, изменяются ток, коэффициент мощности, напряжения на катушке индуктивности, конденсаторах, а также активная, реактивная и полная мощности электрической цепи. Зависимости тока I, коэффициента мощности cos и полного сопротивления Z цепи переменного тока в функции емкостного сопротивления (резонансные кривые) для рассматриваемой цепи приведены на рис. 9,а. Векторная диаграмма тока и напряжений этой цепи при резонансе представлена на рис. 9,б.

Как видно из этой диаграммы, реактивная составляющая напряжения U_L на катушке при резонансе равна напряжению U_С на конденсаторе. При этом напряжение на катушке индуктивности U_к при резонансе вследствие того, что катушка кроме реактивного сопротивления X_L обладает еще и активным сопротивлением R, несколько больше, чем напряжение на конденсаторе.

Резонанс напряжений имеет ряд отличительных особенностей.

1)При резонансе напряжений полное сопротивление электрической цепи переменного тока принимает минимальное значение и оказывается равным ее активному сопротивлению, т.е.



2)Из этого следует, что при неизменном напряжении питающей сети (U= const) при резонансе напряжений ток в цепи достигает наибольшего значения I =U/Z =U/R. Теоретически ток может достигать больших значений, определяемых напряжением сети и активным сопротивлением катушки.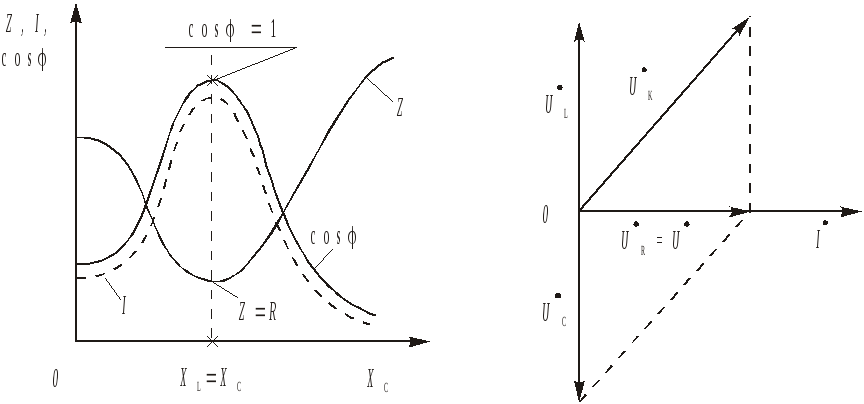



а) б)Рис. 9

3. Коэффициент мощности при резонансе cos=R/Z =R/R = 1, т.е. принимает наибольшее значение, которому соответствует угол= 0. Это означает, что вектор тока и вектор напряжения сети при этом совпадают по направлению, так как они имеют равные начальные фазы_i=_u.

4. Активная мощность при резонансе P=RI ²имеет наибольшее значение, равное полной мощности S, в то же время реактивная мощность цепи Q=XI ²= (X_LX_C)I ²оказывается равной нулю:Q =Q_LQ_C= 0.

5. При резонансе напряжений напряжения на емкости и индуктивности оказываются равными U_С=U_L=X_CI =X_LI и в зависимости от тока и реактивных сопротивлений могут принимать большие значения, во много раз превышающие напряжение питающей сети. При этом напряжение на активном сопротивлении оказывается равным напряжению питающей сети, т.е.U_R=U.

Резонанс напряжений в промышленных электротехнических установках нежелательное и опасное явление, так как оно может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или пробою изоляции обмоток электрических машин и аппаратов, изоляции кабелей и конденсаторов при возможном перенапряжении на отдельных участках цепи. В то же время резонанс напряжений широко используется в различного рода приборах и устройствах электроники

27)Цепь переменного тока с последовательным соединением элементов. Закон Ома и Кирхгофа в комплексной форме для элементов с различным х арактером нагрузки.

Рис. 2.7 Рассмотрим цепь, изображенную на рис.2.7. К этой цепи, состоящей из последовательно соединенных активного, индуктивного и емкостного элементов, подводится переменное напряжение U заданной частоты f. Рассчитаем эту цепь.

 Последовательность расчета: 1) находим полное сопротивление (импеданс) участка цепи, содержащего последовательно соединенные элементы R, L, C

(2.15)

2)находим разность фаз тока и напряжения

(2.16) Из ф ормулы (2.15) следует, что можно моделировать cопротивление цепи в виде треугольника, у которого катеты равны R и (Х_L-Х_С), а гипотенуза равна полному сопротивлению Z.

«Треугольник сопротивлений»: Угол между катетом R и гипотенузой Z соответствует разности фаз φ.

tgφ =   (2.17)

Из формулы (2.16) следуют частные случаи: разность фаз тока и напряжения:

на активном элементе φ_R = 0; на идеальном индуктивном элементе φ_L= 90⁰ ; на емкостном элементе φ_C= -90⁰. 3) находим ток в цепи, используя закон Ома : I=

4) находим напряжения на отдельных элементах, также применяя закон Ома:

U_R =I ; U_L=I  ; U_C=I .

Примечание: Реальный индуктивный элемент является частным случаем рассмотренной выше цепи (последовательное соединение R и L, Х_С=0)

В цепях переменного тока закон Ома выражается совокупностью соотношений:

I =   (а)

(2.18)

(б)

Соотношение (б) определяет разность фаз U и I.

Закон Ома и Кирхгофа в комплексной форме для элементов с различным характером нагрузки.

Выражения закона Ома в комплексной форме имеют вид:                                                             

Достоинство этих выражений заключается в том, что в них учитывается как связь между действующими током   и напряжением  , так и сдвиг фаз φ между ними.

П ервый закон Кирхгофа в применении к узлу цепи, для мгновенных токов имеющий вид  , в комплексной форме записывается в виде

т.е. сумма комплексных токов, направленных к узлу, равна сумме комплексных токов, направленных от него, т.е. алгебраическая сумма комплексных токов в узле равна 0.

Второй закон Кирхгофав применении к контуру цепи, для мгновенных ЭДС и падений напряжений имеющий вид  , в комплексной форме записывается в виде

                                                  (2.17)

где  - комплексные ЭДС, падение напряжения, ток и сопротивление в k-й ветви, входящей в контур. Для всякого замкнутого контура алгебраическая сумма комплексных ЭДС источников питания равна алгебраической сумме комплексных падений напряжений. Если в ветвь входят последовательно соединенные участок с сопротивлением r_k, катушка с индуктивностью L_k и конденсатор с емкостью C_k, то

   или   

для этой ветви имеем:



Как было указано выше, необходимо перед составлением уравнений по законам Кирхгофа задать положительные направления ЭДС, токов и напряжений во всех ветвях цепи, обозначив эти направления на схеме стрелками. В этом отношении полезным может оказаться обозначение ЭДС, токов и напряжений двойными индексами, соответствующими обозначению узлов, между которыми находится данная ветвь цепи. Достаточно условиться, что положительное направление принимается от узла, соответствующего первому индексу, к узлу, соответствующему второму индексу, и тогда уже нет необходимости ставить стрелки на схеме, а сама аналитическая запись величин указывает принятое их положительное направление. При изменении порядка расположения индексов меняется знак ЭДС, тока или напряжения. Так как сопротивления ветвей цепи и проводимости являются параметрами, не имеющими направления, то порядок индексов у них безразличен.

Все эти правила действуют и при использовании комплексного метода, т.е. имеют место соотношения:

           

28)Мощность цепи синусоидального тока (мгновенное, активное, реактивное, полное). Коэффициент мощности.

Произведение мгновенных значений напряжения и тока в цепи называют мгновенной мощностью, т.е.



Активная мощность.

Единица измерения — ватт (W, Вт).

Среднее за период T значение мгновенной мощности называется активной мощностью:  Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле P=I²∙r=U²∙g.

Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную)

Реактивная мощность. Единица измерения — вольт-ампер реактивный (var, вар).

Р еактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряженияU и тока I, умноженному на синус угла сдвига фаз φ между ними:   (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением:  .

Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.

Полная мощность.

Единица полной электрической мощности — вольт-ампер (V·A, В·А)

П 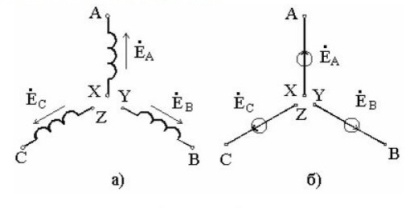олная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: S = U·I; связана с активной и реактивной мощностями соотношением: S= , где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0). Векторная зависимость между полной, активной и реактивной мощностью выражается формулой: 

Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии.

Коэффициент мощности

  Коэффициент мощности показывает какую часть полной мощности составляет активная мощность.  Чем больше , тем больше активная мощность.