Шпоры по электротехнике. 1 Электрическая цепь, элемент электрической цепи, электрическая схема
 Скачать 1.83 Mb.
|
|
12)Понятие о резонансе напряжений. Векторная диаграмма. Резонанс – такой режим работы элементов цепи, при котором она ведет себя, по отношению к источнику энергии, как чисто активное сопротивление, т.е. напряжение и ток совпадают по фазе.  Резонанс напряжения: z1=R; z2=jL=jXL; z3=-j/c=-jXC; z=z1+z2+z3=R+jXL-jXC=R+j(XL-XC); XL=XC – условие резонанса напряжения. L=1/C; 0=1/(LC) – резонансная частота. Сопротивление любого реактивного элемента по резонансной частоте называется характеристическим сопротивлением последовательного колебания контура. =0L=1/0C=(L/C). Добротностью контура называется отношение характеристического сопротивления контура к его активному сопротивлению: q=/R. Резонанс напряжения характеризуется следующим: 1. Ток в режиме резонанса maх: Iрез=U/Z =U/R; 2. Напряжения на реактивных элементах возрастают в q-раз по отношению к напряжению источника питания: UL=XLIрез; UC=XCIрез; UL=UC; U  R+UL+UC=IрезR+IрезjXL+Iрез(-jXC)=IрезR+Iрезj(XL-XC)=IрезR; UL/U=UC/U=Iрез/RIрез=/R=q. 3. Реактив. мощность QL u QC равны между собой, а активная мощность максимальная. P=I2резR; Q=QL-QC=I2резXL-I2резXC=I2рез(XL-XC)=0; Реактив мощность, потребляемая контуром, равна 0. Векторная диаграмма – совокупность векторов комплексных значений синусоидальных величин. UL=UC; QC=QL; Cos(φ)=1 – коэффициент мощности. 13)Законы Кирхгофа. Расчет линейных цепей постоянного тока методом узловых потенциалов. Первый закон Кирхгофа - алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла. Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда. Второй закон Кирхгофа - алгебраическая сумма напряжений на резистивных элементах замкнутого контура, равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю: Метод узловых потенциалов. Сущность метода – определение потенциалов узлов электрической цепи и дальнейшее вычисление токов в ветвях применяя закон Ома. Неизвестными в уравнениях являются потенциалы узлов, а количество уравнений определяется количеством узлов в цепи, т.к. точка схемы может быть замещена. Один из узлов схемы можно мысленно заделить, т.е. принять его потенциал равным нулю, что позволяет уменьшить число неизвестных и количество уравнений. 14)Полупроводниковые диоды. Типы диодов. Вольт-амперная характеристика. Полупроводниковый электрический диод или диодный вентиль – это устройство, которое выполнено из полупроводниковых материалов (как правило, из кремния) и работает только с односторонним потоком заряженных частиц. Основным компонентом является кристаллическая часть, с p-n переходом, которая подключена к двум электрическими контактами. Трубки вакуумного диода имеют два электрода: пластину (анод) и нагретый катод. Типы диодов: 1)выпрямительные-это электродный элемент, к-ый имеет 2 электрода (анод и катод), в к-ом реализуются свойства p-n перехода.  2)стабилитроны- используют обратную ветвь характеристики диода с обратимым пробоем для стабилизации напряжения  3)тунельные- Диоды, существенно использующие квантово – механические эффекты. Имеют область т.н. “отрицательного сопротивления” на вольт – амперной характеристике. Применяют как усилители, генератора  4)обращенные-  5)варикапы- применяются в качестве конденсаторов переменной ёмкости  Вольт-амперная характеристика выражает зависимость тока, проходящего через диод, от величины и полярности приложенного к нему постоянного напряжения. «Прямая» ветвь, изображаемая в правом верхнем квадранте‚ соответствует пропускному направлению тока, а «обратная» ветвь (в левом нижнем квадранте) – запорному. Чем круче и ближе к вертикальной оси поднимается прямая ветвь и чем ближе к горизонтальной оси и на большем ее протяжении прилегает к ней обратная ветвь, тем лучше диод. Требованиям‚ предъявляемым к прямой ветви, лучше всего удовлетворяют германиевые плоскостные диоды, а обратная ветвь лучше у кремниевых диодов. 15)Получение синусоидальной ЭДС. Закон электромагнитной индукции. Основные величины, характеризующие синусоидальные функции времени. Для получения ЭДС синусоидальной формы применяется генератор переменного тока. Однако для изучения принципа получения синусоидального переменного тока генератор можно заменить, проводником в виде прямоугольной рамки который вращают в равномерном магнитном поле с постоянной частотой. (рис. 12.1). Закон электромагнитной индукции 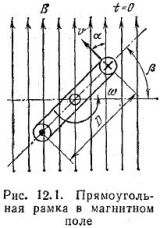 Электродвижущая сила, индуцируемая в проводящем контуре, равна скорости изменения магнитного потока, сцепляющегося с этим контуром.  В катушке, которая имеет несколько витков, общая ЭДС зависит от количества витков n:  Но в общем случае, применяют формулу ЭДС с общим потокосцеплением:  ЭДС возбуждаемая в контуре, создает ток. Наиболее простым примером появления тока в проводнике является катушка, через которую проходит постоянный магнит. Основные величины, характеризующие синусоидальные функции времени Переменный ток (ЭДС, напряжение) может изменяться во времени как по периодическому, так и по непериодическому закону. Наиболее широко используется периодический ток (ЭДС, напряжение) изменяющийся по синусоидальному закону. Такой ток характеризуется периодом Т – минимальным интервалом времени поистечении которого значения тока повторяются. Период измеряется в секундах. Величина, обратная периоду, т.е. число полных изменений периодической величины за 1 с, называется частотой. 16)Понятие о резонансе токов. Векторная диаграмма. Резонанс токов возникает в электрических цепях переменного тока при параллельном соединении ветвей с разнохарактерными (индуктивными и емкостными) реактивными сопротивлениями. В режиме резонанса токов реактивная индуктивная проводимость цепи оказывается равной ее реактивной емкостной проводимости, т.е. BL=BC. Простейшей электрической цепью, в которой может наблюдаться резонанс токов, является цепь с параллельным соединением катушки индуктивности и конденсатора . 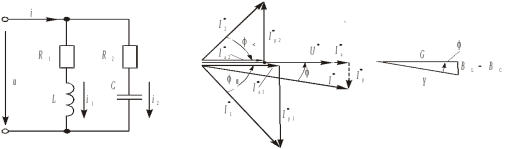 Простейшие резонансные цепи, состоящие из параллельно соединенных между собой катушки индуктивности и конденсатора, широко применяются в радиоэлектронике в качестве колебательных контуров, резонанс токов в которых достигается при некоторой определенной частоте поступающего на вход соответствующего устройства сигнала. Резонанс токов характеризуется следующими явлениями: 1) При резонансе токов полная проводимость всей электрической цепи приобретает минимальное значение и становится равной активной ее составляющей: Y =  =G; 2) Минимальное значение проводимости обусловливает минимальное значение тока цепи: I = YU = GU; 3) Емкостный ток ICи индуктивная составляющая IL тока катушки Iк оказываются при этом равными по величине, а активная составляющая тока катушки Iа1 становится равной току I, потребляемому из сети; 4) Реактивная составляющая полной мощности цепи при BL=BC оказывается равной нулю; 5) Полная мощность цепи при резонансе равна ее активной составляющей; 6) Коэффициент мощности всей цепи при резонансе cosα = P/S=1. Векторной диаграммой называется совокупность векторов ЭДС, напряжений и токов, изображённых в одной системе координат. Наиболее распространённым типом векторной диаграммы является диаграмма, которая содержит на комплексной плоскости комплексы действующих значений ЭДС, напряжений и токов. 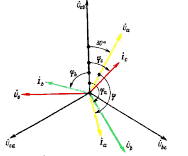 17)Представление синусоидальных функций в различных формах. Аналитическая форма представления I = Im·sin(ω·t + ψi), u = Um·sin(ω·t + ψu), e = Em·sin(ω·t + ψe), где I, u, e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени; Im, Um, Em – амплитуды синусоидального тока, напряжения, ЭДС; (ω·t + ψ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы; ψi, ψu, ψe – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0). Начальная фаза может иметь как положительное так и отрицательное значение. Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω = 2πf. Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины. Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 3.2 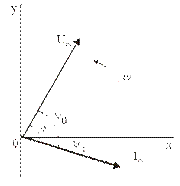 Рис. 3.2 – Представление синусоидального напряжения и тока векторной диаграммой в момент времени t=0 Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей. Ток и напряжение изобразим в виде векторов на комплексной плоскости, рис. 3.3. Ось абсцисс называют осью действительных чисел и обозначают +1, ось ординат называют осью мнимых чисел и обозначают +j. (В некоторых учебниках ось действительных чисел обозначают Re, а ось мнимых – Im). 18)Биполярные транзисторы. Устройство. Принцип действия. Параметры транзисторов. Обозначения в схемах. Применение. Биполярный транзистор - электронный полупроводниковый прибор, один из типов транзисторов, предназначенный для усиления, генерирования и преобразования электрических сигналов. Транзистор называется биполярный, поскольку в работе прибора одновременно участвуют два типа носителей заряда – электроны и дырки. Этим он отличается от униполярного(полевого) транзистора, в работе которого участвует только один тип носителей заряда. Устройство. Биполярный транзистор состоит из трех слоев полупроводника и двух PN-переходов. Различают PNP и NPN транзисторы по типу чередования дырочной и электронной проводимостей. Это похоже на два диода, соединенных лицом к лицу или наоборот. У биполярного транзистора три контакта (электрода). Контакт, выходящий из центрального слоя, называется база. Крайние электроды носят названия коллектор и эмиттер. Прослойка базы очень тонкая относительно коллектора и эмиттера. В дополнение к этому, области полупроводников по краям транзистора несимметричны. Слой полупроводника со стороны коллектора немного толще, чем со стороны эмиттера. Это необходимо для правильной работы транзистора.  19)Цепь переменного тока с резистором. Векторная диаграмма. Закон Ома в комплексной форме. Когда в электрическую цепь переменного тока подключается активное сопротивление R, то под воздействием разницы потенциалов источника в цепи начинает течь ток I. В тех случаях, когда изменение напряжения происходит по синусоидальному закону, который выражается, как u = Um sin ωt, то изменение тока i также идет по синусоиде: Активное сопротивление Т  ак что получается, что изменение напряжения и тока происходят по одинаковым законам. При этом через нулевое значение они проходят одновременно и своих максимальных значений также достигают одновременно. Из этого следует, что когда в электрическую цепь переменного тока подключается активное сопротивление R, то напряжение и ток совпадают по фазе.Е  сли к резистивному элементу приложено синусоид напряж, то по з-ну Ома для мгнов знач i=u/R= Umsin(t+u)/R. => ток измен по синусоид з-ну. Нач фаза тока i =u, => сдвиг фаз =u-i =0, т.е напряж и ток совп по фазе. З. Ома в комплексной форме I = U/Z, Z - комплексное сопротивление - отношения комплекса падения напряжения на элементе к комплексу тока, протекающего ч/з элемент.  Векторная диаграмма - это графическое изображение векторов токов и напряжений в пели на комплексной плоскости . Диаграмму рисуют относительно комплексных амплитуд (либо комплексов действующих значений) - см.рис.2.11  Рис 2 11 Векторная временные зависимости тока диатрамма ветви с активным и напряжения в ветви с активным сопротивлением сопротивлением 20)Потери энергии в трансформаторах. Энергетическая диаграмма трансформатора. КПД трансформатора. П  отери активной и реактивной мощности в трансформаторах и автотрансформаторах разделяются на потери в стали и потери в меди (нагрузочные потери). Потери в стали – это потери в проводимостях трансформаторов. Они зависят от приложенного напряжения. Нагрузочные потери – это потери в сопротивлениях трансформаторов. Они зависят от тока нагрузки.(рис)21)Символический (комплексный) метод расчета цепей синусоидального тока при включении элементов с различным характером нагрузки. Сущность символического (комплексного) метода расчета цепей синусоидального тока состоит в том, что все известные напряжения и токи, а также элементы цепи заменяются их изображениями в комплексной форме, т. е. напряжения и токи заменяются комплексами их действующих значений, элементы цепи – их комплексными сопротивлениями. Синусоидальный ток i(t) = Im sin(ωt + ψ) можно представить комплексным числом Ím на комплексной плоскости Ím = Imejψ, где амплитуда тока Im – модуль, а угол ψ, являющийся начальной фазой, – аргумент комплексного тока.  Использование комплексной формы представления позволяет заменить геометрические операции над векторами алгебраическими операциями над комплексными числами. В результате этого к анализу цепей переменного тока могут быть применены все методы анализа цепей постоянного тока |