МАИОС. МАОС без 1 главы (офворд 2003). 1. фильтрация сигналов на фоне помех

• Название: 1. фильтрация сигналов на фоне помех
• Анкор: МАИОС
• Дата: 27.02.2022
• Размер: 1.91 Mb.
• Имя файла: МАОС без 1 главы (офворд 2003).doc
• Тип: Документы; #375573
• страница: 12 из 19

2.7. Обнаружение сигнала со случайной начальной фазой

Рассмотрим обнаружение сигнала, имеющего детерминированную амплитуду и случайную начальную фазу высокочастотного заполнения. Будем считать, что плотность распределения вероятностей фазы равномерна в интервале 0...2: p()= 1/2 .

Отношение правдоподобия в этом случае будет еще и функцией фазы . Энергия сигнала мало зависит от , поэтому считаем ее постоянной.

Пусть полезный сигнал имеет вид:



где A(t) – детерминированный амплитудный множитель; (t) – детерминированный фазовый множитель; b – случайный фазовый множитель.

Тогда выражение для корреляционного интеграла будет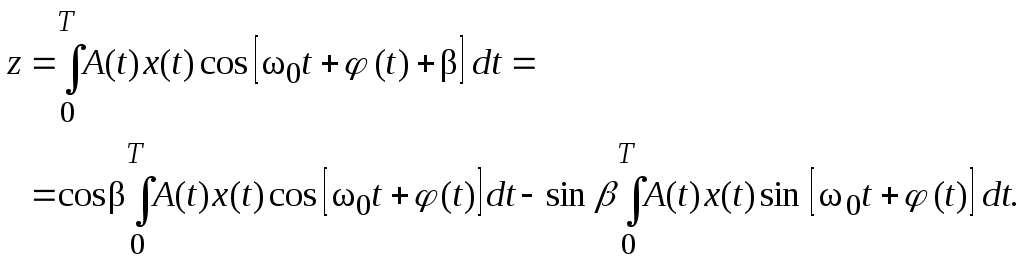




Введем обозначения:

.

Тогда . Найдем огибающую Z и фазу q корреляционного интеграла: . Тогда корреляционный интеграл запишется в виде

,

где

Подставим эту формулу в выражение (2.14) для отношения правдоподобия полностью известного сигнала:

.

Это выражение является случайной функцией b. Поэтому в нем необходимо произвести усреднение по b. Тогда

.

Но, по определению,

,

где I₀(x) – модифицированная функция Бесселя нулевого порядка. Окончательно

.

Это отношение правдоподобия является монотонной функцией огибающей корреляционного сигнала Z. Поэтому оптимальным правилом обнаружения является вычисление значения Z и сравнение его с порогом Z₀. Если Z > Z₀ , сигнал есть, если Z < Z₀ , сигнала нет. Структурная схема обнаружителя, включающая два квадратурных канала, представлена на рис. 2.9.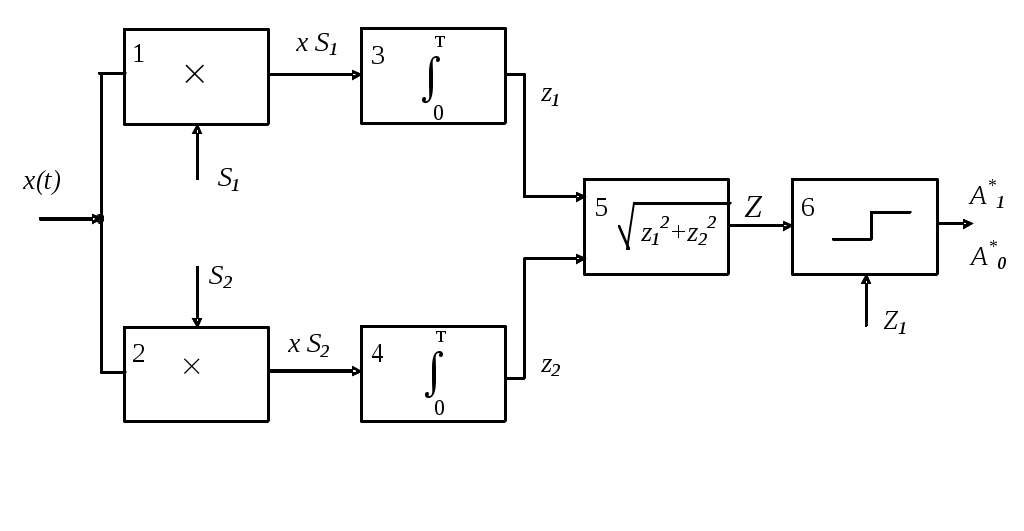


Рис. 2.9
В каждом канале вычисляются квадратурные составляющие корреляционного интеграла z₁ и z₂ соответственно. Затем находится огибающая Z, которая сравнивается с порогом Z₀, устанавливаемым в соответствии с выбранным критерием оптимальности.

В качестве опорных напряжений для умножителей используются сдвинутые по фазе на  /2 колебания высокой частоты:

.

Для расчета кривых обнаружения необходимо найти законы распределения величины Z при наличии и отсутствии сигнала. Случайные величины z₁ и z₂ не коррелированы и распределены по гауссовскому закону. Тогда при отсутствии сигнала на входе плотность распределения вероятностей Z описывается законом Рэлея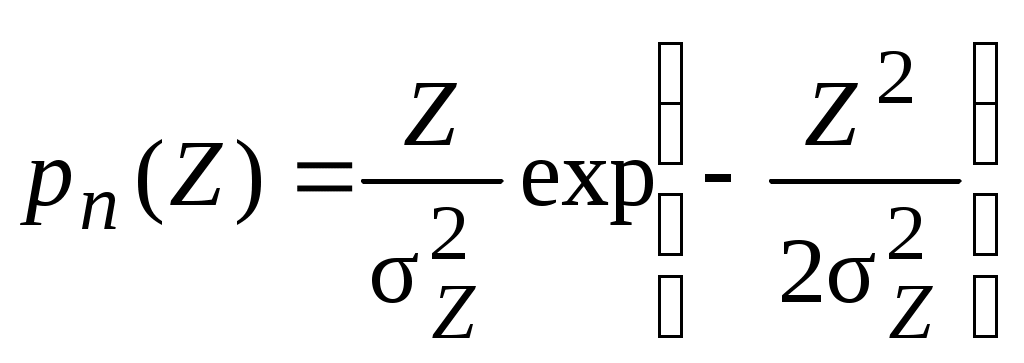

.

При наличии сигнала на входе плотность распределения вероятностей Z описывается обобщенным законом Рэлея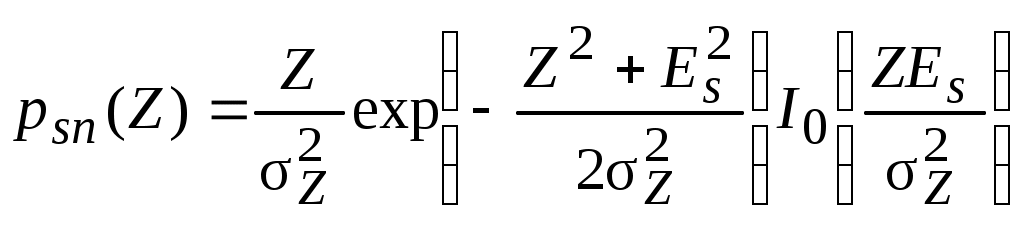

.

Из теории распределения Рэлея известно, что

.

Тогда условная вероятность ложной тревоги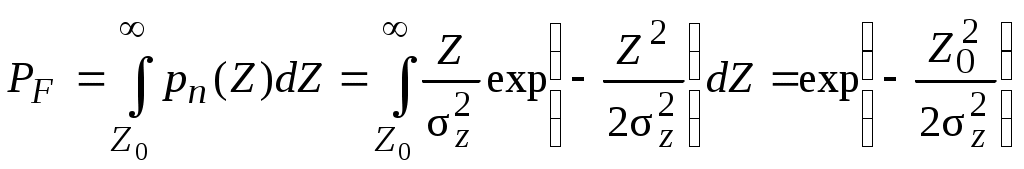

. (2.17)

При работе обнаружителя по критерию Неймана-Пирсона из выражения (2.17) может быть определен порог регистрации :



Условная вероятность правильного обнаружения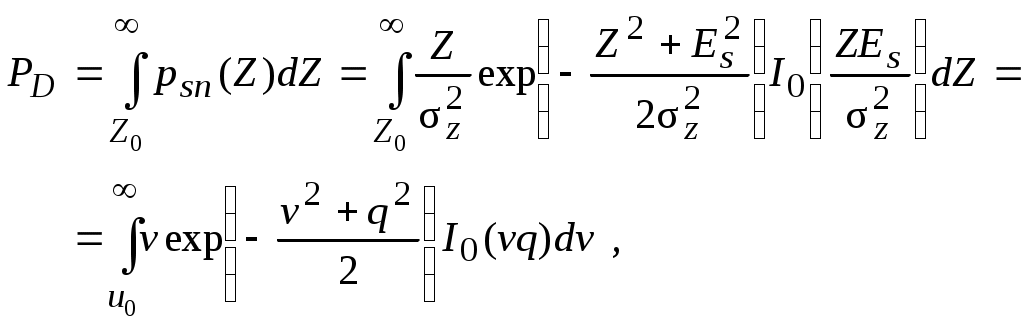

_(2.18)

где .

Определяемая отсюда величина условной вероятности правильного обнаружения P_D может быть найдена по таблицам функции распределения обобщенного закона Рэлея (закона Рэлея-Райса) либо численным интегрированием. Результаты расчетов по выражениям (2.17) и (2.18) приведены на рис. 2.6 (штриховые линии). Примерная картина плотностей распределения на входе порогового устройства приведена на рис. 2.10.

Р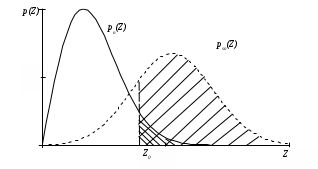
ис. 2.10
Значительно проще структурная схема оптимального обнаружителя с согласованным фильтром (рис. 2.11):

Рис. 2.11

Она состоит из согласованного фильтра 1, детектора огибающей 2 и порогового устройства 3. Детектор выполняет функцию выделения огибающей. Характеристики обнаружения такого обнаружителя могут быть определены по формулам (2.17) и (2.18).