МАИОС. МАОС без 1 главы (офворд 2003). 1. фильтрация сигналов на фоне помех

• Название: 1. фильтрация сигналов на фоне помех
• Анкор: МАИОС
• Дата: 27.02.2022
• Размер: 1.91 Mb.
• Имя файла: МАОС без 1 главы (офворд 2003).doc
• Тип: Документы; #375573
• страница: 8 из 19

2. ОСНОВЫ ТЕОРИИ ОБНАРУЖЕНИЯ СИГНАЛОВ

НА ФОНЕ ПОМЕХ

2. 1. Постановка задачи

Обнаружение сигналов практически всегда происходит при необходимости установить факт наличия или отсутствия какого-либо определенного физического объекта. Однако непосредственно установить этот факт мы обычно не можем, а можем лишь воспользоваться тем, что наличие или отсутствие интересующего нас объекта изменяет те или иные параметры некоторого сигнала – амплитуду (или сам факт наличия сигнала), время прихода, частоту, фазу и т. п. Примером может служить сигнал эхо-локационной системы, отраженный от какого-либо объекта. В этом случае сигнал присутствует лишь при наличии объекта. В других случаях объект только изменяет параметры сигнала, который присутствует все время. Общим во всех этих ситуациях является то, что сигнал поступает всегда вместе с помехами, а это может привести к ошибочным решениям. Случайный характер как помех, так и полезных сигналов приводит к тому, что при решении задачи обнаружения следует исходить из положений теории статистических решений.

2.2. Метод статистических решений

Пусть факт наличия или отсутствия сигнала s(t,) в принятом колебании x(t) неизвестен [5]. Тогда можно записать:

(2.1)

где Q – случайная величина, могущая принимать лишь два значения: Q = 0 (сигнал отсутствует) и Q = 1(сигнал присутствует). По принятой конкретной реализации x(t) на интервале T нужно оптимальным образом решить, присутствует или отсутствует полезный сигнал s(t, ). Иначе говоря, нужно оценить значение дискретного параметра Q . В результате решения задачи нужно получить структурную схему оптимального обнаружителя и определить количественные характеристики его работы. Задачи такого рода часто называются задачами бинарного обнаружения, поскольку имеются лишь две альтернативы: либо сигнал (и соответственно объект, его порождающий) присутствует, либо он отсутствует.



Рис. 2.1
Пусть в результате проведения некоторого опыта значения x_i случайной функции X попадают в область Г (рис. 2.1) [8]. Опыт производится для проверки гипотезы Н₀ (нулевая гипотеза) о том, что случайная функция имеет плотность распределения вероятностей p₀(x) . Альтернативной является гипотеза Н₁ о том, что случайная функция имеет плотность распределения p₁(x).

Для принятия решения нужно сначала установить некоторый критерий или правило решения, т. е. каждому x_i из области Гпоставить в соответствие либо гипотезу Н₀ , либо гипотезу Н₁ , иначе говоря, разбить область Гна две части: Г₀иГ₁, причем для x, попадающих в подобласть Г_0, считать справедливой гипотезу Н₀ , а для x, попадающих в подобласть Г₁ – гипотезу Н₁ . Так как решение должно быть однозначным, то возможны ошибки.

Ошибка первого рода состоит в том, что гипотеза Н₀ отвергается, когда она на самом деле верна (принимается решение Н = Н₁, когда на самом деле Н = Н₀).

Ошибка второго рода состоит в том, что гипотеза Н₀ принимается, хотя на самом деле она является ложной (принимается решение Н = Н₀, когда на самом деле Н = Н₁) .

Пусть p₀(x) = p(x|Н₀) – плотность распределения вероятностей результатов опыта при условии, что верна гипотеза Н₀ . Тогда условная вероятность ошибки первого рода

(2.2)

Она определяется вероятностью попадания точек x_i в подобласть Г₁ при условии, что справедлив закон распределения p₀(x).

Аналогично, условная вероятность ошибки второго рода

, (2.3)

где , а условная вероятность правильного решения, состоящего в том, что гипотеза Н₀ отвергается, а принимается гипотеза Н₁, определяется выражением



Условная вероятность правильного решения относительно выбора гипотезы Н₁ называется мощностью критерия (или мощностью решающего правила). Чем больше мощность критерия, тем лучше решение.

Очевидно, что оптимальный критерий (правило решения) должен тем или иным образом уменьшать ошибки решения.

Пусть плотность распределения вероятностей n-мерной выборки исследуемой случайной функции при условии, что верна гипотеза Н₀, известна и равна Аналогично, плотность распределения вероятностей при условии, что верна гипотеза Н₁ , равна Тогда можно ввести отношение плотностей распределения

(2.4)

Это отношение называют отношением правдоподобия. Критерии, применяемые при проверке гипотез, обычно базируются на сравнении отношения правдоподобия с некоторым порогом l₀ :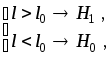

(2.5)

т. е. если l> l₀ , принимается решение о справедливости гипотезы Н₁, а если l<l₀, принимается гипотеза Н₀. Задача сводится к оптимальному выбору критического или порогового значения l₀.