1. 7. Фильтрация сигнала на фоне реверберационной помехи
Спектральная плотность реверберационной помехи в каждый момент времени с точностью до постоянного множителя совпадает со спектральной плотностью зондирующего сигнала:
 , ,
где 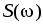 – спектральная плотность зондирующего сигнала; а – коэффициент пропорциональности. – спектральная плотность зондирующего сигнала; а – коэффициент пропорциональности.
С другой стороны, можно считать, что амплитудный спектр  ) сигнала, отраженного от дефекта, также пропорционален амплитудному спектру зондирующего сигнала ) сигнала, отраженного от дефекта, также пропорционален амплитудному спектру зондирующего сигнала  ): ):
 , ,
где k – коэффициент пропорциональности, учитывающий коэффициент отражения от выявляемого объекта и ослабление амплитуды сигнала при его распространении; 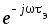 – множитель, учитывающий задержку сигнала при его распространении; tэ= 2r/ c ; r – расстояние до отражателя; c – скорость распространения сигнала. – множитель, учитывающий задержку сигнала при его распространении; tэ= 2r/ c ; r – расстояние до отражателя; c – скорость распространения сигнала.
Тогда на основе формулы (1.8) можно записать выражение для частотной характеристики оптимального фильтра обнаружения эхо-сигнала на фоне реверберационной помехи:
 (1.21) (1.21)
Фильтр, комплексная частотная характеристика которого определяется формулой (1.21), называется обратным фильтром или фильтром Урковица. Видно, что фильтрация здесь затруднена, так как она осуществляется за счет подавления спектра сигнала.
На практике реверберационная помеха действует вместе с некоррелированной с сигналом шумовой помехой, имеющей спектральную плотность N0/2 в полосе частот  . В этом случае спектральная плотность помехи . В этом случае спектральная плотность помехи

Тогда можно получить выражение для частотной характеристики оптимального фильтра:
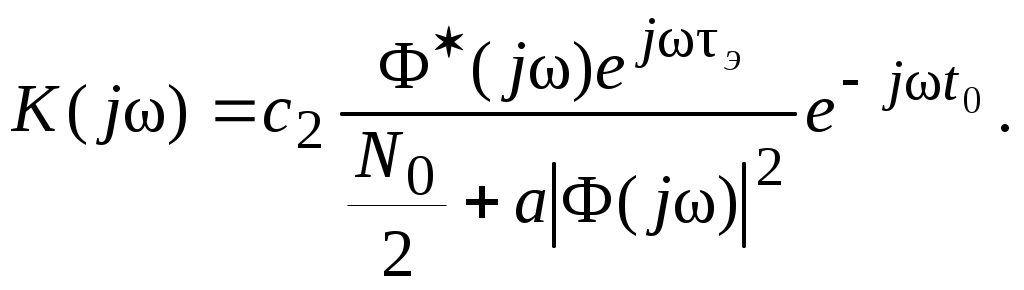
Пиковое отношение сигнал / помеха
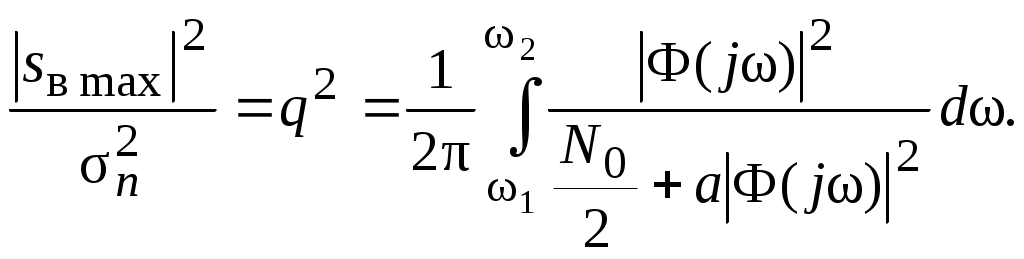 (1.22) (1.22)
Исследование последнего выражения показывает, что отношение сиг-нал / помеха максимально, когда амплитудный спектр сигнала 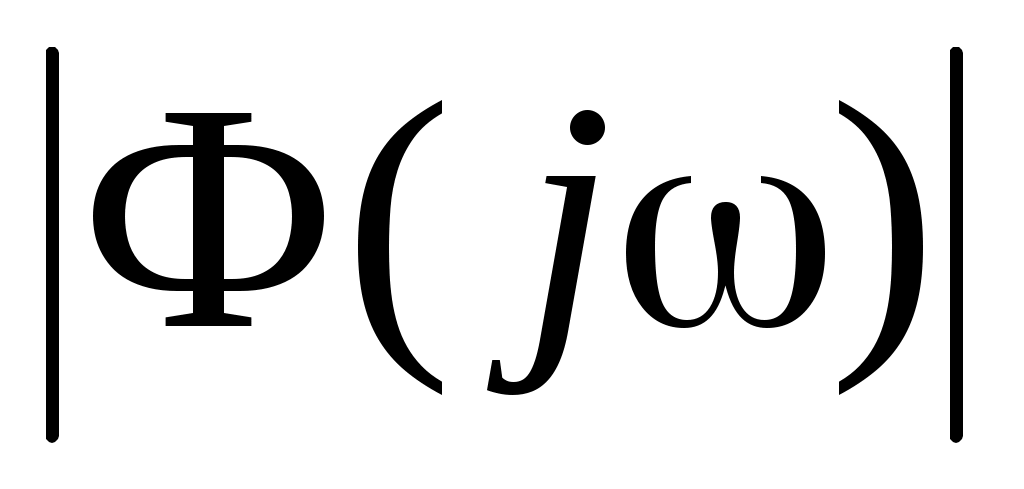 постоянен в заданной полосе частот, т. е. постоянен в заданной полосе частот, т. е.

Здесь Es – энергиязондирующего сигнала.
Подставляя это условие в формулу (2.22), получим

Таким образом, для минимизации влияния реверберационной помехи нужно использовать широкополосные сигналы с равномерным спектром. При этом увеличение ширины спектра сигнала при неизменной излучаемой мощности приводит к уменьшению значений спектральной плотности.
1.8. Оптимальная фильтрация сигналов по критерию минимума
среднеквадратической ошибки (сглаживающие и прогнозирующие
фильтры)
При классификации сигналов или измерении их параметров необходимо получить возможно более точную информацию об интересующем объекте. Иногда необходимо по обработанной части сигнала предсказать (достроить) значение сигнала в последующие моменты времени. Первую задачу – выделение сигнала из шумов с минимальными искажениями – решают так называемые сглаживающие фильтры, вторую задачу – прогнозирующие фильтры.
Для количественной оценки качества фильтрации можно использовать различные критерии. Наиболее употребительным является критерий минимизации среднего значения квадрата ошибки передачи сигнала
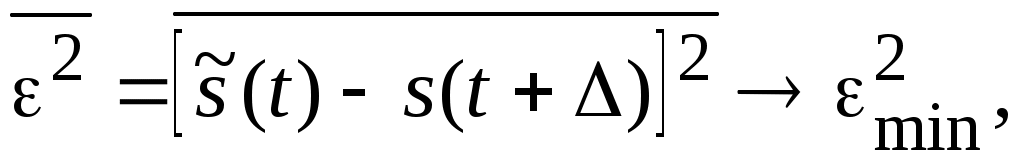
где s( t+ ) – значение сигнала в момент времени t+ ; – интервал времени прогнозирования сигнала;  – оценка сигнала в момент времени t , т. е. выходной сигнал фильтра в момент времени t . При D > 0 оценка – оценка сигнала в момент времени t , т. е. выходной сигнал фильтра в момент времени t . При D > 0 оценка  должна предсказывать значение входного сигнала s(t) на интервал D вперед. Ошибка e2 может быть определена, если известны корреляционные функции входного сигнала и шума. должна предсказывать значение входного сигнала s(t) на интервал D вперед. Ошибка e2 может быть определена, если известны корреляционные функции входного сигнала и шума.
Пусть на вход линейного фильтра поступает аддитивная смесь сигнала s(t) и помехи n(t): x(t) = s(t) + n(t). Требуется определить характеристики фильтра, выходной сигнал которого минимально отличался бы от истинного значения s(t+). Если = 0, то имеем дело со сглаживающим фильтром; если 0 и n(t) = 0, то фильтр прогнозирующий; если 0и n(t) 0, то у нас смешанный сглаживающе-прогнозирующий фильтр.
Р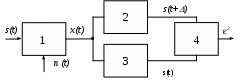
ассмотрим последний, наиболее общий случай, в предположении, что сигнал и помеха стационарны в широком смысле, время наблюдения tn = и известна вся предыстория процесса на интервале (-, t ).
|
 Скачать 1.91 Mb.
Скачать 1.91 Mb. (1.21)
(1.21)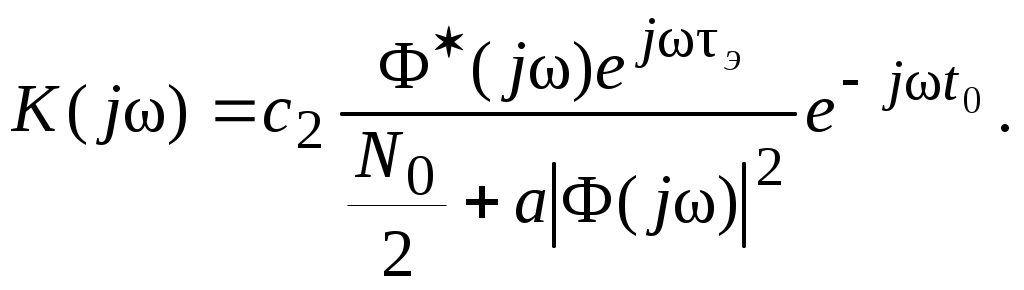
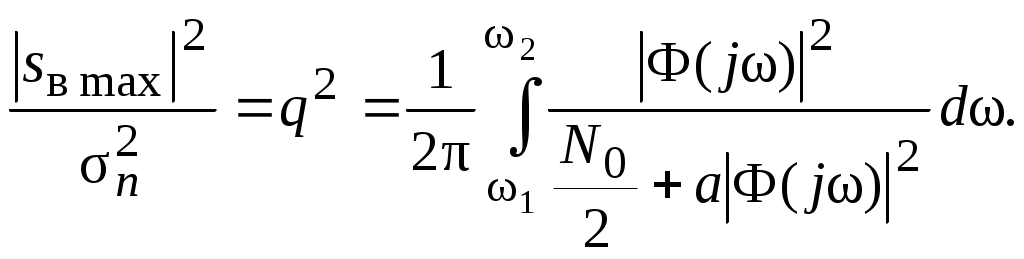 (1.22)
(1.22)

