МАИОС. МАОС без 1 главы (офворд 2003). 1. фильтрация сигналов на фоне помех
 Скачать 1.91 Mb.
|
Рис. 1.7Формальная структурная схема, поясняющая выбор критерия оптимальности фильтра, представлена на рис. 1.7. Здесь 1 – сумматор; 2 – идеальный фильтр; 3 – реальный фильтр; 4 – устройство вычисления ошибки. Пусть h(t) – импульсная характеристика реального фильтра. Тогда  ,и среднеквадратическая ошибка 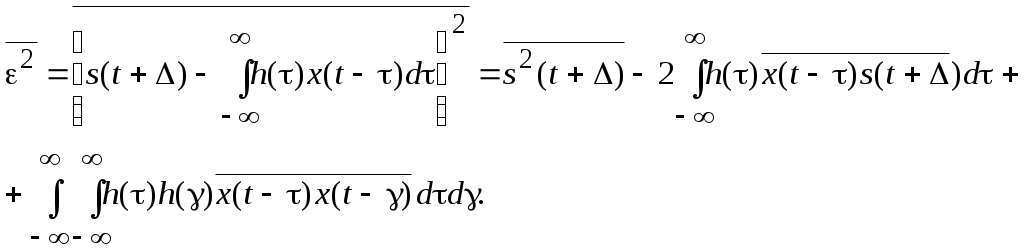 Для стационарных сигнала и помехи  – максимальное значение ковариационной функции сигнала;  – взаимная ковариационная функция принятой реализации и сигнала;  – ковариационная функция принятой реализации.Если hopt(t) – импульснаяхарактеристика оптимального фильтра, то среднеквадратическая ошибка для любого другого фильтра с импульсной характеристикой, которая представлена в виде h(t) = hopt(t)+g(t), (1.23) может быть только больше или равна среднеквадратической ошибке оптимального фильтра. Для фильтра, имеющего характеристику, описываемую формулой (1.23), среднеквадратическая ошибка с учетом сделанных ранее обозначений  Где 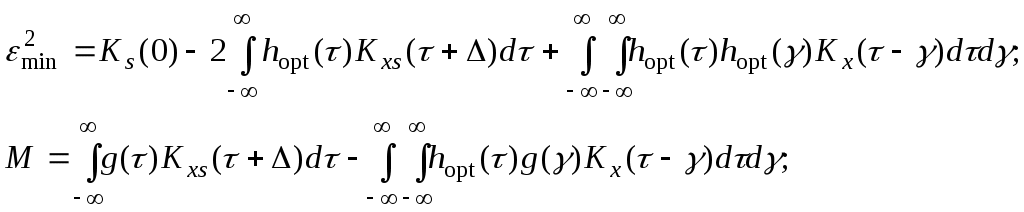  Минимум 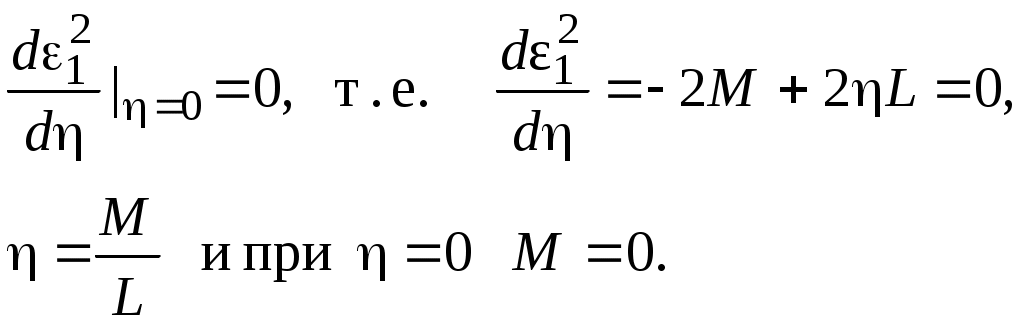 может быть найден из условия (1.24)Подробно расписывая условие (1.24), получим  Для любых g(t) это выражение справедливо лишь при  . (1.25)Отсюда видно, что импульсная характеристика оптимального фильтра может быть получена при решении интегрального уравнения (1.25). Это решение может быть получено с помощью теоремы о Фурье-преобразовании свертки. Действительно, так как интеграл в правой части есть свертка 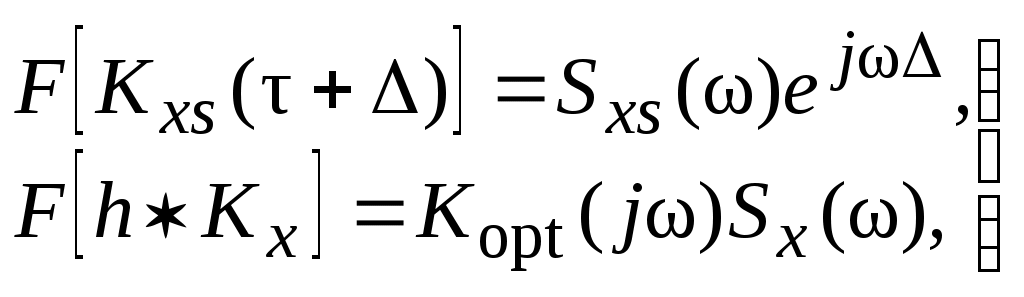 , то, взяв преобразование Фурье от левой и правой частей этого уравнения, получим (1.26)где F – обозначение преобразования Фурье, Sxs(w) – взаимная спектральная плотность принятого сообщения и сигнала; Sx(w) – спектральная плотность принятого сообщения; Kopt(j) – оптимальная частотная характеристика фильтра. Тогда уравнение (1.25) с учетом формул (1.26) запишется в виде  При независимых сигнале и помехе  С учетом этих соотношений получаем Это решение, строго говоря, описывает физически невозможный фильтр. Однако оно имеет практический смысл, так как приближенно применимо в тех случаях и с тем большей точностью, когда можно допустить большую задержку отклика фильтра относительно входного воздействия. Поэтому говорят, что это решение пригодно для фильтров с бесконечной задержкой. Для физически возможных фильтров импульсная характеристика h(t) в силу принципа причинности существует только для t>0 , так как сигнал на выходе фильтра не может появиться раньше начала импульса на входе. Для физически возможных фильтров уравнение (1.25) приводится к виду  т. е. к виду интегрального уравнения Винера-Хопфа, и должно решаться соответствующими методами. |