МАИОС. МАОС без 1 главы (офворд 2003). 1. фильтрация сигналов на фоне помех

• Название: 1. фильтрация сигналов на фоне помех
• Анкор: МАИОС
• Дата: 27.02.2022
• Размер: 1.91 Mb.
• Имя файла: МАОС без 1 главы (офворд 2003).doc
• Тип: Документы; #375573
• страница: 3 из 19

1.4. Согласованный фильтр и корреляционный приемник

Пусть на вход согласованного фильтра воздействует принятое колебание x(t)= s(t,₀) + n(t). Тогда сигнал на выходе согласованного фильтра можно представить в виде

. (1.12)

Интеграл в этом выражении носит наименование корреляционного интеграла. Действительно, с точностью до постоянного множителя он представляет собой взаимную ковариационную функцию принятого колебания x(t) и копии полезного сигнала s(t,l).

Выражение (1.12) можно записать также в виде

,

где

(1.13а)

– сигнальная функция;

(1.13б)

– шумовая функция.

Из соотношений (1.12) и (1.13а) следует, что полезный сигнал s_в(t) на выходе согласованного фильтра с точностью до постоянного размерного множителя k равен ковариационной функции входного полезного сигнала

,

взятой от аргумента t –-t₀ :

s_в(t) = kK(t – t₀),  s_{в max}(t₀) = kE_s. (1.14)

Следует также помнить, что в большинстве случаев фильтрации подвергаются высокочастотные сигналы (радиосигналы), у которых среднее значение равно нулю, и в этом случае ковариационная функция совпадает с корреляционной:

K(t) = R(t).

Таким образом, согласованный фильтр в принципе выполняет ту же операцию, что и корреляционный приемник; в этом смысле они эквивалентны. Вопрос о применении корреляционного приемника или согласованного фильтра в каждом конкретном случае решается в зависимости от простоты технической реализации. Следует отметить, что при одном и том же входном сигнале s(t,) характер сигнальной и шумовой функций на выходе корреляционного приемника и согласованного фильтра различен. Отличие в вычислении корреляционного интеграла корреляционным приемником и согласованным фильтром заключается в том, что коррелятор определяет единственную точку ковариационной функции сигнала, а именно максимальную точку, а согласованный фильтр вычисляет ковариационную функцию сигнала полностью.

Дисперсия шума на выходе согласованного фильтра может быть определена через выходной шум, равный на основании (1.12) и (1.13б):

n_в(t) q_0n(t).

Тогда корреляционная функция шума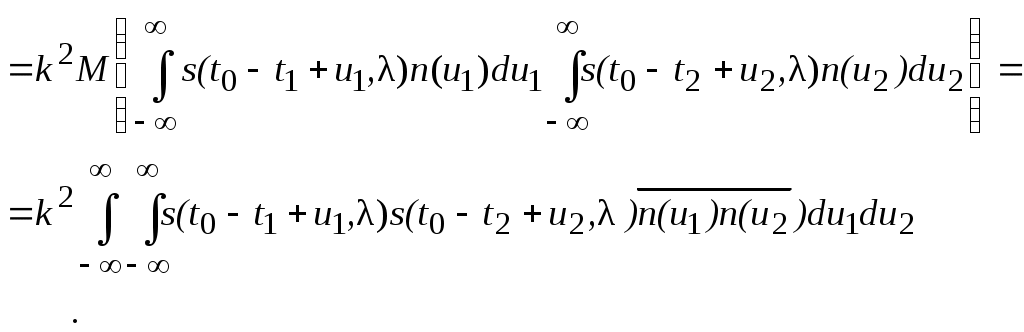





Но есть корреляционная функция белого шума:

.

Тогда в силу фильтрующего свойства d-функции интеграл отличен от нуля лишь при u₁ = u₂ = u и двойной интеграл переходит в однократный:

,

или, вводя замену t₀ –t₁ +u= t,

. (1.15)

Из формулы (1.15) видно, что корреляционная функция выходного шума имеет вид корреляционной функции входного сигнала. Тогда дисперсия выходного шума

D_в= . (1.16)

Из формул (1.14) и (1.16) находим отношение наибольшего значения выходного сигнала к среднеквадратическому значению выходного шума:

, (1.17)

где q – отношение сигнал/помеха по амплитуде.