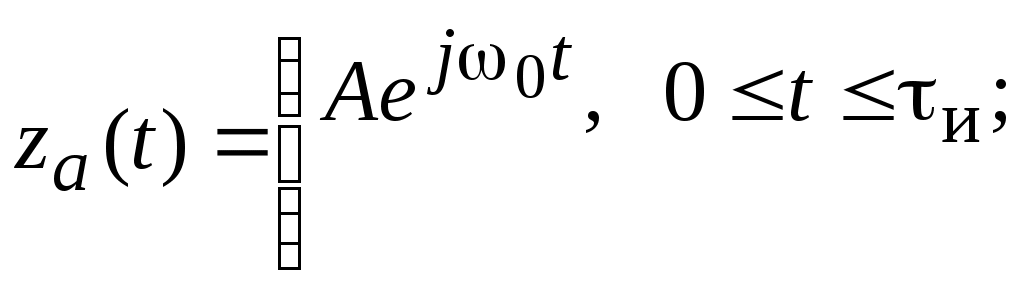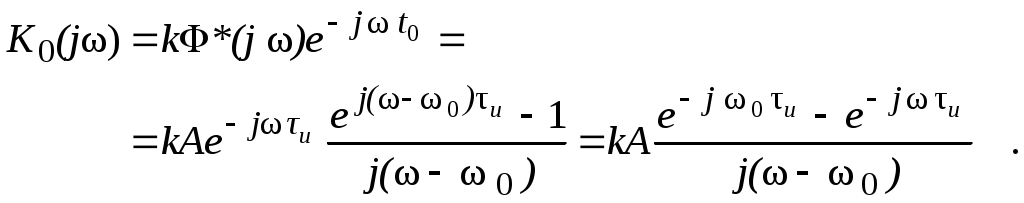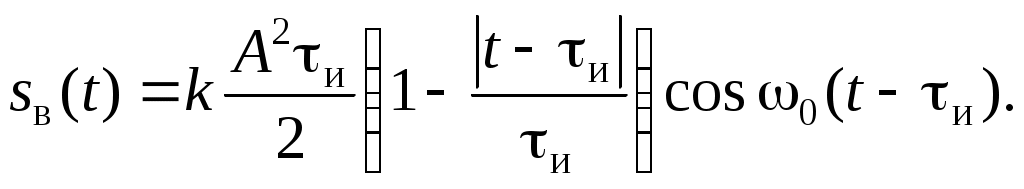Рассмотрим различные способы синтеза оптимальных фильтров. Фильтры для выделения сигнала на фоне коррелированного шума строятся обычно на основе спектрального метода, т. е. при использовании для комплексной частотной характеристики фильтра выражения (1.8).
Для согласованных фильтров, выделяющих сигнал на фоне белого шума, возможны два метода – спектральный и временной. Временной метод основан на использовании связи между импульсной характеристикой фильтра и сигналом согласно формуле (1.11). При этом синтез согласованного фильтра заключается в построении такого линейного устройства, импульсная характеристика которого с точностью до масштабного множителя и с некоторым запаздыванием воспроизводит функцию, являющуюся зеркальным отражением сигнала. Метод особенно удобен для сигналов симметричной формы, так как в этом случае зеркальное отражение сигнала совпадает с самим сигналом. По определению импульсная характеристика есть отклик линейной системы на d-функцию. Поэтому нужно так подбирать блоки согласованного фильтра, чтобы при действии на его входе -функции на выходе воспроизводился сигнал заданной формы и длительности.
1.6.1. Синтез согласованного фильтра для прямоугольного
видеоимпульса
Рассмотрим временной и спектральный методы синтеза фильтра на примере прямоугольного видеоимпульса:

Последовательность действий при синтезе временным методом иллюстрируется рис. 1.2.
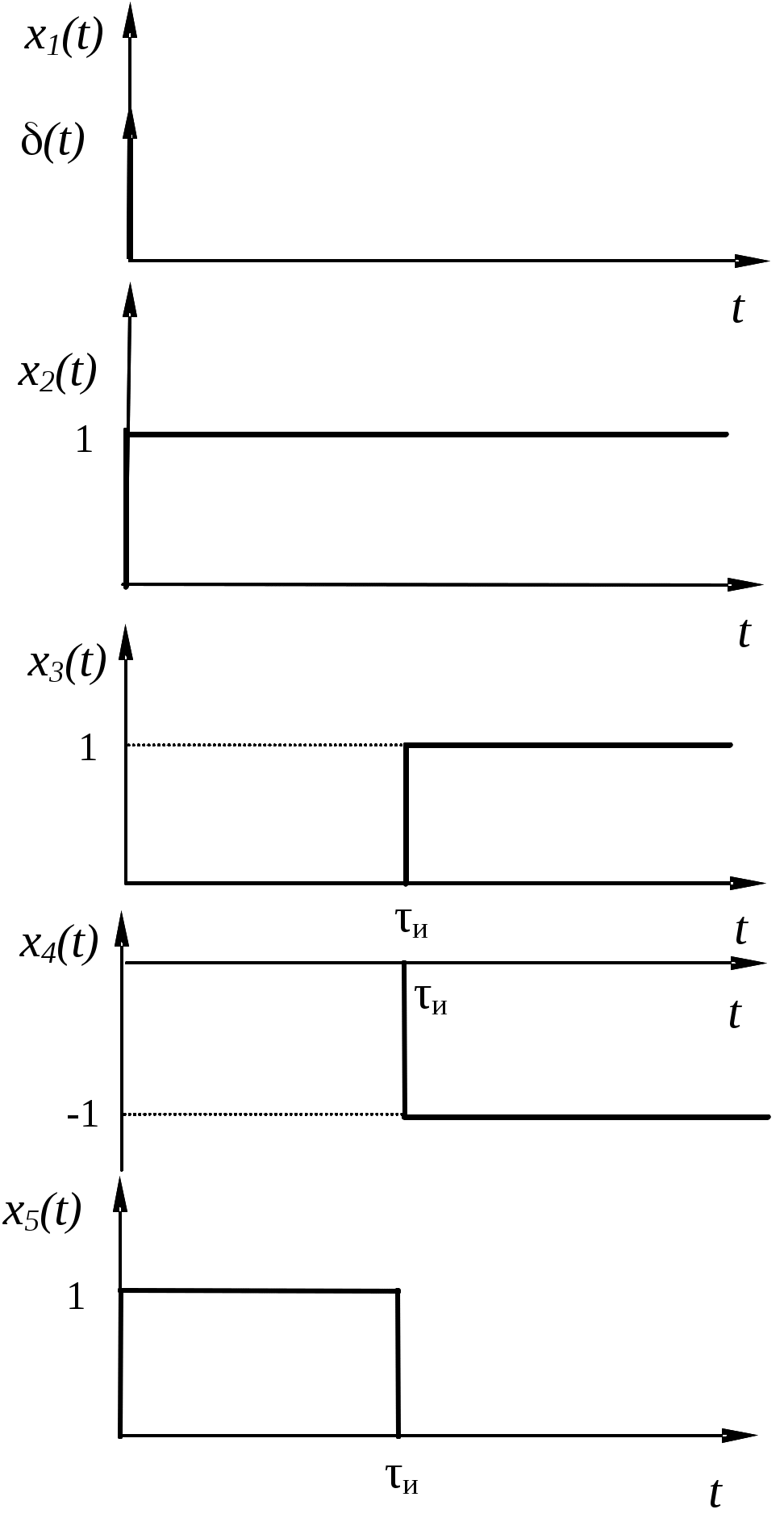
Рис. 2.2
Известно, что единичная ступенька (перепад), или функция Хевисайда Y(t), (x2(t)) есть интеграл от d-функции (x1(t)):

После задержки единичной ступеньки на длительность импульса tи (x3(t)), ее инвертирования (x4(t)) и вычитания из x2(t) получим заданный прямоугольный импульс x5(t), амплитуду которого можно изменять, меняя коэффициент передачи устройства. Отсюда следует, что искомый фильтр (рис. 1.3, а) состоит из интегратора 1, линии задержки на tи 2, инвертора 3, сумматора 4 и усилителя 5. Инвертор и сумматор могут быть заменены вычитающим устройством 6 (рис. 1.3, б). Работа обоих вариантов фильтра идентична.
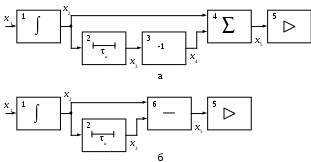
Рис. 1.3
Рассмотрим синтез фильтра спектральным методом. Комплексный спектр прямоугольного видеоимпульса
 . .
Для согласованного фильтра
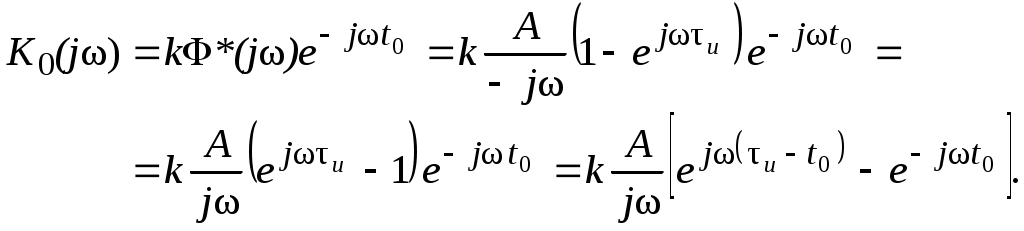
Полагая tи = t0 , окончательно получим
 (1.18) (1.18)
Рассмотрим члены, входящие в выражение (1.18). Оператор  , как известно, представляет собой оператор идеального интегрирования гармонического сигнала; kA – коэффициент передачи линейного устройства; , как известно, представляет собой оператор идеального интегрирования гармонического сигнала; kA – коэффициент передачи линейного устройства;  – задержку на время и. Видно, что структурная схема такого фильтра соответствует рис. 1.3. – задержку на время и. Видно, что структурная схема такого фильтра соответствует рис. 1.3.
Механизм работы согласованного фильтра (см. рис. 1.3) можно выяснить, рассматривая прохождение через него импульса сигнала и шума (рис. 1.4).
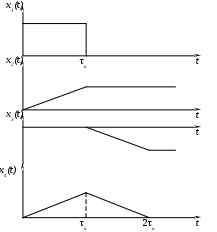
Рис. 1.4
Входной сигнал x1(t)с помощью интегрирующего устройства накапливается в течение времени и = t0 до своего пикового значения (x2 на рис. 1.4). Задержка на и(x3) и вычитание прекращают накопление сигнала, который уже дал на выходе максимальное значение, но вместе с тем прекращают и накопление шума. Выходной сигнал (x4) становится треугольным.
К аналогичному результату можно прийти, найдя аналитическое выражение для выходного полезного сигнала.
Для прямоугольного видеоимпульса ковариационная функция
 , ,
или, в силу симметрии ковариационной функции:  . .
Заменяя в последнем выражении t на t – t0 и полагая tи = t0 , на основании формулы (1.14) получаем
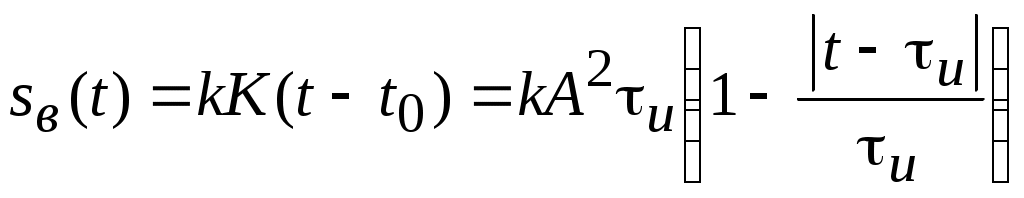 . .
График этой функции совпадает с приведенным на рис. 1.4. Видно, что длительность полезного сигнала на выходе фильтра удваивается.
Пусть шум на входе фильтра имеет спектральную плотность Sn(), отличную от равномерной:
 , ,
где 2a – спектральная плотность шума при w = 0; g–- постоянная, характеризующая ширину энергетического спектра.
В соответствии с выражением (1.8) тогда можно получить формулу для комплексной частотной характеристики оптимального фильтра для приема прямоугольного видеоимпульса на фоне коррелированного шума:
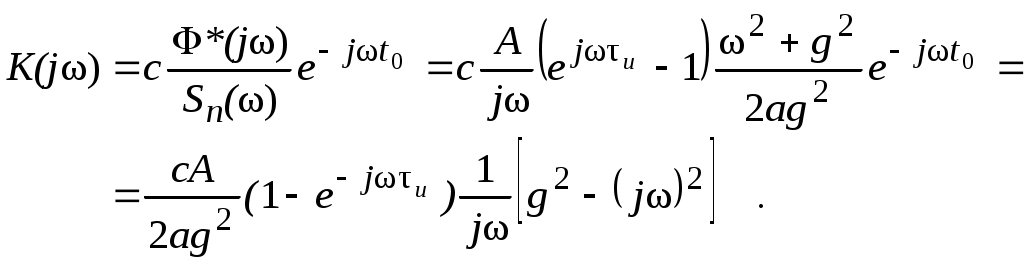 (1.19) (1.19)
Оператор jwсоответствует оператору идеального дифференцирования. Структурная схема оптимального фильтра, построенного в соответствии с формулой (1.19), изображена на рис. 1.5:

Рис. 1.5
На рисунке 6,7 – устройства дифференцирования; 8 – вычитатель. Назначение остальных блоков ясно из предыдущего.
Выражение (1.19) может быть преобразовано к виду
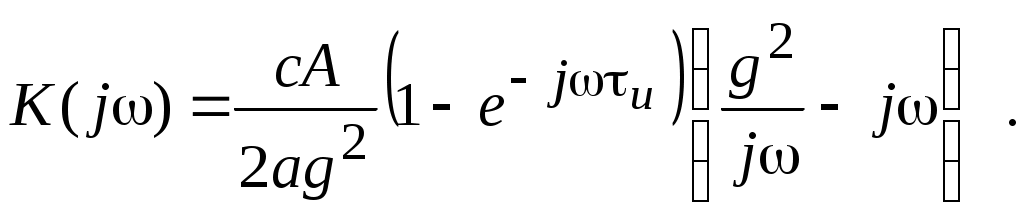
Структурная схема фильтра, соответствующая этому выражению, содержит на один блок меньше. Временной метод синтеза оптимальных фильтров для приема сигналов на фоне коррелированного шума используется редко, так как в этом случае передаточная функция фильтра обычно не позволяет построить структурную схему столь же просто, как это было сделано ранее.
1.6.3. Синтез фильтров, согласованных с радиоимпульсом
Очень часто на вход приемного устройства (например, ультразвукового эхоскопа) поступают радиоимпульсы, и оптимальные фильтры целесообразно реализовывать для них. Пусть имеется радиоимпульс с прямоугольной огибающей
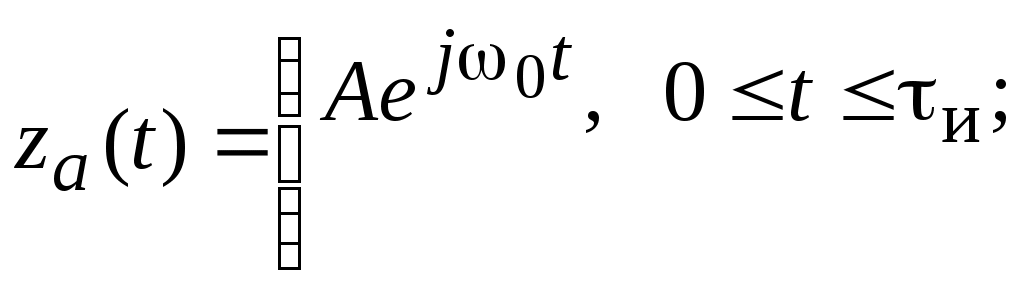
0 вне интервала .
Его комплексный спектр

Тогда комплексная частотная характеристика согласованного фильтра при t0= tи:
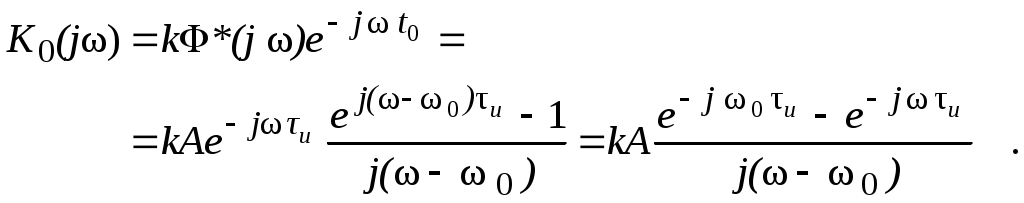
Если w0tи = 2np , где n–- целое число, т. е. импульс содержит целое число периодов, то  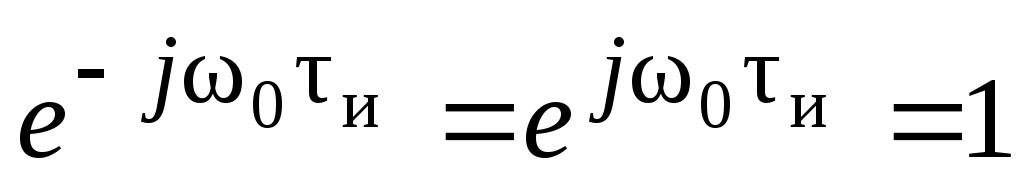 и и
  (1.20) (1.20)
Множитель j соответствует передаточной функции высокодобротного колебательного контура (при сопротивлении потерь, равном нулю). Сравнивая выражения (1.18) и (1.20), можно заметить, что при переходе от приема прямоугольного видеоимпульса к приему радиоимпульса с прямоугольной огибающей необходимо идеальный интегратор заменить на высокодобротный колебательный контур. Структурная схема согласованного фильтра для радиоимпульса с прямоугольной огибающей и формы входного и выходного сигналов показаны на рис. 1.6. Из него видно, что согласованный фильтр для радиоимпульса искажает входной сигнал, затягивает его, причем форма огибающей совпадает с формой сигнала на выходе фильтра, согласованного с прямоугольным видеоимпульсом.
Найдем выражение для выходного сигнала такого согласованного фильтра. При этом для упрощения вычислений используем соотношение [7]:
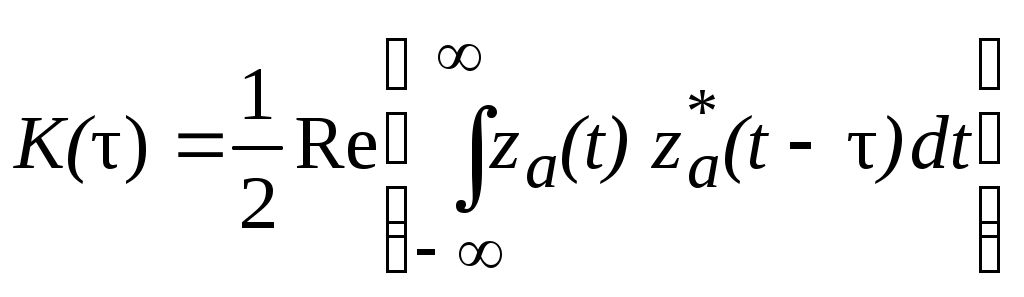 , ,
где za(t) – аналитический сигнал; Re - реальная часть. Подставляя сюда значение za(t), приведенное выше, получим:

или, в силу симметрии ковариационной функции,
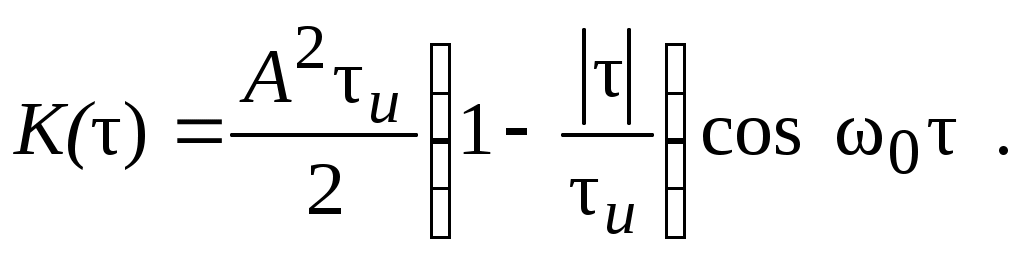
Тогда в соответствии с формулой (2.14) выходной сигнал имеет вид
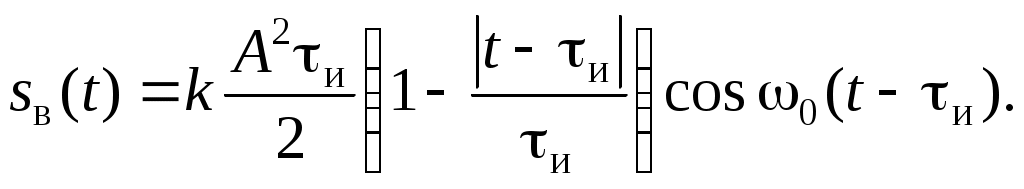
В
идно, что длительность треугольного радиоимпульса на выходе согласованного фильтра в два раза превышает длительность прямоугольного радиоимпульса на входе.
Рис. 1.6
На практике для фильтрации радиоимпульсов применяются квазиоптимальные фильтры в виде колебательных контуров с затуханием, систем таких контуров или активных полосовых фильтров. Возможно также использование различного рода электромеханических фильтров.
|
 Скачать 1.91 Mb.
Скачать 1.91 Mb.



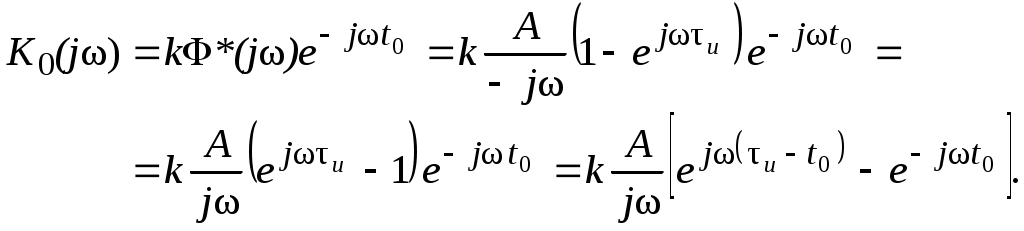

 ,
,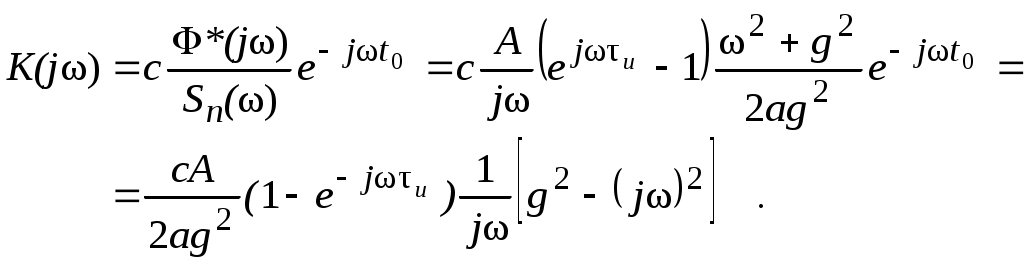 (1.19)
(1.19)