МАИОС. МАОС без 1 главы (офворд 2003). 1. фильтрация сигналов на фоне помех

• Название: 1. фильтрация сигналов на фоне помех
• Анкор: МАИОС
• Дата: 27.02.2022
• Размер: 1.91 Mb.
• Имя файла: МАОС без 1 главы (офворд 2003).doc
• Тип: Документы; #375573
• страница: 11 из 19

2.6. Бинарное обнаружение полностью известного сигнала

Рассмотренный случай соответствует обнаружению очень короткого сигнала. При обнаружении сигналов конечной длительности, если не требуется очень высокое быстродействие, целесообразно строить обнаружитель так, чтобы использовать полную энергию сигнала. Пусть на вход обнаружителя воздействует смесь сигнала и помехи, описываемая формулой (2.1), где s(t,) – полностью известный сигнал длительностью T и верхней частотой спектра , а n(t) – квазибелый гауссовский шум с постоянной спектральной плотностью S_n()= N₀ /2в полосе частот . Тогда входное колебание x(t) можно разложить в ряд Котельникова

,



где

.

Тогда непрерывная функция x(t) сводится к многомерной случайной величине x = (x₁, x₂,...),которой можно сопоставить многомерную плотность распределения вероятностей p(x₁, x₂,..., x_n). Корреляционная функция квазибелого шума может быть записана в виде

,

дисперсия шума 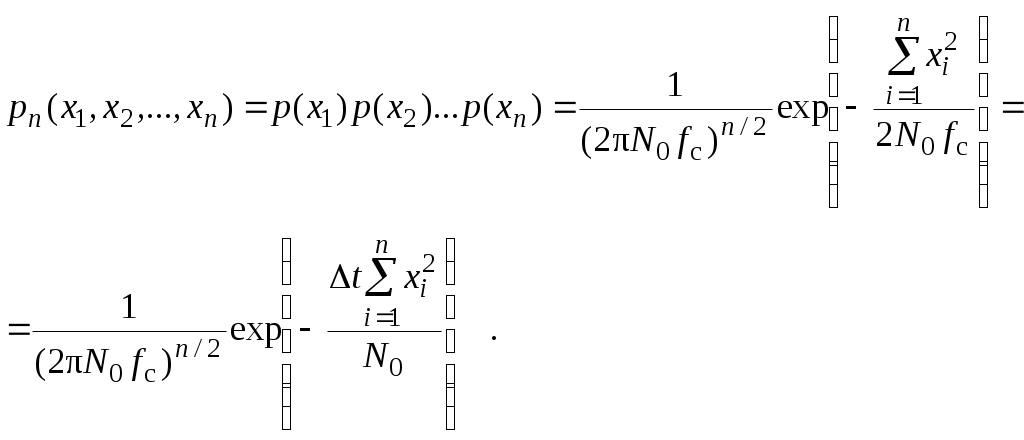. Известно также, что сечения квазибелого гауссовского шума, отстоящие на 1/2f_c , можно считать независимыми. Тогда многомерная плотность вероятностей может быть определена как произведение независимых плотностей вероятностей сечений x_i:

_(2.12)

Аналогично, плотность распределения вероятностей смеси сигнала с шумом запишется в виде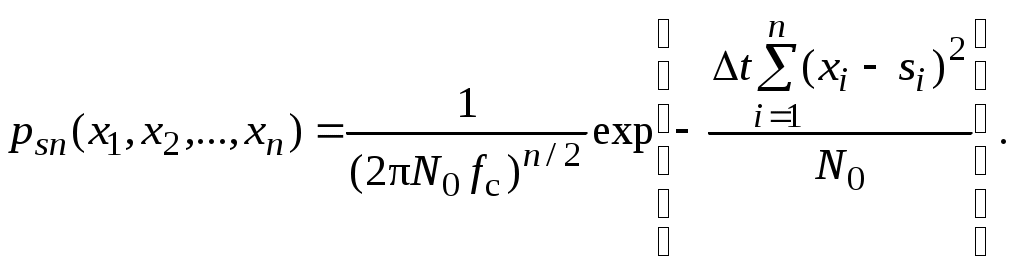

(2.13)

где s₁ , s₂,...,s_i ,...,s_n– значения полезного сигнала, взятые в сечениях.

С учетом формул (2.12) и (2.13) можно записать отношение правдоподобия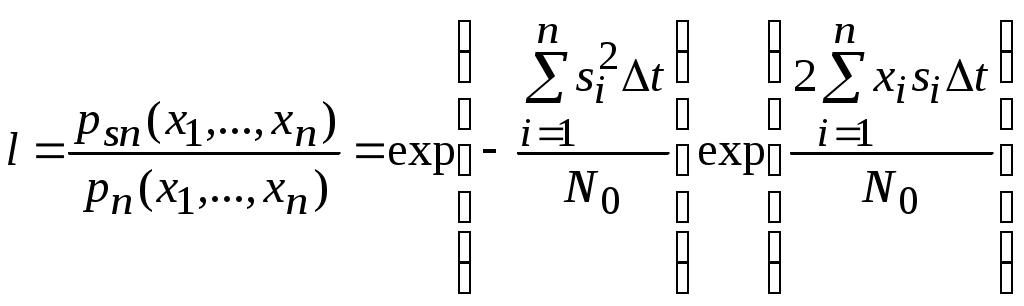

.

Переходя от квазибелого шума к белому при T = const, f_c®  , Dt® 0 , получим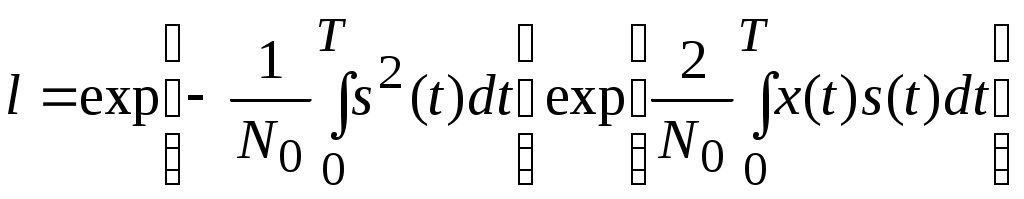

,

где – энергия сигнала; – корреляционный интеграл.

С учетом этих обозначений отношение правдоподобия для полностью известного сигнала имеет вид

(2.14)

Видно, что отношение правдоподобия является монотонной функцией корреляционного интеграла. В этом случае можно перейти от сравнения с порогом l₀отношения правдоподобия l(x) к сравнению с порогом z₀ значений корреляционного интеграла: z > z₀ – сигнал есть; z < z₀ – сигнала нет.

С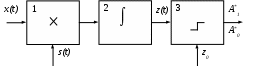
труктурная схема оптимального обнаружителя представлена на рис. 2.5, где 1 – перемножитель, 2 – интегратор, 3 – пороговое устройство.
Рис. 2.5
Обнаружитель вычисляет корреляционный интеграл и сравнивает его с порогом. При z > z₀принимается решение о наличии сигнала, при z < z₀ – решение об его отсутствии.

Перемножитель и интегратор преобразуют многомерное распределение на входе обнаружителя в одномерное распределение на выходе интегратора. Поскольку операция вычисления корреляционного интеграла является линейной, при гауссовском законе распределения на входе обнаружителя значения корреляционного интеграла также будут иметь гауссовское распределение [9] . При нулевом среднем на выходе перемножителя (т. е. в тех случаях, когда полезный сигнал отсутствует) среднее значение выходного сигнала интегратора также будет равно нулю. Тогда дисперсия выходного сигнала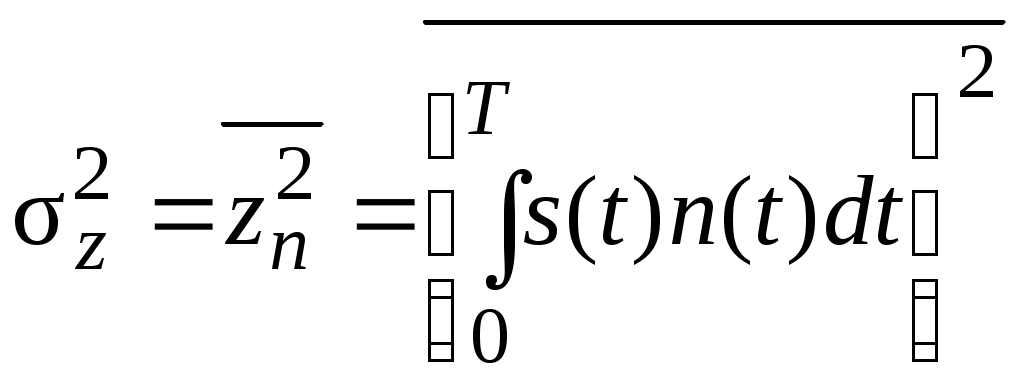

.

Заменив квадрат интеграла произведением двух интегралов и изменив порядок интегрирования и усреднения, получим:



В подынтегральном выражении есть ко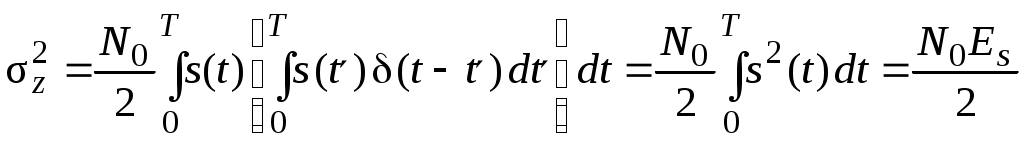рреляционная функция шума. Для белого шума



Отсюда

.

В присутствии сигнала на входе обнаружителя на выходе интегратора будем иметь

.

Первый интеграл равен энергии сигнала, а второй – корреляционный интеграл при наличии на входе только шума. Очевидно, что тогда величина z_sn распределена по гауссовскому закону со средним, равным энергии сигнала E_s, и дисперсией 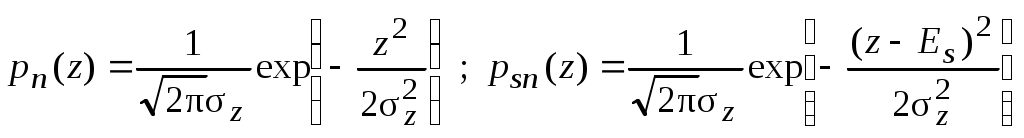. Тогда можно записать выражения для плотностей распределения на выходе интегратора при отсутствии (p_n(z)) и наличии (p_sn(z)) сигнала на входе:

. (2.15)

Отсюда аналогично формулам (2.8) и (2.10) можно получить выражения для условных вероятностей ложной тревоги и правильного обнаружения:

, (2.16)

и
ли аналогично (2.11) при работе по критерию Неймана-Пирсона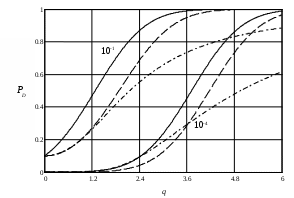

(2.16 а)

где   – относительный порог регистрации; – отношение сигнал/помеха. Рассчитанные по выражениям (2.16) кривые обнаружения полностью известного сигнала (сплошные линии) при различных вероятностях ложной тревоги (10^-1 и 10^-4) приведены на рис. 2.6.



Рис. 2.6
Другим часто используемым представлением для свойств обнаружителя являются рабочие или оперативные характеристики (рис. 2.7). Оперативные характеристики показывают зависимость условной вероятности правильного обнаружения от условной вероятности ложной тревоги в соответствии с выражением (2.16 а). При этом значение отношения сигнал / помеха играет роль параметра семейства кривых. Из анализа этих характеристик следует:

1) при условной вероятности ложной тревоги P_F = 0 условная вероятность правильного обнаружения P_D = 0независимо от значения отношения сигнал / помеха;

2) чем больше отношение сигнал / помеха при заданной условной вероятности ложной тревоги P_F , тем больше условная вероятность правильного обнаружения P_D ;

3) условная вероятность правильного обнаружения P_D может быть точно равна 1 лишь при P_F = 1.

Таким образом становится очевидной невозможность построения идеального обнаружителя, решающего задачу обнаружения без наличия ошибок первого и второго рода. Эти ошибки неизбежны, и следует лишь стремиться к возможному их уменьшению. В особо ответственных ситуациях необходимо либо использовать дублирование систем обнаружения сигналов, например применяя несколько обнаружителей, работающих на разных физических принципах, либо применять более сложные алгоритмы решения задачи обнаружения.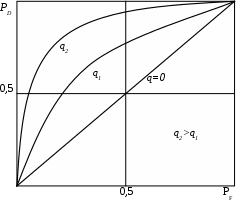





Рис. 2.7
Описанная в подразделе 1.4 пропорциональность выходного сигнала коррелятора и согласованного фильтра позволяет применять последний в оптимальных обнаружителях. Структурная схема подобного обнаружителя детерминированного сигнала изображена на рис. 2.8. На вход согласованного фильтра 1 подается смесь x(t) полезного сигнала и белого или квазибелого шума. Сигнал с выхода согласованного фильтра y(t), который в соответствии с выражением (1.12) с точностью до произвольной постоянной равен значению корреляционного интеграла:

,

в пороговом устройстве 2 сравнивается с пороговым значением y₀= kz₀. При превышении максимальным значением этого уровня (y_max(t)> y₀) принимается решение о наличии полезного сигнала, в противном случае (y_max(t)< y₀ ) – о его отсутствии. Если спектр частот детерминированного сигнала занимает полосу более узкую, чем спектр помехи, то при построении характеристик фильтра можно пренебречь ограниченностью спектра помехи и считать шум белым, т. е. для фильтрации можно применять согласованный фильтр. Закон распределения помехи и смеси сигнал / помеха на выходе фильтра останется гауссовским (узкополосное устройство «нормализует», т. е. приближает закон распределения к гауссовскому даже для процессов, отличных от гауссовского). Однако параметры законов распределения на выходе фильтра будут отличаться от параметров на его входе и могут быть определены по заданной комплексной частотной характеристике фильтра.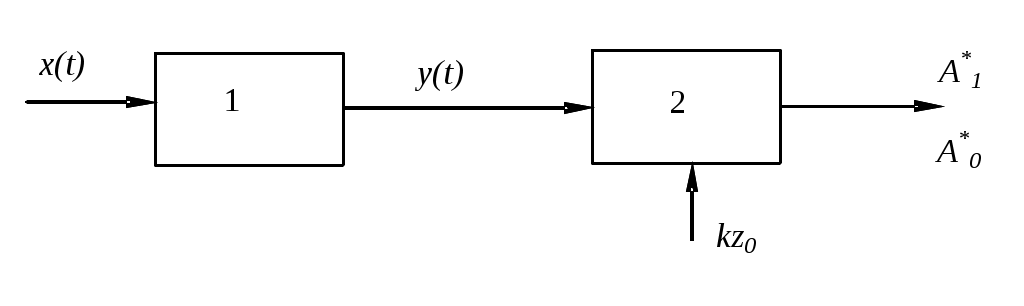



Рис. 2.8
Характеристики обнаружения для приемника на рис. 3.8 могут быть рассчитаны по формулам (2.15) – (2.16), но с учетом того, что в соответствии с выражением (1.16) дисперсия шума на выходе оптимального фильтра



На практике порог часто устанавливают по дисперсии шума на выходе приемника. Тогда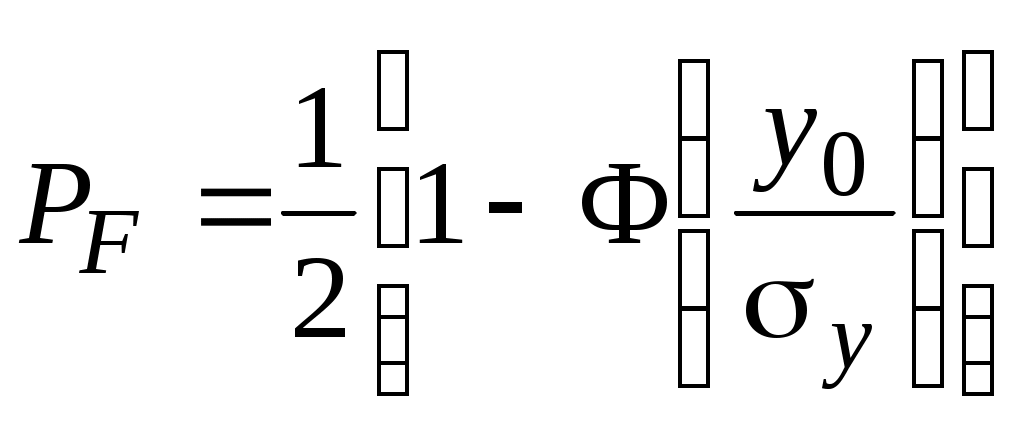

.

Необходимо отметить, что в реальных условиях детерминированные сигналы, как правило, не встречаются. Поэтому приведенные результаты следует рассматривать как теоретический верхний предел для характеристик обнаружения. Этот предел не может быть превышен в практических ситуациях, и можно лишь стремиться к его достижению.