МАИОС. МАОС без 1 главы (офворд 2003). 1. фильтрация сигналов на фоне помех

• Название: 1. фильтрация сигналов на фоне помех
• Анкор: МАИОС
• Дата: 27.02.2022
• Размер: 1.91 Mb.
• Имя файла: МАОС без 1 главы (офворд 2003).doc
• Тип: Документы; #375573
• страница: 18 из 19

3.4. Последовательный обнаружитель

Рассмотренные ранее обнаружители пачек сигналов предполагают использование фиксированного времени наблюдения (время интегрирования T_и для обнаружителя с поcледетекторным интегрированием или максимальное количество импульсов k₀ для обнаружителя с двоичным накоплением). Однако в некоторых случаях соотношение амплитуд сигнала и помехи позволяет надежно обнаруживать сигнал быстрее, чем в других циклах наблюдения. Поэтому, если заранее не фиксировать общую длительность наблюдения, можно за много циклов наблюдения получить значительную экономию времени. Такой метод анализа, названный последовательным, был предложен Вальдом [5]. При последовательном обнаружении производятся непрерывный анализ отношения правдоподобия (или монотонно связанной с ним величины) и сравнение его с двумя порогами l₁ и l₂:

, причем l₂ > l₁.

Если выполняется условие l < l₁, то принимается решение о наличии только помехи. Если выполняется условие l > l₂ , то принимается решение о наличии полезного сигнала. И, наконец, если значение отношения правдоподобия лежит между порогами: l₁ < l < l₂ , то делается вывод, что имеющихся данных недостаточно для обоснованного заключения о наличии или отсутствии сигнала, и принимается решение «не знаю». При этом испытание продолжается до тех пор, пока не прекратятся ответы «не знаю».

Преимущество последовательного обнаружителя состоит в том, что можно независимо задавать вероятности P_Fи P_D. Кроме того, он дает определенную экономию во времени принятия решения или в энергии излучаемого сигнала. Выигрыш по чувствительности (по значению отношения сигнал/помеха, необходимого для получения той же помехоустойчивости при том же среднем времени обнаружения) составляет от 3 до 20 дБ. Однако применение последовательного анализа требует значительного усложнения аппаратуры.

В настоящее время разработаны некоторые варианты последовательного анализа, упрощающие его реализацию. Например, в двухэтапном обнаружителе с первым порогом сравнивается результат накопления M импульсов. Если порог не превышен ни в одном элементе, то излучается еще N импульсов, производится сравнение со вторым порогом и выдается более уверенное решение (т. е. с меньшей вероятностью ложной тревоги) о наличии или отсутствии сигнала. Выигрыш по сравнению с однопороговой системой зависит от отношения сигнал/помеха, значений M и N и составляет не менее 2...3 дБ.

3.5. Обнаружение коррелированных сигналов

В ряде случаев помехи бывают связаны с неинформативными параметрами исследуемого объекта. Примерами таких помех являются реверберация в море и в металле, отражения от структурных неоднородностей тканей человеческого тела (кровеносные сосуды и т. п.). При ультразвуковом контроле это, например, помехи, связанные с шероховатостью и загрязнениями поверхности контролируемых изделий, и т. д. В результате увеличение длительности контроля одной и той же точки изделия, например посылка нескольких импульсов при одном и том же положении датчика, не приводит к повышению отношения сигнал/помеха, так как помеха, как и значение полезного сигнала, жестко связаны с положением датчика относительно изделия. В этом случае накопление эффективно при движении датчика относительно объекта, если полезный сигнал может быть зарегистрирован не в одной точке, а на протяжении некоторого отрезка линии сканирования, и помеха при таком перемещении датчика флуктуирует. Тогда совокупность сигналов на выходе приемного датчика при его движении можно рассматривать как реализацию случайного процесса x(t). (При импульсном характере работы рассматривается огибающая амплитуд принимаемых импульсов.)

Рассмотрим пересечение стационарного дифференцируемого процесса x(t) с постоянным уровнем C . Согласно [6], среднее число выбросов этого процесса за уровень C :

,

где  ; – двухмерная плотность вероятностей ординаты случайного процесса x(t) и его производной; L – длина реализации. Интенсивность выбросов, т. е. количество выбросов на единицу длительности,



Для дальнейшего решения задачи необходимо задаться видом двухмерной плотности, т. е. видом закона распределения сигнала x(t). Рассмотрим случай ультразвукового теневого контроля стальных горячекатаных изделий. Как показывают эксперименты [12], [13], в этом случае закон распределения огибающей амплитуд U(t) можно считать гауссовским. Учитывая, что при теневом контроле на бездефектном участке среднее значение амплитуд должно быть выше порога, можно получить, что интенсивность ложной тревоги (перебраковки), т. е. среднее количество выбросов – ложных регистраций дефектов на единицу длины пути сканирования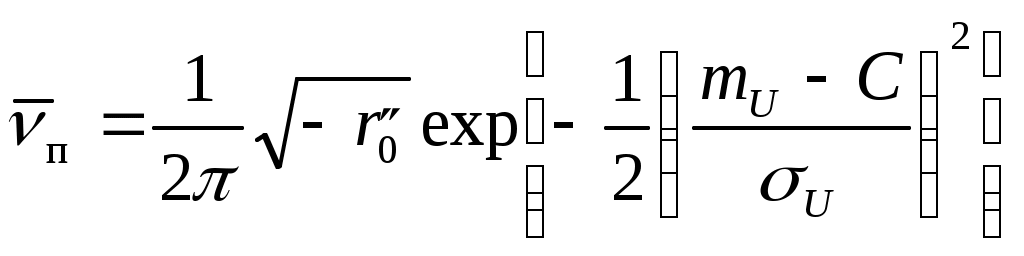

.

Если в изделии имеется протяженный дефект с акустической прозрачностью T , то на дефектном участке интенсивность пропуска цели (недобраковки), т. е. среднее количество пропусков в регистрации дефектов,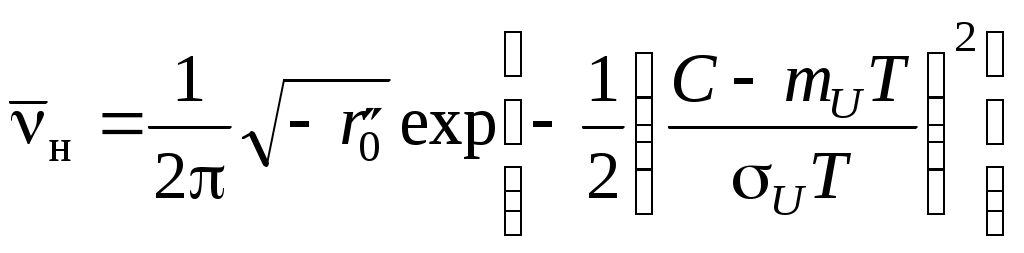

.

Здесь m_U – среднее значение огибающей амплитуд на бездефектном участке контролируемого изделия; – дисперсия огибающей амплитуд; – значение второй производной нормированной корреляционной функции огибающей амплитуд в точке t = 0.

Вводя в двух последних выражениях нормировку по уровню среднего значения, получим:

; (3.7)

. (3.8)
Здесь – коэффициент вариации огибающей амплитуд. Формулы (3.7) и (3.8) позволяют получить выражения для относительного порога регистрации u:
, (3.9)

. (3.10)

Приравнивая правые части выражений (3.9) и (3.10), можно записать выражение для максимальной акустической прозрачности T_max протяженного дефекта, который выявляется с заданной надежностью (заданными ):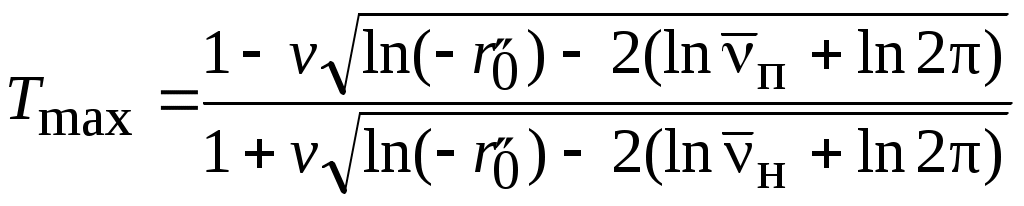

.

Взаимное расположение огибающей амплитуд и порогового уровня на бездефектном и дефектном участках показаны на  рис. 3.4.





Рис. 3.4
Проведенное рассмотрение справедливо для случая, когда необходимо учитывать лишь одномерные корреляционные связи огибающих амплитуд сигналов. Однако при контроле изделия по всей его площади при бесконечно малом шаге сканирования совокупность результатов контроля можно рассматривать как реализацию случайного поля амплитуд, что требует учета двухмерных корреляционных связей. Соответствующее рассмотрение на основе теории выбросов случайных полей проведено в [14] без учета и с учетом конечности значения шага сканирования в продольном и поперечном направлениях. Приведенные там же результаты расчетов показали, что в большинстве случаев для реальных параметров сканирования можно пренебречь корреляционными связями сигналов в одном направлении и рассчитывать чувствительность и надежность контроля по приведенным ранее формулам.
3.6. Достоверность результатов обнаружения
Как было показано, для расчета максимальной чувствительности обнаружения необходимо задаться интенсивностями ложной тревоги и пропуска цели. При выполнении условия выбросы гауссовского стационарного процесса можно считать независимыми. Аналогично, будут независимыми выбросы за достаточно высокий уровень (т. е. уровень, далеко отстоящий от среднего значения) и для других законов распределения сигнала. В ряде случаев указанное условие может быть даже ослаблено. Так, можно показать, что уровень, выше которого выбросы являются практически независимыми, обусловлен видом нормированной корреляционной функции процесса. Например, для гауссовского процесса при выбросы независимы уже при Но если появление отдельных выбросов можно считать независимыми редкими событиями, то их число на определенной длине реализации подчиняется закону Пуассона. Тогда доверительная вероятность того, что число выбросов, т. е. ложных регистраций сигнала, на длине реализации L не превысит n₀,

, (3.11)

где – среднее число выбросов на длине реализации L . Таким образом, задавшись доверительной вероятностью P получения не более n₀ложных регистраций сигнала на длине реализации L, можно определить среднее число регистраций , и средняя интенсивность ложных регистраций .

Аналогично можно записать выражение для доверительной вероятности P_д того, что в записи сигнала длиною L_д будет не более n_д пропусков:

, (3.12)

где – среднее значение количества пропусков в записи сигнала длиною L_д . Отсюда определяется средняя интенсивность пропусков (недобраковки): . Величины P, n₀ , P_д , n_д должны выбираться, исходя из необходимости обеспечения заданной надежности обнаружения и возможного снижения уровня ложной тревоги.

Точно так же могут быть определены вероятности ложной тревоги и пропуска цели и в случае, когда не требуется учета корреляционных связей сигналов в соседних точках. В этом случае задается доверительная вероятность P появления не более n₀ ложных регистраций сигнала в N₀ точках анализа. Среднее число ложных регистраций при этом определится из условия (3.11), а вероятность ложной тревоги в каждой точке контроля . Если минимальный подлежащий учету объект должен занимать не менее M_д элементов разрешения (M_д ³ 1) и задана доверительная вероятность P_D получения не более n_д пропусков регистрации такого объекта, то среднее число пропусков определится из формулы (3.12) и вероятность пропуска цели в каждой из точек наблюдения . Полученные значения P_F и могут быть использованы для определения значений порогов регистрации в рассмотренных схемах обнаружителей.