Физика 9 класс. 1. Физика. Методы познания природы. Физические явления
 Скачать 5.42 Mb. Скачать 5.42 Mb.
|
11. Механическая энергия и ее виды. Закон сохранения энергии.Механическая энергия бывает двух видов: кинетическая и потенциальная. Кинетическая энергия (или энергия движения) определяется массами и скоростями рассматриваемых тел. Потенциальная энергия (или энергия положения) зависит от взаимного расположения (от конфигурации) взаимодействующих друг с другом тел. Работа определяется как скалярное произведение векторов силы и перемещения. Скалярным произведением двух векторов называется скаляр равный произведению модулей этих векторов и косинус угла между ними. Понятия энергии и работы тесно связаны друг с другом. Кинетическая энергия частицы (4) Приняв во внимание, что произведение mV равно модулю импульса частицы р, выражению (4) можно придать вид Если сила F , действующая на частицу, не равна нулю, кинетическая энергия получит за время dt приращение (5) где ds - перемещение частицы за время dt. Величина называется работой, совершаемой силой F на пути ds (ds - модуль перемещения ds). Из (5) следует, что работа характеризует изменение кинетической энергии, обусловленное действием силы на движущуюся частицу Если dA = Fds, а Проинтегрируем обе части равенства (6) вдоль траектории частицы от точки 1 до точки 2: 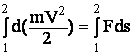 . .Левая часть полученного равенства представляет собой приращение кинетической энергии частицы: Правая часть есть работа А12 силы F на пути 1-2: Таким образом, мы пришли к соотношению , (7) из которого следует, что работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы. Консервативные силы Силы, работа которых не зависит от пути, по которому двигалась частица, а зависит лишь от начального и конечного положений частицы, называются консервативными. Легко показать, что работа сил на любом замкнутом пути равна нулю. Разобьем произвольный замкнутый путь (рис.1) точками 1 и 2 (взятыми также произвольно) на два участка, обозначенных римскими цифрами I и II. Работа на замкнутом пути слагается из работ, совершаемых на этих участках:
Рис.1 Изменение направления движения по участку II на обратное сопровождается заменой всех элементарных перемещений ds на -ds, вследствие чего изменяет знак на обратный. Отсюда заключаем, что . Произведя замену в (8), получим, что Вследствие независимости работы от пути последнее выражение равно нулю. Таким образом, консервативные силы можно определить как силы, работа которых на любом замкнутом пути равна нулю. Потенциальная энергия Эта энергия определяется положением тела (высотой на которое оно поднято). Поэтому она называется энергией положения. Чаще ее называют потенциальной энергией. Ep = mgh, где h отсчитывается от произвольного уровня. В отличие от кинетической энергии, которая всегда положительна, потенциальная энергия может быть как положительной, так и отрицательной. Пусть частица движется в поле консервативных сил. При переходе из точки 1 в точку 2 над ней совершается работа A12 = Ep1-Ep2 . (9) В соответствии с формулой (7) эта работа равна приращению кинетической энергии частицы. Приняв оба выражения для работы, получим соотношение , из которого следует, что . (10) Величина E, равная сумме кинетической и потенциальной энергий, называется полной механической энергией частицы. Формула (10) означает, что E1=E2, т.е. что полная энергия частицы, движущейся в поле консервативных сил. Остается постоянной. Это утверждение выражает закон сохранения механической энергии для системы, состоящей из одной частицы. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ Рассмотрим систему, состоящую из N взаимодействующих друг с другом частиц, находящихся под воздействием внешних как консервативных, так и неконсервативных сил. Силы взаимодействия между частицами предполагаются консервативными. Определим работу, совершаемую над частицами при перемещении системы из одного места в другое, сопровождающимся изменением конфигурации системы. Работа внешних консервативных сил может быть представлена как убыль потенциальной энергии системы во внешнем силовом поле: где определяется формулой (9). Работа внутренних сил равна убыли взаимной потенциальной энергии частиц: , где - потенциальная энергия системы во внешнем поле сил. Работу неконсервативных сил обозначим . Согласно формуле (7) суммарная работа всех сил затрачивается на приращение кинетической энергии системы Ek, которая равна сумме кинетических энергий частиц: 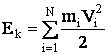 Следовательно, Сгруппируем члены этого соотношения следующим образом: Сумма кинетической и потенциальной энергий представляет собой полную механическую энергию системы E: . Таким образом, мы установили, что работа неконсервативных сил равна приращению полной энергии системы: (11) Из (11) следует, что в случае, когда неконсервативные силы отсутствуют, полная механическая энергия системы остается постоянной: Мы пришли к закону сохранения механической энергии, который гласит, что полная механическая энергия системы материальных точек, находящихся под действием только консервативных сил, остается постоянной. Если система замкнута и силы взаимодействия между частицами консервативны, то полная энергия содержит только два слагаемых: ( - взаимная потенциальная энергия частиц). В этом случае закон сохранения механической энергии заключается в утверждении, что полная механическая энергия замкнутой системы материальных точек, между которыми действуют только консервативные силы, остается постоянной. |

