Физика 9 класс. 1. Физика. Методы познания природы. Физические явления
 Скачать 5.42 Mb. Скачать 5.42 Mb.
|
50. Тепловое действие электрического тока. Закон Джоуля-Ленца.Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения по нему тока. Теперь этот закон называют законом Джоуля — Ленца. Математически он выражается в виде следующей формулы: Q=I2×R×t. Нагревание током проводника обусловлено взаимодействием носителей тока со встречными атомами или ионами вещества. В результате этого взаимодействия внутренняя энергия проводника возрастает и он нагревается. Нагретый проводник отдает полученную энергию окружающей среде. Эта энергия и представляет собой то количество теплоты, которое определяется по закону Джоуля — Ленца. Закон Джоуля — Ленца был открыт экспериментально. Но ему можно дать и теоретическое обоснование. Когда электрический ток проходит по проводнику, совершается работа, определяемая выражением A=IUt. Но U=IR. Поэтому A=I2×R×t. Если проводник, по которому идет ток, остается неподвижным и в нем не происходит никаких химических реакций, то вся эта работа идет на увеличение его внутренней энергии. При этом количество теплоты, выделяемое проводником с током, совпадает с работой тока и поэтому определяется тем же выражением. При очень большом токе металлический проводник может раскалиться и перегореть (расплавиться). На этом основано действие плавких предохранителей. Их назначение — автоматическое отключение электрической цепи, когда в ней начинает идти ток больше допустимого.. Тепловое действие тока. Закон Джоуля — Ленца 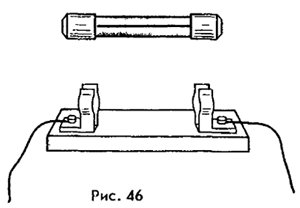 На рисунке 46 изображен предохранитель, используемый в радиоэлектронной аппаратуре. Его главной частью является проволочка из легкоплавкого металла (например, свинца), толщина которой рассчитана на определенный ток (0,5 А, 1 А, 2 А и т.д.). Если сила тока по той или иной причине (например, при коротком замыкании) превысит допустимое значение, проволочка расплавится и цепь окажется разомкнутой. Электрическая проводка в жилых зданиях рассчитана, как правило, на 6 А или 10 А. Используемые для ее защиты квартирные предохранители (пробки) показаны на рисунке 47, а, б. В первом случае (см. рис. 47, а) после перегорания нити заменяют всю пробку, во втором случае (см. рис. 47, б) лишь ее плавкую вставку. 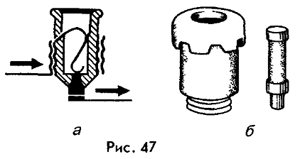 51.Электрический ток в металлах.Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику переноса вещества не происходит, следовательно, ионы металла не принимают участия в переносе электрического заряда. Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов. Идея таких опытов и первые качественные результаты (1913 г.) принадлежат русским физикам Л. И. Мандельштаму и Н. Д. Папалекси. В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюарт усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением электронов. Схема опыта Толмена и Стюарта показана на рис. 1.12.1. Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру Г. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра. 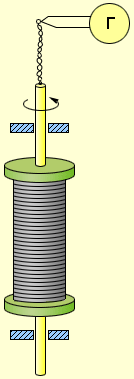 При торможении вращающейся катушки на каждый носитель заряда e действует тормозящая сила которая играет роль сторонней силы, то есть силы неэлектрического происхождения. Сторонняя сила, отнесенная к единице заряда, по определению является напряженностью Eст поля сторонних сил: Следовательно, в цепи при торможении катушки возникает электродвижущая сила , равная где l – длина проволоки катушки. За время торможения катушки по цепи протечет заряд q, равный Здесь I – мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ0 – начальная линейная скорость проволоки. Отсюда удельный заряд e / m свободных носителей тока в металлах равен: Все величины, входящие в правую часть этого соотношения, можно измерить. На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона, полученному из других опытов. Так было установлено, что носителями свободных зарядов в металлах являются электроны. По современным данным модуль заряда электрона (элементарный заряд) равен
а его удельный заряд есть
Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема. Предположение о том, что за электрический ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 году немецкий ученый П. Друде на основании гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории. Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла (рис. 1.12.2). 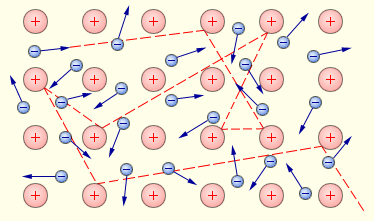 Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер. Высота этого барьера называется работой выхода. При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера. Из-за взаимодействия с кристаллической решеткой потенциальная энергия выхода электрона внутри проводника оказывается меньше, чем при удалении электрона из проводника. Электроны в проводнике находятся в своеобразной «потенциальной яме», глубина которой и называется потенциальным барьером. Как ионы, образующие решетку, так и электроны участвуют в тепловом движении. Ионы совершают тепловые колебания вблизи положений равновесия – узлов кристаллической решетки. Свободные электроны движутся хаотично и при своем движении сталкиваются с ионами решетки. В результате таких столкновений устанавливается термодинамическое равновесие между электронным газом и решеткой. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость теплового движения электронов по формулам молекулярно-кинетической теории. При комнатной температуре она оказывается примерно равной 105 м/с. При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток. Среднюю скорость дрейфа можно оценить из следующих соображений. За интервал времени Δt через поперечное сечение S проводника пройдут все электроны, находившиеся в объеме Число таких электронов равно где n – средняя концентрация свободных электронов, примерно равная числу атомов в единице объема металлического проводника. Через сечение проводника за время Δt пройдет заряд Отсюда следует:
или
Концентрация n атомов в металлах находится в пределах 1028–1029 м–3. Оценка по этой формуле для металлического проводника сечением 1 мм2, по которому течет ток 10 А, дает для средней скорости упорядоченного движения электронов значение в пределах 0,6–6 мм/c. Таким образом, средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения Рис. 1.12.3 дает представление о характере движения свободного электрона в кристаллической решетке. 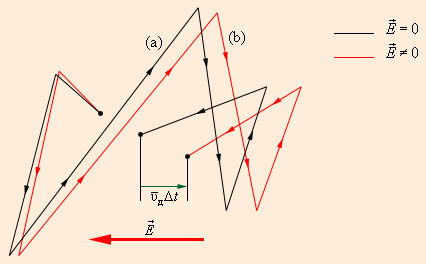 Малая скорость дрейфа на противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·108 м/с. Через время порядка l / c (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов. В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью. Несмотря на то, что все эти допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках. |
