Связь между напряженностью электрического поля и потенциалом. 11. Связь между напряженностью электрического поля и потенциалом
 Скачать 132.84 Kb.
|
|
11. Связь между напряженностью электрического поля и потенциалом  Связь между напряженностью электрического поля и потенциалом аналогична связи между потенциальной энергии и силой. Работа сил может быть представлена как убыль потенциальной энергии заряда, то есть как  А также как  приравнивая эти выражения, находим, что Где через l обозначено произвольно выбранное направление в пространстве. В частности, 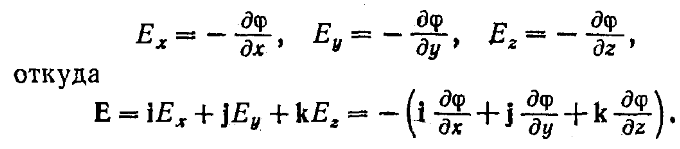 Выражение, стоящее в скобках, называется градиентом скаляра ჶ. Таким образом, напряженность электрического поля равна градиенту потенциала, взятому с обратным знаком. Градиент некоторой скалярной функции есть векторная величина, обладающая следующими свойствами: Направление градиента совпадает с направлением n, в котором при смещении из данной точки функция, возрастая по величине, изменяется с наибольшей скоростью. Величина производной dჶ/dn по этому направлению дает модуль градиента. Частные производные dჶ/dx, dჶ/dy, dჶ/dz представляют собой проекции градиента на координатные оси x,y,z. Проекция градиента на перпендикулярное к нему направление r равна нулю: dჶ/dr=0.  - разность потенциалов между двумя точками, взятыми в однородном поле напряженности E, причем под d следует понимать в этом случае проекцию расстояния l12 между точками 1 и 2 на направление вектора E.12. Эквипотенциальные поверхности  Эквипотенциальная поверхность – это такая поверхность, все точки которой имеют одинаковый потенциал. Если потенциал задан как функция x,y,z уравнение эквипотенциальной поверхности имеет вид Направление нормали к эквипотенциальной поверхности будет совпадать с направлением вектора Е в той же точке. Эквипотенциальную поверхность можно провести через любую точку поля. Проводить поверхности нужно так, чтобы разность потенциалов для двух соседних поверхностей была всюду одна и та же. Чем гуще располагаются эквипотенциальные поверхности, тем быстрее изменяется потенциал при перемещении вдоль нормали к поверхности. 13. Полярные и неполярные молекулы В составе атомов и молекул имеются положительно заряженные ядра и отрицательно заряженные электроны. Электроны движутся в пределах атома или молекулы с огромной скоростью, непрерывно изменяя свое положение относительно ядер. Для расстояний, больших молекулы, действие электронов эквивалентно действию их суммарного заряда, помещенного в некоторую точку внутри молекулы. Назовем эту точку центром тяжести отрицательных зарядов. Положение центра тяжести зарядов определяется как положение обычного центра тяжести, но с заменой масс частиц их зарядами. Радиус-вектор центра тяжести положительных зарядов вычисляется по формуле  Где r+i – радиус-вектор точки, в которой помещается i-й положительный заряд, q – суммарный положительный заряд молекулы. Аналогично для радиуса-вектора центра тяжести отрицательных зарядов:  Где r-j – радиус-вектор усредненного по времени положения j-го отрицательного заряда. В отсутствие внешнего электрического поля центры тяжести положительных и отрицательных зарядов могут совпадать или быть сдвинутыми друг относительного друга. В последнем случае молекула эквивалентна электрическому диполю и называется полярной. Она обладает собственным электрическим моментом p, для которого получается следующее:  Где qk – алгебраическая величина. Молекулы, у которой центры тяжести зарядов разных знаков в отсутствии поля совмещены, собственным электрическим моментом не обладает и называется неполярной. В рационализованной системе коэффициент пропорциональности записывают в виде ɛ0β, где ɛ0 электрическая постоянная, а β – величина, называемая поляризуемостью молекулы. Можно записать p= βe0Е. Полярная молекула ведет себя во внешнем поле как жесткий диполь. 14. Диполь в однородном и неоднородном электрических полях Если диполь поместить в однородное электрическое поле, образующие диполь заряды окажутся под действием равных по величине, но противоположных по направлению сил f1 и f2. Эти силы образуют пару, плечо которой равно lsinα, т.е. зависит от ориентации диполя относительно поля. Модуль каждой из сил равен qE. Момент пары сил, действующих на диполь равен  где p-электрический момент диполя. В векторном виде формула равна  Энергия диполя равна нулю в том случае, когда диполь устанавливается перпендикулярно к полю. Наименьшее значение энергии получается при ориентации диполя по направлению поля, наибольшее – при р, направленном в сторону, противоположную Е. В неоднородном поле силы, действующие на заряды диполя, неодинаковы по величине. При малых размерах диполя силы f1 и f2 можно приближенно считать коллинеарными. В неоднородном поле на диполь кроме вращательного момента действует сила  Под ее действием диполь будет втягиваться в область более сильного поля, либо вталкиваться из нее.24. Электроемкость Различные по величине заряды распределяются на удаленном от других тел проводнике подобным образом, то есть отношение плотностей проводника при любой величине заряда будет одно и то же. Потенциал уединенного проводника пропорционален находящемуся на нем заряду. Для уединенного проводника  Коэффициент пропорциональности C между потенциалом и зарядом называется электроемкостью проводника.  Емкость уединенного шара радиуса R, погруженного в однородный безграничный диэлектрик с относительной проницаемостью ɛ, равна  За единицу емкости принимают емкость такого проводника, потенциал которого изменяется на 1 в при сообщении ему зарядка в 1 к. Эта единица емкости называется фарадой(ф).  25. Конденсаторы В основу конденсаторов положено, что электроемкость проводника возрастает при приближении к нему других тел. При поднесении к заряженному проводнику какого-либо тела потенциал проводника уменьшается по абсолютной величине. Это означает увеличение емкости проводника. Конденсаторы бывают плоские, цилиндрические, сферические. Под емкостью конденсатора понимается физическая величина, пропорциональная заряду q и обратно пропорциональная разности потенциалов между обкладками:  Величина емкости определяется геометрией конденсатора, а также диэлектрическими свойствами среды, заполняющей пространство между обкладками. Емкость плоского конденсатора:  Где S – площадь обкладки, d – величина зазора между обкладками, ɛ - относительная диэлектрическая проницаемость вещества, заполняющего зазор. Емкость цилиндрического и сферического конденсаторов равна  В случае, когда d=R2-R1< Напряженность поля между обкладками сферического конденсатора равна  26. Соединение конденсаторов При параллельном соединении одна из обкладок каждого конденсатора имеет потенциал ф1, а другая ф2. Емкость батареи  При параллельном соединении конденсаторов емкости складываются. Предельное напряжение батареи равно наименьшему из значений Umax для конденсаторов, включенных в батарею. 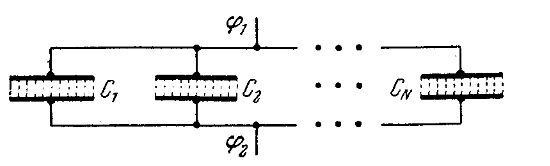 Последовательное соединение конденсаторов. Для всех конденсаторов, включенных последовательно, характерна одинаковая величина заряда q на обкладках. Поэтому напряжение на каждом из конденсаторов  Сумма этих напряжений равна разности потенциалов, приложенной к батарее, откуда получается, что  При последовательном соединении конденсаторов складываются величины, обратные их емкостям. 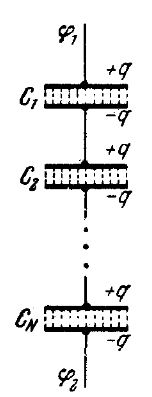 27. Энергия системы зарядов Силы, с которыми взаимодействуют заряженные тела, консервативны (их работа не зависит от пути). Система заряженных тел обладает потенциальной энергией.  где ф1 – потенциал, создаваемый зарядом q2 в той точке, в которую перемещается заряд q1. Работа переноса заряда q2 из бесконечности в точку, удаленную от q1 на r12, равна 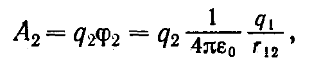 где ф2 – потенциал, создаваемый зарядом q1 в той точке, в которую перемещается заряд q2. Энергия системы значения работ:  В случае N зарядов потенциальная энергия системы равна  где фi – потенциал, создаваемый в той точке, где находится qi , всеми зарядами, кроме i-го. 28. Энергия заряженного проводника Заряд q, находящийся на некотором проводнике, можно рассматривать как систему точечных зарядов   где ф – потенциал проводника, обусловленный уже имеющимся на нем зарядом q, С – емкость проводника. Энергия напряженного проводника равна нулю. Тогда можно записать :  Поверхность проводника является эквипотенциальной, поэтому потенциалы трех точек, в которых находятся точечные заряды , одинаковы и равны потенциалу ф проводника. |