геомеханика. 1. Геомеханика как раздел горной науки, основные понятия и определения
 Скачать 136.16 Kb. Скачать 136.16 Kb.
|
|
5.1. Прочностные свойства горных пород Прочностные св-ва опред-т способность пород сопротивляться разрушению под действием приложенных механических напряжений. Они ха-ся пределами прочности при сжатии и растяжении, сцеплением и углом внутреннего трения. Пределом прочности 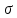 называется напряжение, при котором образец разрушается. называется напряжение, при котором образец разрушается. 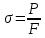 , F-площадь, Р-нагрузка. , F-площадь, Р-нагрузка.Предел прочности на одноосное сжатие образца наиболее широко опред-я ха-ка прочности гп ( 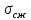 ) ) 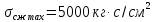 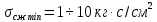 В зависимости от состава и структуры пород даже одного петрографического наименования, прочность на сжатие может колебаться в весьма больших пределах. Обычно прочность пород тем 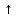 , чем , чем 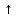 их плотность. их плотность.Прочность на растяжение ( 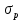 ) значительно ниже их прочности на сжатие. Это одна из наиболее характеризованных особенностей гп, определяет их поведение в поле механических сил. Действительно, для сталей ) значительно ниже их прочности на сжатие. Это одна из наиболее характеризованных особенностей гп, определяет их поведение в поле механических сил. Действительно, для сталей 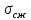 и и 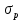 др материалов показатели и равны между собой. др материалов показатели и равны между собой.Гп плохо сопротивляются растягивающим усилиям, появление которых в тех или иных участках массива гп при разработке служит критериями опасности обрушения гп и разрушения горных выработок. Отношение 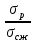 весьма показательно для сравнительной ха-ки различных пород. В механике гп его обычно выражают в виде простой дроби с единицей в числителе. Это отношение колеблется от весьма показательно для сравнительной ха-ки различных пород. В механике гп его обычно выражают в виде простой дроби с единицей в числителе. Это отношение колеблется от 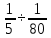 , среднее , среднее 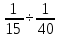 . . 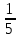 - ха-ет глинистую породу, - ха-ет глинистую породу,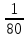 - наиболее хрупкие (гранит, песчаник и др). - наиболее хрупкие (гранит, песчаник и др).Прочность на срез (сдвиг) может быть ох-на двумя функционально связанными па-ми: сцеплением и углом внутр трения породы. Эту ф-ю связь выражают ур-ем Кулона 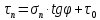 , , 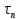 -напряжение среза; -напряжение среза;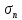 - норм напряжение при срезе; - норм напряжение при срезе;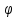 - угол внутр трения; - угол внутр трения;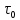 - сцепление. - сцепление.Сцепление 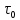 (К) ха-ет предельное сопротивление срезу по площадке, на которой отсутствует норм давление, те нет сопротивления срезающим усилиям за счет внутр трения. (К) ха-ет предельное сопротивление срезу по площадке, на которой отсутствует норм давление, те нет сопротивления срезающим усилиям за счет внутр трения.Угол внутр трения 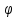 ( (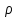 ) или коэф внутр трения ха-ет интенсивность роста срезающих напряжений с ) или коэф внутр трения ха-ет интенсивность роста срезающих напряжений с 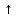 норм напряжений, те представляет собой коэф пропорциональности между приращениями касательных ( норм напряжений, те представляет собой коэф пропорциональности между приращениями касательных (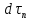 ) и нормальных ( ) и нормальных (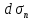 ) напряжений при срезе ) напряжений при срезе 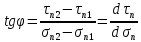 Значение сцеплении гп меняется а пределах 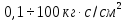 . .Угол внутреннего трения 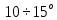 для некоторых глин и для прочных массивных кристаллических для некоторых глин и для прочных массивных кристаллических 5.2 Плотностные свойства горных пород Плотностные св-ва гп проявляются в результате действия гравитационного поля земли. Их делят на 2 группы: гравитационные и структурные. К гравитационным свойствам относят удельный 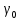 и объемный вес пород и объемный вес пород 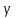 , удельную массу , удельную массу 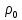 , плотность (объемную массу) , плотность (объемную массу) 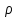 , к структурным — общую П и открытую пористость П0. , к структурным — общую П и открытую пористость П0.Удельный вес – вес единицы объема тв фазы породы 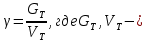 вес и объем ТВ фазы породы. Значение удельного веса гп в зависимости от удельного веса породообразующих минералов колеблется в пределах 2%-5гр/см3. вес и объем ТВ фазы породы. Значение удельного веса гп в зависимости от удельного веса породообразующих минералов колеблется в пределах 2%-5гр/см3.Объемный вес – это отношение веса основных агрегатных фаз породы к объему, занимаемому этими фазами 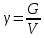 . . Объемный вес – наиболее часто используемая плотностная ха-ка, которая зависит от вида их состава и структуры. Он всегда меньше удельного веса. Удельная масса - 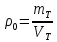 - отношение массы тв фазы гп к объему тв фазы гп. - отношение массы тв фазы гп к объему тв фазы гп.Плотность (объемная масса) гп опред-я как масса к единице ее объема 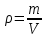 . .Удельная масса и плотность породы выражаются через 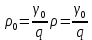 , где q – ускорение силы тяжести. , где q – ускорение силы тяжести.В отличие от удельного и объемного веса плотность явл параметром вещества в строго физическом смысле. Наибольшую плотность имеют массивно-кристаллические изверженные породы, наименьшую – осадочные и эффузивные (вулканические туфы, пемзы) Пористость – суммарный относительный объем содержащихся в породе пустот. Суммарный отн объем открытых пор ха-ет открытую пористость гп (По), а закрытых – закрытую (Пи). Пористость, которой опред-я движение в породе жидкостей и газов называют эффективной пористостью (Пэ). Общая пористость (П) опред-я совокупностью закрытых, открытых пор, поры разделяют по размеру на 3 класса: сверхкапиллярные (более 0,1 мм), капиллярные (от 0,0002 до 0,1 мм), субкапиллярные (менее 0,0002 мм). Пористость выражают в % 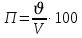 (отношение объема пор к полному объему породы). Пористость гп изменяется в широких приделах (от доли % до 90 и более). Принято различать породы с пористостью низкой (менее 5%), пониженной (5-10%), средней (10-15%), повышенной 15-20%, высокой (более 20%). (отношение объема пор к полному объему породы). Пористость гп изменяется в широких приделах (от доли % до 90 и более). Принято различать породы с пористостью низкой (менее 5%), пониженной (5-10%), средней (10-15%), повышенной 15-20%, высокой (более 20%).6. Упругие свойства горных пород Упругие св-ва гп ха-ся модулем упругости Е при одноосном напряженном состоянии – модулем предельной упругости (модулем Юнга). Модуль сдвига (G), модуль объемной упругости (К) и коэф поперечных деформаций ( 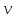 ) (коэф Пуассона) ) (коэф Пуассона)Модуль упругости Е представляет собой отношение норм напряжений к относительной линейной упругой деформации образца 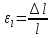 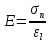 Модулем сдвига G является отношение касательных напряжений 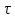 к относительному сдвигу к относительному сдвигу 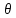 : : 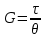 , где , где 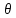 - относительный сдвиг или угловая деформ, он ха-ет изменение форм и деформ тела и выражается зависимостью: - относительный сдвиг или угловая деформ, он ха-ет изменение форм и деформ тела и выражается зависимостью: 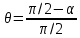 ; ; 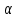 - угол наклона каждого прямоугольно элемента тела после деформ. - угол наклона каждого прямоугольно элемента тела после деформ.Объемный модуль упругости (К) или модуль всестороннего сжатия равен отношению равномерного, всестороннего напряжения к относительному упругому изменению объема образца: 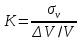 Коэф поперечных деформ 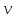 (коэф Пуассона)– мера пропорциональности между относительными деформациями в направлении (коэф Пуассона)– мера пропорциональности между относительными деформациями в направлении 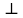 к вектору приложения нагрузки и к вектору приложения нагрузки и 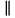 ему: ему: 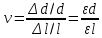 Перечисленные характеристикики упругих св-тв связаны между собой отношениями: 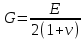 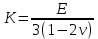 Таким образом зная 2 из этих ха-к, можно расчетным путем определить значение др. обычно экспериментальным путем опред на образцах пород хар-ки Е и 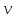 . Модули упругости колеблятся . Модули упругости колеблятся 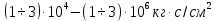 С ростом плотности пород модули их упругости возрастают. Модули упругости слоистых пород в направлении 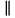 выше, чем выше, чем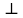 . .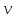 в ГП теоретически меняются в пределах от 0 до 0,5. Для многих пород колеблется от 0,15 до 0,35. в ГП теоретически меняются в пределах от 0 до 0,5. Для многих пород колеблется от 0,15 до 0,35.7. Акустические свойства горных пород Акустические сво-ва опред условия распространения в ГП упругих колебаний. Характеризуются скоростью распространения упругих волн, акустическим сопротивлением и коэффициентом поглощения ( 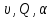 соотв) соотв)Среди различного вида колебаний в тв телах наибольший интерес представляют продольные, поверхностные и поперечные волны. В продольных волнах направление колебаний частиц совпадает с направлением распространения волны, в поперечных направлениях колебания частиц 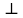 направлению распространения волны. направлению распространения волны.Поверхностные волны – колебаниями пов-ти среды (пов-ти образца ГП). Соотношение между скоростями продольных 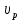 , поперечных , поперечных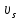 , и поверхностных упругих волн характеризуются неравенством: , и поверхностных упругих волн характеризуются неравенством: 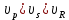 Скорости распространения упругих волн опред скоростью характеризующей смещаемую массу и показателей упругости среды, связывающими возвращающие силы со смещением колеблющихся частиц. Теоретические взаимосвязи этих скоростей деформ ха-ми и плотностью среды имеют следующие выражения: 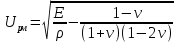 ; 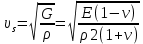 ; ; 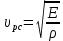 ; ; 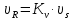 ; ; 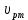 -скорость продольной волны в неограниченной среде; -скорость продольной волны в неограниченной среде;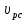 -скорость продольной волны в стержне; -скорость продольной волны в стержне;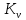 - безразмерный коэф, зависящий от коэф поперечных деформ. - безразмерный коэф, зависящий от коэф поперечных деформ.(при 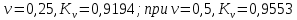 ) )Произведение плотности породы на скорость соотв волны называют акустическим сопротивлением (акустической плотностью): 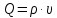 Оно ха-ет влияние св-тв среды на интенсивность, частоту, колебаний в этой среде. Так как ГП не явл идеально упругими тв телами, в них происходят колебания, возбуждаемые упругими волнами, вследствие поглощения энергии колебаний в среде из-за трения, теплопроводностями и др. Это ослабление (затухание) подчиняется экспоненциальному закону и описывается след выражениями: по амплитуде 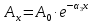 ; по интенсивности (частоте) ; по интенсивности (частоте) 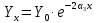 . . 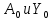 -начальные амплитуда и интенсивность колебаний; -начальные амплитуда и интенсивность колебаний;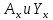 - амплитуда и интенсивность колебаний после прохождения волной в среде расстояния х; - амплитуда и интенсивность колебаний после прохождения волной в среде расстояния х; 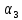 - амплитудный коэф затухания. Скорость предельных упругих волн явл наиболее употребительной характеристикой. Ее значение для различных ГП варьируется от 3,5 до 7 км/с, но иногда достигает 8,5 км/с. В осадочных породах она ниже 1,5-4,5 км/с. С ростом сжимающих нагрузок скорости упругих волн в ГП - амплитудный коэф затухания. Скорость предельных упругих волн явл наиболее употребительной характеристикой. Ее значение для различных ГП варьируется от 3,5 до 7 км/с, но иногда достигает 8,5 км/с. В осадочных породах она ниже 1,5-4,5 км/с. С ростом сжимающих нагрузок скорости упругих волн в ГП 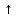 . .8. Реологические свойства горных пород. Реологические св-ва – характеризуют рост во времени деформ в ГП при постоянном напряжении (явление ползучести), либо падение напряжений при постоянной деформ (явление релаксации). Ползучесть и релаксация связаны с переходом упругих деформ в пластические, остаточные. До некоторого значения напряжения называемого пределом упругости данной породы, остаточные деформации в ней при кратковременной нагрузке не проявляются; протекающие деформации носят чисто упругий характер, и исчезают после снятия нагрузки. Если же значение напряжений превышают предел упругости, то на ряду с упругими деформациями происходят и пластические, сохр после разрушений испытываемых пород. Пластические св-ва могут быть охарактеризованы коэф пластичности, который представляет собой отношение работы, затрачиваемой на разрушение данного объема реальной породы к работе, необходимой для разрушения такого же объема породы, с теми же значениями предела упругости на сжатие в предложении идеальной упругости породы: 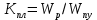 Если пластичность пород характеризует их поведение при напряжениях превышающих предел упругости, то ползучесть представляет собой медленное нарастание пластических деформаций и при напряжении меньшем предела упругости, но при достаточно длительном воздействии нагрузок. Явление обратное ползучести – релаксация напряжений. При релаксации упругих деформ ГП с течением времени переходят в пластические, но общая деформ во времени не изменяется, при этом происходит падение напряжений. Весьма сущ роль в проявлении необратимых деформ играют дефекты структуры материалов, поэтому реологические процессы в принципе можно рассматривать, как перемещение дефектов под действием внешних нагрузок, однако исключительная сложность определения молекулярных констант и разнообразие микроструктур реальных тв тел не позволяет в настоящее время применять ур-е связи между напряжением и деформ тел на микроскопическом уровне. Вследствие этого изучение деформ ГП во времени проводят в феноменологическом, микроскопическом уровне. Выражают взаимосвязи напряжений и деформ формализованных (не учитывающих реальных механических протекающих явлений) уравнениях механики сплошных сред. Весьма характерной чертой реологических процессов, в частности ползучести, является зависимость деформаций, наблюдаемых в данный момент времени от характера всего процесса нагружения материала (от всей предыдущей истории его деформ) – это св-во реальных материалов называют наследственностью. Особенностью большинства ГП, как показывают эксперименты, является практически линейная зависимость между приращениями деформ и приращениями напряжений в любой момент времени, т.е. проявление линейной ползучести. Это позволяет применять для описания деформ ГП во времени теорию деформ линейных наследственных сред. При этом полные деформ в любой момент времени слагаются из 2-ух составляющих: 1 - упругой деформации в момент приложения нагрузки 2 – собственной деформ ползучести. Математически это выражается: 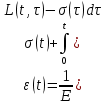 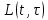 - выражает св-ва наследственности ГП. - выражает св-ва наследственности ГП. 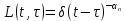 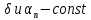 Реологические хар-ки являются пар-ми физический смысл которых в настоящее время не установлен. 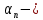 безразмерная величина; безразмерная величина; 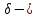 размерность « размерность «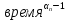 » »9. Модели деформирования ГП. Деформирование во времени м.б. математически описано путем обратного схематического представления ГП в виде некоторых модель из элементарных структурных единиц. Причем каждая из этих ед. представляет собой упругий, пластичный или вязкий элемент. При этом структурные ед. обладающие упругими св-вами м.б. представлены пружинами закона деформирования Гука: σ = E·ε, где σ-напряжение; ε-деформации; E-коэф. пропорциональности (модуль упругости). В случае объемного напряженного состояния з. Гука имеет вид: 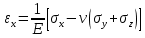 ; ; 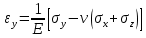 ; ; 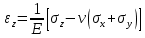 . .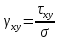 ; ; 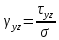 ; ; 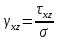 , где εx,εy,εz-линейное деформ. в направлении нормальных напряжений. , где εx,εy,εz-линейное деформ. в направлении нормальных напряжений. 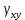 , ,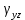 , ,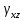 - деформации сдвига, ν-коэф поперечных деформаций. - деформации сдвига, ν-коэф поперечных деформаций.Структурные ед. с вязкими св-вами подчиняются з. деф. Ньютона σ=η 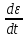 , где , где 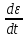 -скорость деформ.; η-коэф. вязкости. -скорость деформ.; η-коэф. вязкости. В модели они м.б. представлены поршнем со сквозными отверстиями в цилиндре с вязкой жидкостью. Пластические св-ва структурных ед. моделируют сухим трением. В этом случае деформирование может иметь место лишь при напряжениях, превышающих некоторое значение, наз. пределом текучести( 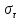 ) )Эксперименты показывают, что механизм пластической деформации связан со сдвигами материала по некоторым площадкам в связи с чем структурную схему жесткопластичной среды (жесткопластичная модель массива пород позволяет изучать его способность к пластическим [необходимым] деформациям, величина которых существенно превышает упругие деформации. в следствии чего последние во внимание не принимаются [сдвижение бортов карьеров]) можно представить в виде элемента трения. Структурная схема (рис.) φ-угол трения; k, σn·tgφ. Диаграмма напряжений. (рис.) из этой схемы => условие скольжения (условие Кулона-Мора) 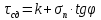 – касательные напряжения на площадках скольжения(1), где -угол внутреннего трения; k-сцепление (сопротивление сдвигу независимое от величины нормального давления); – касательные напряжения на площадках скольжения(1), где -угол внутреннего трения; k-сцепление (сопротивление сдвигу независимое от величины нормального давления);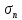 -нормальное напряжение на площадях скольжения; -нормальное напряжение на площадях скольжения;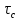 -касательное напряжение на площадях скольжения. -касательное напряжение на площадях скольжения.Если сдвигающие усилия < значения 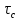 , то никаких деформаций не происходит. , то никаких деформаций не происходит.Условие (1) наз. условием предельного состояния. Оно положено в основу теорией предельного равновесия ГП. Условие (1) можно представить в виде огибающих наибольших предельных кругов напряжения (кругов Мора) (рис. а,б )(+еще 2 рис) Из графика а) => что условие предельного состояния реализуется на двух площадях наклоненных к наибольшему главному напряжению под углами (см. рис.б) 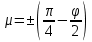 или или 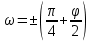 ω-угол наклона площадки скольжения к наименьшему σ3 главному напряжению. ω-угол наклона площадки скольжения к наименьшему σ3 главному напряжению.Эти площади называют площадками скольжения. Если некоторая область находится в предельном состоянии (во всех точках этой области выполняется условие предельного равновесия), то в ней можно провести поверхность скольжения, касательные пл-ти в каждой точке которых совпадают с площадками скольжения. Линии пересечения пов-тей скольжения с какой-либо пл-тью наз. линиями скольжения. (???рис.???) 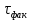 < < 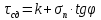 Из выше изложенного => что в условиях плоской задачи в области предельного равновесия можно провести два неортогональных семейства линий скольжения. Из выше изложенного => что в условиях плоской задачи в области предельного равновесия можно провести два неортогональных семейства линий скольжения.Из диаграммы, а) можно представить условие предельного состояния в главных напряжениях 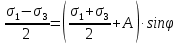 (2), где А = k·ctg (2), где А = k·ctg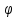 при при 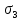 = 0 из этого уравнения получаем выражение для предела прочности материала(пород) при одноосном сжатии. = 0 из этого уравнения получаем выражение для предела прочности материала(пород) при одноосном сжатии.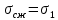 ; ; 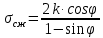 (3) Условие предельного состояния (2) можно представить в следующем виде: (3) Условие предельного состояния (2) можно представить в следующем виде: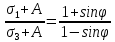 от сюда несложно получить еще один вид условия (прочности (пластичности) в главных напряжениях) предельного состояния от сюда несложно получить еще один вид условия (прочности (пластичности) в главных напряжениях) предельного состояния 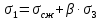 (4) (4) 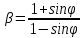 , - параметр объемной прочности. Условие (4) дает наглядное представление о возрастании сопротивления мат. пород в условиях объемного сжатия. , - параметр объемной прочности. Условие (4) дает наглядное представление о возрастании сопротивления мат. пород в условиях объемного сжатия.Пользуясь формулой напряжений 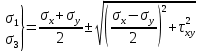 (5) и подставляя их в уравнение (2) получим выражение условия предельного сост. через компоненты напряжений в произвольной сист. координат. (5) и подставляя их в уравнение (2) получим выражение условия предельного сост. через компоненты напряжений в произвольной сист. координат. 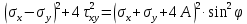 (6) (6) Условие предельного сост. (6) совместно с двумя дифференциальными уравнениями равновесия (для плоской задачи) 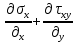 =0 ; =0 ; 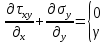 (7) (7) Соответственно в случае весомой и невесомой среды (ось у направлена вертикально) составляет полную систему уравнений для опред. 3 неизвестных компонентов напряжений, если известны напряжения на границе пластической области. В этом случае задача на опред. напряжений является статически определимой. Изображение упругих, вязких, пластических элементов м.б. представлено упругой моделью (тело Гука), вязкой моделью, моделью пластического тела, модели упруго-вязких тел. Большой значение при характеристике ГП имеет хрупкость – способность пород разрушаться под действием приложенных нагрузок без существенной остаточной (пластической) деформ. Хрупкость м.б. количественно характеризована коэф. хрупкости, который представляет собой отношение работы (Wy) затраченной на деформирование образца породы до предела упругости к общей работе (Wp) на разрушения данного образца. Кхр.= Wy/ Wp. Кхр для различных пород изменяется в весьма широких пределах. У упругих пород предел прочности приближается к пределу упругости. Проявление хрупкости ГП зависит от продолжительности действия силы. Динамические ударные нагрузки приводят породы к хрупкому разрушению тогда, как длит. приложение даже сравнительно небольших нагрузок может приводить к пластическим деформациям. Специфической хар-кой, часто используемой в геомеханике ГП явл. разрыхляемость – св-во породы занимать в разрыхленном состоянии больший объем по сравнению с тем, который она занимала в массиве. Показателем разрыхления служит коэф.разрыхления (Кр) , представляющий собой отношение объема Vp породы после ее разрыхления при обрушении или добыче к ее объему VM в массиве, т.е. до ее разрыхления 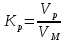 . Наименьшую разрыхляемость при прочих равных условиях имеют песчаные и глинистые породы. Кр=1.15-1.20, наиболее хрупкие скальные породы Кр=1.3-1.4 . Наименьшую разрыхляемость при прочих равных условиях имеют песчаные и глинистые породы. Кр=1.15-1.20, наиболее хрупкие скальные породы Кр=1.3-1.4С течением времени разрыхленные породы уплотняются, однако и после уплотнения они не достигают первоначальной плотности в массиве имевшей место до разрыхления. min Кр различных пород после уплотнения Кр=1.01-1.15 10. Структурные неоднородности породных массивов. Характерным св-вом ГП явл. высокая степень их неоднородности, которая обусловлена в первую очередь различием состава и строения пород. Более высокая степень неоднородности наблюдается в массивах, сложенных различными ГП, кроме того, в массивах часто встречаются геологические нарушения и несовместно развита естественная трещиноватость. Наконец в окрестности горных выработок массив интенсивно расчленяется искусственными (технологическими) трещинами, появление которых связанно с технологическими процессами ведения горных работ. В результате расчленения поверхностями указанных видов структурных неоднородностей массивы ГП имеют ярко выраженную блочную структуру. Причем размеры отдельных структурных блоков обычно существенно различаются между собой и опред. расстояниями между соседними поверхностями структурных неоднородностей. В существующих инженерно-геологических и горнотехнических классификациях исходя из размеров структурообразных блоков выделяют несколько порядков (классов) структурных неоднородностей. К неоднородностям нулевого порядка относят: крупные тектонические разрывы, связанные с региональными полями тектонических напряжений, разбивающие массивы пород на блоки с размерами >10км. Неоднородности первого порядка обусловлены наличием в массиве различных по составу, структуре и текстуре пород крупных геологических нарушений, тектонических разрывов и т.д. Эти неоднородности расчленяют массив на блоки от 100 м до километров. Более мелкие блоки от 10см до 10м связанны с неоднородностями второго порядка. К этому классу относят неоднородности структуры и состава пород в пределах одного слоя, а также естественную трещиноватость. Рассмотрим данный вид структурных неоднородностей. Трещины - разрывы в ГП, перемещение по которым совершенно отсутствует или очень незначительны. Совокупность трещин, расчленяющих тот или иной участок земной коры наз. трещиноватостью. В геологии трещины по времени их образования подразделяют: эндогенные (образ. в период формирования массива); экзогенные (появляются в результате послед. тектонических процессов) По степени проявления различают след. 3 группы трещин: 1. открытые; 2. закрытые; 3. скрытые. Открытые трещины имеют четко видимую полость, часто заполненную вторичными и гидротермальными материалами. Закрытые трещины характеризуется столь сближенными стенками, что, хотя сам разрыв по ним хорошо прослеживается, но полость по разрыву не заметна. Скрытые трещины, к которым часто относится кливаж углей, визуально не видно, т.к. они очень тонки, но их можно обнаружить при разбивании или дроблении ГП. Еще более мелкие блоки размерами до 10 см ограничиваются поверхностями неоднородностей третьего порядка. Они связаны с различием в химическом и минеральном составе, форме и размере зерен(кристаллов) с микротрещинноватостью. Наконец поскольку ГП в большинстве представляют собой многокомпонентные поликристаллические агрегаты, выделяют 4-ый порядок неоднородностей, связанных со структурными нарушениями межкристаллических областей, а также с дефектами структуры в решетке породообразующих минералов. Размеры структурных элементов колеблются от долей мм, до нескольких см. При этом необходимо подчеркнуть, что м/у выделяемыми порядками структурных неоднородностей в пределах того или иного массива ГП, как правило, наблюдается четкое соответствие. Кроме того, экспериментальные исследования показывают, что м/у геометрическими и механическими хар-ками структурных неоднородностей массивов также существует определенная связь: к крупным, но более редким поверхностям неоднородностей соответствует, как правило, более низкие значения прочностных характеристик. Естественно, что влияние неоднородностей различных порядков на деформирование или разрушение каких-либо объектов далеко неравнозначно. Например, неоднородности нулевого и первого порядка на устойчивость горных выработок практически не влияют, поскольку размеры структурных блоков определяются неоднородностями этих классов больше размеров выработок во много раз. В тоже время неоднородности второго порядка (в частности естествен. трещиноватость) оказывают на устойчивость выработок существенное влияние, обуславливая вывалы пород из стенок и кровли выработок. Степень влияния того или иного порядка неоднородностей определяется соотношением размеров соответствующих структурных блоков и геометрическим параметром деформирующихся объектов. При этом механизм деформирования массива пород блочной структуры заключается в деформировании самих блоков и кроме того их взаимном скольжении в вращении. Последнее, а именно скольжение в вращении блоков, может проявляться, если масштаб деформ. объекта соизмерим с размерами блоков, образуемых структурными неоднородностями того или иного класса, и они принимают участие в деформировании. Обобщенных численных показателей, характеризующих степень влияние структурных неоднородностей различных порядков на деформирование ГП и массивов, пока не имеется. Вместе с тем единичные эксперименты в породах различных петрографических разновидностей показывают, что с увеличением объемов, вовлекаемых в процесс деформир. модуле деформации массива снижаются, а величины деформаций возрастают. Различие показателей св-в ГП в зависимости от абсолютных геометрических размеров участков породного массива обусловлены появлением неоднородностей различных порядков наз. масштабным эффектом. Это прослеживается и при испытании образцов пород различных размеров. В большей степени изучено влияние поверхностей неоднородностей различных порядков на изменение прочностных характеристик массива ГП, являющиеся одним из проявлений масштабного эффекта. Поскольку при оценке устойчивости выработок, целиков, откосов бортов карьеров, часто возникает необходимость предрассчитывать прочность массива по данным испытаний образцов в лабораторных условиях, существенное значение имеет коэф. структурного ослабления (λi), представляющий собой отношение сцепления по контактам естественных трещин сцеплению в монолитной породе. Влияние других видов структурных неоднородностей на прочность массива изучено менее детально. Имеются лишь обобщенные данные о прочностных характеристиках, в частности, значения сцепления и углов внутреннего трения по контактам слоев различных осадочных толщ и отдельных петрографических наименований пород. 11. Св-ва пород массива в условиях естественного залегания. Св-ва пород в массиве существенно зависят от конкретных условий их залеганий, как геологических тел, степени неоднородности и анизотропности. На ряду со структурными неоднородностями в этом играют значительную роль многие другие факторы: мощность, характер и форма залегания породных тел с различными механическими св-вами и слоистость напластования; характер пород, окружающих рассматриваемое породное тело, в частности степень их жесткости или пластичности; тектоническое строение участка породного массива; степень выветренности, либо литифицированности пород; гидрогеологические условия рассматриваемых участков массива и т.д. Механическая неоднородность ГП одного петрографического наименования, т.е. изменчивость их механических характеристик от точки к точке связанна с непостоянством состава и строения. Степень неоднородности, обусловленная непостоянством строения связана с рядом факторов. Важнейшей структурно-геологической характеристикой участка массива (горно-геологических ярусов) являются тектонические условия залегания пород. Массивы пород (горно-геологические ярусы) могут быть подразделены на тектонически ненарушенные и тектонически нарушенные. Среди последних => выделить ряд типов: -с моноклинальным залеганием пород; -простого складчатого строения без разрыва сплошностей; -сложного складчатого строения с развитыми дислокациями, но без магматических включений; -сложного складчатого строения с вторичной складчатостью пород; -сложного складчатого строения интрузированные магматическими телами. Даже если основные механические хар-ки образцов пород, слагающие массивы различных типов близки м/у собой, св-ва таких массивов и поведение пород вокруг выработок м.б. существенно различными. Слоистость, напластование пород с различными механическими св-вами может обуславливать механическую анизотропность массива несмотря на то, что каждая из пород, слагающих толщу является по данным испытания образцов механически анизотропной. Эта анизотропность связанна с существенным различием механических св-в на контактах м/у слоями, пластами, слагающих толщу пород с различием св-в пород смежных слоев. Породы верхних слоев толщи обычно бывают в большей степени изменены процессами выветривания. В результате выветривания значит. нарушается монолитность породы, повышается степень трещинноватости. На контактах трещин часто присутствуют глинистые минералы – продукты выветривания, снижающие прочность и устойчивость участков массива при поверхностной зоне интенсивного выветривания пород. Породы нижних слоев осадочных толщ м.б. подвергнуты процессам литификации за счет уплотнения, обезвоживания, цементации продуктами выветривания выше лежащих слоев. В результате этих процессов породы одного вещественного состава и петрографического наименования на различных глубинах могут резко различаться по их св-вам, как в образцах, так и в соответствующих участках массива. Большое влияние на механическое влияние участков массива оказывает влажность пород. При испытании пород в образцах можно учесть влияние на их св-ва структурной, частично капиллярной и пленочной влажности, но нельзя определить степень влияния обводненности пород, т.е. свободной влаги, мигрирующей по трещинам. Обводненность приводит к снижению прочности пород в массиве и к их устойчивости в обнажениях. При деформировании пород такие пленки воды обволакивают поверхности вновь образованных трещин создавая расклинивающий эффект и способствуют дальнейшему развитию трещин. При различном росте глубины разработки существенное влияние на св-ва участков массива ГП могут оказывать увеличение температуры пород и повышение их растворимости как вследствие общего роста напряжений, а также ввиду роста физико-химической активности подземных минерализованных вод. Исключительно большое влияние на св-ва и поведение ГП в массиве оказывают условия и формы их залегания, а также взаимное расположение слоев с различными механическими св-вами. Изменчивые формы и невыдержанное чередование пород с различными механическими и плотностными св-вами обуславливают неравномерность распределения напряжений в массиве. Резко увеличивающиеся при проведении горных выработок. Большое различие в напряженность состояния пород и условий их деформировании вносит изменение залегания пород. Так при одинаковых механических хар-ках пород по данным испытания образцов их поведение вокруг выработок различно в зависимости от того проведены ли выработки в сводовых частях складок или в их синклинальных частях, или на крыльях. В первом случае обычно достигается максимальная устойчивость выработок. Одни и те же слои пород будучи расположены во вмещающих породах с различными св-вами ведут себя при деформ. совершенно различно. Так угольные пласты ведут себя как жесткие тела в толще пластичных глинистых пород, но пластически деформируются, если расположены в толще более жестких пород. Слои несвязанных сухих или малообводненных песков в толще пластически деформ. глин ведут себя как сплошные жесткие тела, но будучи обнажены немедленно проявляют сыпучие св-ва. 12. Гравитационное поле. Давление в тяготеющем шаре при постоянной плотности материала (см.рис.) Схема расчета вертикальных напряжений у поверхности Земли на глубине Н. 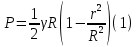 , где R-радиус шара; r-коорд. (расстояние от центра шара); , где R-радиус шара; r-коорд. (расстояние от центра шара);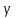 -объемный вес(плотность). -объемный вес(плотность).r=R-H; r1=R-H1. При подстановке r=R-H в (1) и пренебрежением величиной H2/R2 по сравнению с H/R имеем выражение для вертикального давления ГП на глубине H : p= 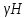 . На глубине H=400м при среднем объемном весе ГП . На глубине H=400м при среднем объемном весе ГП 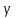 =2.5 тс/м3, р=1000 тс/м2 =100 кг/см2=10МПа. Данные полученные при изучении напряженного состояния верхней мантии со спутников Земли также указывают на величину напряжений 10МПа. Т.образом можно считать, что вертикальная составляющая гравитационного поля напряжений определяется из выражения: σ= =2.5 тс/м3, р=1000 тс/м2 =100 кг/см2=10МПа. Данные полученные при изучении напряженного состояния верхней мантии со спутников Земли также указывают на величину напряжений 10МПа. Т.образом можно считать, что вертикальная составляющая гравитационного поля напряжений определяется из выражения: σ=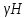 (2). (2). |
