геомеханика. 1. Геомеханика как раздел горной науки, основные понятия и определения
 Скачать 136.16 Kb. Скачать 136.16 Kb.
|
|
Оцениваем горизонтальные напряжения в нетронутом массиве. Рассмотрим в однородном изотропном упругом массиве элементарный объем в виде прямоугольного параллелепипеда. Пусть на его грани действуют нормальные сжимающие напряжения σx , σу , σz , а вертикальные напряжения σz= 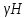 . Связь м/у деформ. и напряжениями описывается законом Гука : . Связь м/у деформ. и напряжениями описывается законом Гука : 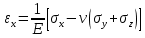 ; ; 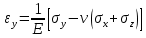 ; ; 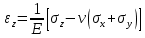 (3). (3).Если продолжить, что элементарный объем не деформируется в горизонтальном направлении, (рис)т.е. 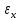 = =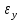 =0 и =0 и 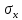 = =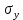 , то из выражения (3) => , то из выражения (3) => 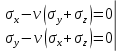 => =>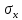 = =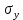 = =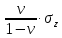 =λ =λ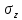 (4), λ-коэф. бокового давления по Динику. λ= (4), λ-коэф. бокового давления по Динику. λ=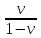 при при 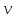 =0.25, λ=0.33 =0.25, λ=0.33При больших глубинах в результате релаксации напряжений напряженные состояния ГП стремятся к гидростатическому, т.е. λ=1. Коэф. бокового давления должен уточняться на основе экспериментальных исследований. 13. Тектоническое поле. В настоящее время связь высоких горизонтальных напряжений с зонами тектонических поднятий земной коры, происходящих в настоящее время или имевших место в прошлом, можно считать установленной. Поднятия земной поверхности могут быть связаны как с вертикальными, так и горизонтальными колебаниями земной коры. В районах опусканий и медленных погружений земной коры наблюдается гравитационное напряженное состояние, поэтому суммарные горизонтальные напряжения здесь могут быть меньше вертикальных. Следует отметить, что горизонтальные и вертикальные движения земной коры являются взаимосвязанными. Но поскольку к настоящему времени вертикальные перемещения лучше изучены, формирование полей тектонических напряжений связывается только с ними. В результате тектонических движений в недрах возникают активные силы сжатия, действующие в первом приближении горизонтально. Тектонические напряжения по своей величине превосходят гравитационные. Экспериментальные исследования на Кольском полуострове показали, что на глубинах 400-600м горизонтальные напряжения превышают вертикальные в 4-6 раз, т.е. λ=4...6. 14. Напряженные сост. водонасыщенного массива. ГП являются многоофазными средами, состоящими из тв. скелета и порового пространства, насыщенного жидкостью или газом. При оценке напряженного сост. в такой среде рассматриваются две системы давлений: Эффективные (pz) в скелете породы и нейтральные (pH) в поровой (среде) жидкости. Эффективные давления действуют на частицы, скелет, уплотняют породу. Нейтральные создают напор в жидкости, приводящий к фильтрации. Полное давление p: P=pz+pH (5). При P const. изменение pz и pH приводит к изменению другого давления. 15. Плоская и пространственная задачи НДС вокруг горных выработок. Арсенал механики ГП составляет теоретический, экспериментальные исследования, практическая оценка и корректировка полученных решений. НДС массива определяется путем решения краевых (граничных) задач механики ГП. Тип задач выбирается на основе реального деформирования массива и его свойств конкретных горно-геологических и горнотехнических условий. Так, например, при изучении распределения напряжений и деформирования вокруг выработок, проведенных в крепких породах с весьма незначительным проявлением свойств ползучести, может быть рассмотрена упругая задача. Технологические параметры (размеры выработки, место ее заложения и тип крепи и т.п.) устанавливаются путем сопоставления результатов решения задачи (напряжения или деформаций) с теми или иными критериями. При расчете целиков на прочность или давления на крепь рассматриваются упруго пластические задачи. Здесь предполагается, что в пределах всего целика или только его части ГП исчерпывают свою несущую способность и перестают сопротивляться внешним нагрузкам. Если выработка пройдена в слабых породах, где сильно проявляется действие фактора времени, необходимо решить задачи теории ползучести с учетом разрыхления ГП. При постановке задач следует учитывать изотропию (свойства не зависят от направления измерения) или анизотропию ГП (св-во зависит от направления измерения). Если свойства ГП одинаковы в различных точках они называются однородными. Слоистый массив в целом является неоднородным, породы в пределах слоя могут считаться однородными. Разброс мех св-в ГП оценивается коэф вариации: 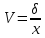 ; ; 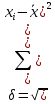 - средняя квадрат ошибка; - средняя квадрат ошибка; 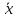 - среднее значение, - среднее значение, 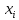 - значение измеренной величины, n – кол-во измерений. - значение измеренной величины, n – кол-во измерений.Коэф вариации механических свойств ГП колеблется в пределах 10-40% и более. Пространственная задача. НДС деформируемого тв тела в какой-либо точке полностью определяет тензоры напряжений и деформаций, каждая из которых состоит из 6-ти независимых компонентов. Геометрические уравнения связывают между собой компоненты тензора деформаций с 3-мя проекциями вектора смещения на оси координат. Таким образом решение задачи заключается в определении 15-ти неизвестных величин. Такая задача является пространственной. Методы решения пространственных задач отличаются большой сложностью и в настоящее время интенсивно разрабатываются. Можно выделить класс задач, допускающих значительное упрощение решения. Рассмотрим протяженную горную выработку (подготовительную, капитальную или длинный очистной забой) (рисунок. А – подготовительная выработка; Б – длинный очистной забой). Условия деформирования ГП в сечениях 1,2,3 значительно удалены от забоя выработки или штреков. Будут приблизительно одинаковыми, т.е. компоненты тензоров напряжений и деформаций в системе координат xyz, с осью z направленной вдоль оси выработки не будут зависеть от координаты z. В этих сечениях перемещения вдоль оси z будут равны 0. Деформации 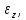 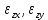 также можно считать равными 0. Количество неизвестных, подлежащих определению при решении задачи, уменьшается. Это напряжение - также можно считать равными 0. Количество неизвестных, подлежащих определению при решении задачи, уменьшается. Это напряжение - 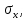 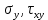 деформ деформ 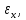 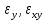 , смещение U и V. Напряжение , смещение U и V. Напряжение 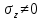 выражается через выражается через 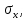 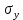 . Задачи такого типа называются задачами с плоской деформацией. . Задачи такого типа называются задачами с плоской деформацией.Если же рассматривать НДС тонкой пластинки, то можно пренебречь напряжениями, действующие в направлении ее толщины. Деформации в этом направлении, наоборот, 0 не равны, это задача с плоским напряженным состоянием. Плоская задача При решении плоских задач в механике ГП рассматривается протяженная горная выработка, проведенная в однородном (неоднородном) изотропном (анизотропном) горном массиве. Вертикальные сечения, нормальное к продольной оси выработки, представляет собой тяжелую полуплоскость с вырезом, соответствующим профилю поперечного сечения выработки. Это означает, что напряжения возрастают с увеличением глубины, по закону 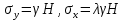 . .Рисунки а и б (расчетные схемы плоской задачи) На поверхности (границе полуплоскости) напряжение отсутствует. С достаточной степенью точности тяжелую полуплоскость с вырезом можно заменить весомой плоскостью с отверстием такой же формы, нагруженной на бесконечности (границах плоскости) сжимающими напряжениями, 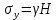 и и 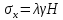 ; ; 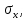 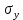 - вертикальная и горизонтальныая составляющие давления ГП в нетронутом массиве в центре намеченной выработки на глубине H (рисунок б). - вертикальная и горизонтальныая составляющие давления ГП в нетронутом массиве в центре намеченной выработки на глубине H (рисунок б).Указанные напряжения являются граничными условиями задачи. Найденные из решения значения напряжений должны на границе (на бесконечности в последнем случае) обращаться в известные. Другую группу граничных условий составляют условия на контуре выработки. Например, если выработки закреплена податливой крепью, то на контур выработки или на ее часть, действуют активные давления, соответствующие несущей способности крепи. 16.Расчетная схема задачи с плоским напряженным состоянием. Плоская задача При решении плоских задач в механике ГП рассматривается протяженная горная выработка, проведенная в однородном (неоднородном) изотропном (анизотропном) горном массиве. Вертикальные сечения, нормальное к продольной оси выработки, представляет собой тяжелую полуплоскость с вырезом, соответствующим профилю поперечного сечения выработки. Это означает, что напряжения возрастают с увеличением глубины, по закону 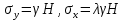 . .Рисунок а и б (расчетные схемы плоской задачи) На поверхности (границе полуплоскости) напряжение отсутствует. С достаточной степенью точности тяжелую полуплоскость с вырезом можно заменить весомой плоскостью с отверстием такой же формы, нагруженной на бесконечности (границах плоскости) сжимающими напряжениями, 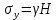 и и 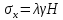 ; ; 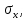 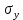 - вертикальная и горизонтальныая составляющие давления ГП в нетронутом массиве в центре намеченной выработки на глубине H (рисунок б). - вертикальная и горизонтальныая составляющие давления ГП в нетронутом массиве в центре намеченной выработки на глубине H (рисунок б).Указанные напряжения являются граничными условиями задачи. Найденные из решения значения напряжений должны на границе (на бесконечности в последнем случае) обращаться в известные. Другую группу граничных условий составляют условия на контуре выработки. Например, если выработки закреплена податливой крепью, то на контур выработки или на ее часть, действуют активные давления, соответствующие несущей способности крепи. 17. Основные уравнения плоской задачи теории упругости. Основные уравнения плоской задачи теории упругости. Уравнение равновесия в прямоугольной системе координат при пренебрежении массовыми силами: 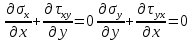 Геометрические уравнения: 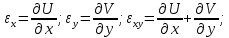 Физические уравнения однородной изотропной среды (закон Гука): 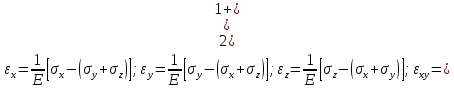 Т.к. в случае плоско-деформированного напряженного состояния z=0 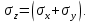 Подставив все получаем: 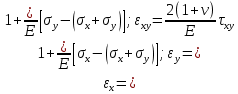 Приведем основные уравнения плоской задачи теории упругости в цилиндрической системе координат (рисунок) r, 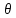 , z , zУравнение равновесия:  ; ;  Геометрические уравнения:  где U, V – перемещение вдоль радиуса r и к нему; r – радиальная деформация; - тангенсальная деформация; r - относительный сдвиг, где U, V – перемещение вдоль радиуса r и к нему; r – радиальная деформация; - тангенсальная деформация; r - относительный сдвиг,  -касательное напряжение. -касательное напряжение.При решении ряда задач удобно использовать функцию напряжений. Компоненты тензора напряжений выражаются через функцию напряжений следующим образом: 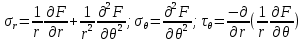 18. Горизонтальная выработка круглого профиля поперечного сечения в гидростатическом поле напряжений. Рассмотрим протяженную горизонтальную выработку круглой формы поперечного сечения, проведенную в однородном изотропном упругом горном массиве на глубине Н. Первоначальное напряженное состояние предполагается гидростатическим, λ=1. Напряжение в ненарушенном массиве в центре намечаемой выработки γН. Вертикальное сечение горного массива с выработкой, нормальное к её продольной оси, представим, как круглый вырез в невесомой плоскости со сжимающими напряжениями γН на бесконечности. (рис) Начальный радиус поперечного сечения выработки 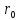 . На внутренний контур действует равномерно распределенные давления, моделирующие податливую крепь. Деформацией . На внутренний контур действует равномерно распределенные давления, моделирующие податливую крепь. Деформацией 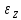 вдоль продольной оси выработки пренебрегаем, задача переходит в плоскую. Запишем граничные условия для радиальных напряжений вдоль продольной оси выработки пренебрегаем, задача переходит в плоскую. Запишем граничные условия для радиальных напряжений 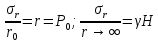 . Из симметрии задачи следует, что распределение напряжений и деформаций не зависит от угла . Из симметрии задачи следует, что распределение напряжений и деформаций не зависит от угла 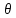 , а определяется только координатой r, т.е. все произведение по , а определяется только координатой r, т.е. все произведение по 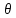 равно 0. равно 0.В этом случае уравнения принимают вид: 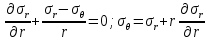 . А геометрические уравнения: . А геометрические уравнения: 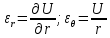 . Подставим физические уравнения: . Подставим физические уравнения: 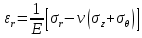 ; ; 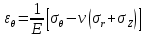 ; ; 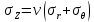 , получим: , получим: 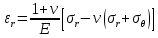 ; ; 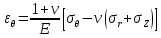 . Выразим деф . Выразим деф 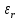 и и 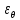 через перемещения: через перемещения: 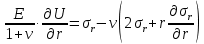 ; ; 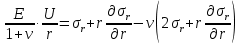 , Продифференцируем по r второе из уравнений и приравняем правые части этих уравнений. После простых преобразований получим ДУ: , Продифференцируем по r второе из уравнений и приравняем правые части этих уравнений. После простых преобразований получим ДУ: 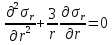 . Поскольку напряжения зависят только от r, последнее уравнение можно записать в виде обычных производных: . Поскольку напряжения зависят только от r, последнее уравнение можно записать в виде обычных производных: 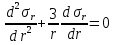 . . 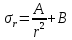 Постоянная интегрирование А и B определяется из граничных условий. Постоянная интегрирование А и B определяется из граничных условий. 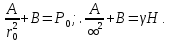 Из решения этой системы уравнений определим неизвестные: В= Из решения этой системы уравнений определим неизвестные: В=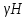 , А= , А=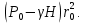 Напряжение Напряжение 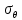 : : 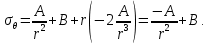 Таким образом получим следующие выражения для Таким образом получим следующие выражения для 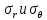 : : 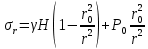 ; ; 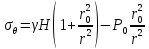 (см.рис). (см.рис).Распределение напряжений в массиве вокруг выработки В случае отсутствия крепи ( 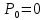 ) на контуре выработки ( ) на контуре выработки (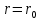 ) радиальные напряжения ) радиальные напряжения 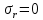 ,а тангенсальное ,а тангенсальное 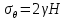 . .До проведения выработки напряжения в любой точке массива стали равны 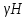 , так что в результате проведения выработки в массиве возникла концентрация напряжений. По мере удаления от контура выработки вглубь массива ( , так что в результате проведения выработки в массиве возникла концентрация напряжений. По мере удаления от контура выработки вглубь массива (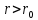 ) напряжения ) напряжения 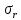 возрастают, а возрастают, а 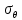 – уменьшаются. – уменьшаются.Зона повышенных напряжений вокруг выработки невелика. Уже на расстоянии, равном диаметру выработки от её контура ( 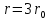 ), ), 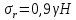 , , 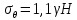 , т.е. напр отличаются от существовавших в ненарушенном массиве до проведения выработки , т.е. напр отличаются от существовавших в ненарушенном массиве до проведения выработки  на 10%. На расстоянии равном 2-м диаметрам от контура выработки 5 на 10%. На расстоянии равном 2-м диаметрам от контура выработки 5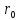 - это отличие - это отличие 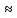 4%. Т.о. областью влияния выработки на напр состояние массива можно считать величину её диаметра. В случае выработки не круглого профиля поперечного сечения область влияния выработки – приблизительно её ширина. 4%. Т.о. областью влияния выработки на напр состояние массива можно считать величину её диаметра. В случае выработки не круглого профиля поперечного сечения область влияния выработки – приблизительно её ширина.Установка крепи в выработке 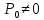 приведет к незначительному уменьшению концентраций напряжений у контура. Поскольку у реальных крепей приведет к незначительному уменьшению концентраций напряжений у контура. Поскольку у реальных крепей 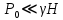 , смещение концентр напр весьма незначительно , смещение концентр напр весьма незначительно 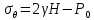 . . |
