геомеханика. 1. Геомеханика как раздел горной науки, основные понятия и определения
 Скачать 136.16 Kb. Скачать 136.16 Kb.
|
сцепление (сопротивление сдвигу независимое от величины нормального давления);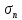 -нормальное напряжение на площадях скольжения; -нормальное напряжение на площадях скольжения;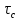 -касательное напряжение на площадях скольжения. -касательное напряжение на площадях скольжения.Если сдвигающие усилия < значения 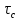 , то никаких деформаций не происходит. , то никаких деформаций не происходит.Условие (1) наз. условием предельного состояния. Оно положено в основу теорией предельного равновесия ГП. Условие (1) можно представить в виде огибающих наибольших предельных кругов напряжения (кругов Мора) (рис. а,б )(+еще 2 рис). Из графика а) => что условие предельного состояния реализуется на двух площадях наклоненных к наибольшему главному напряжению под углами (см. рис.б) 23. Расчет ползучести массива ГП. Важным фактором, влияющим на напряженно деформ состояние массива, является время. Опыт эксплуатации подземных сооружений показывает, что в случае их заложения в крепких породах и на малых глубинах, развивающиеся со временем деформации незначительны и по величине совпадают с упругими. При слабых боковых породах и на больших глубинах реологические процессы проявляются более интенсивно, деформации ползучести намного превосходят упругие, происходит растрескивание (разрыхление) ГП с последующим отделением от массива блоков различных размеров. В 1 случае, для прогноза поведения массива можно использовать теорию ползучести с малыми деформациями, Во 2-нужно учитывать большие деформации. Рассмотрим методы расчета ползучести ГП при малых деформациях Успехи теории ползучести ГП связанны с моделью наследственности, предполагающие, что деформации в любой момент времени зависит от всей предыдущей истории нагружения. Уравнение линейного деформирования наследственных материалов, авторов Больцмана-Вальтера, имеет вид: 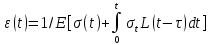 ; ; 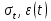 -деформационные напряжения в момент времени t от начала нагружения; -деформационные напряжения в момент времени t от начала нагружения; 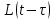 -ядро интегрального уравнения (ядро ползучести) вид которого зависит от свойства материала и определяется экспериментом; -ядро интегрального уравнения (ядро ползучести) вид которого зависит от свойства материала и определяется экспериментом;Ползучесть осадочных ГП удовлетворительно описывается уравнением с ядром ползучести типа Абеля: 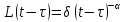 , где , где 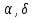 -параметры ползучести ГП; -параметры ползучести ГП;Для расчета небольших деформаций ползучести, разработали метод переменных модулей, заключающихся в замене в полученном упругом решении упругих соnst переменными модулями и проведении в дальнейшем алгебраических преобразований. При ядре ползучести типа Абеля, переменные модули имеет вид: 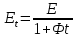 ; ; 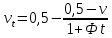 ; ; 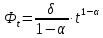 Рассмотрим в качестве примера плоскую задачу теории ползучести : из решения задачи для выработки круглого профиля поперечного сечения, тангенсальная деформация на контуре выработки можно записать: 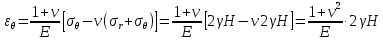 Т.е на контуре при отсутствии крепи: 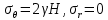 С другой стороны: 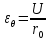 (на контуре). Таким образом смещение контура выработки имеет вид: (на контуре). Таким образом смещение контура выработки имеет вид: 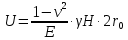 Заменим в упругом решении упругие const E и ν переменными модулями и получим выражение для смещения контура во времени: 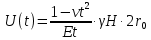 Напряжение в этой задачи отсутствующих const не зависят и поэтому по теории малых деформаций по времени не изменяется. Метод решения задач теории ползучести путем замены в решении задачи упругих const переменными модулями может применяется только в случае малых, т.е. соизмеримых с упругими деформациями ползучести. Расчет больших деформаций (для слабых ГП) снимают эти ограничения. Результат расчетов позволяет установить влияние основных горнотехнических факторов на смещение контура выработки и массива, а также изменение напряженного сост. массива. Смещение кровли, почвы и боков выработки во времени (вне зоны влияния очистных работ) носят затухающий характер и уменьшаются с увеличением несущей способности крепи Ро. (рис): 1)Po=0, 2)Po=0, 3)V, 4)U Смещение возрастает с увеличением глубины разработки и уменьшается с увеличением модуля упругости вмещающих пород. Коэф. Пуассона влияет на величину зоны деформации растяжения вокруг выработки. С увеличением коэф. бокового давления λ, вертикальные смещение уменьшаются, а боковые увеличиваются. 24. Критерии разрушения. Состояние горн выработок зависит не только от развивающихся в массиве упругих и не упругих (пластичность, ползучесть) деформаций, а также в значительной степени и от разрушения пород (зависит от разрушаемости пород). Выбор рациональных технологических решений по производству горн работ должен осуществляться только на основе знания механического состояния массива в полном объеме, т.е. с учетом разрушения пород. Под разрушением понимают разделение тела на части. При оценке разрушения в настоящее время используется представление о критических напряжениях или деформациях (классические теории прочности), либо рассматривается процесс накопления повреждений материала, определяемое длительностью напряжения (кинетических подход). 24.1 Классические теории прочности. 24.1.1 Теория мах нормальных напряжений. Предполагается, что разрушение наступает при достижении максимальным нормальным напряжением 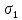 ,предельной величины ,предельной величины 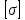 , определяемой экспериментально: , определяемой экспериментально: 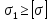 Критерий был выдвинут Галилеем, может применяться при одноосном деформировании (растяжение, сжатие) хрупких материалов. В случае неодноосного напряженного состояния, критерий использовать нельзя. Разрушение не произойдет при гидростатическом напряженном состоянии, это является одним из примеров. 24.1.2 Теория мах относительных линейных деформаций. Предполагается, что разрушение наступает при достижении наибольшей по величине линейной деформацией удлинения ( 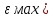 , предельной величины , предельной величины 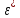 Закон Гука: 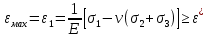 , где , где 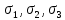 -главные напряжения; E-модуль упругости; ν-коэф. Пуассона -главные напряжения; E-модуль упругости; ν-коэф. ПуассонаТеория может применяться в некоторых случаях хрупкого разрушения: представления о предельных деформациях используется в настоящее время в кинетических теориях прочности. В частности, экспериментально установлено, что произведение скорости деформации на время до разрушения  24.1.3 Теория мах касательных напряжений Кулона-Треска. Разрушение наступает при достижении максимальной касательным напряжением предельной величины 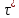 : : 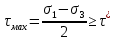 В качестве 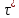 можно принять (1 можно принять (1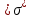 /2), где /2), где 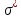 - предельное напряжение при растяжении.. Условие в этом случае примет вид: - предельное напряжение при растяжении.. Условие в этом случае примет вид: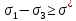 Критерий предложен Кулоном и может применяться для пластичных тел. 24.1.4 Энергетическая Теория. Разрушение наступает разрушение при достижении удельной энергии формоизменения некоторого предельного значения. Формоизменение связано с деформациями сдвига и касательными напряжениями: 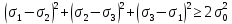 ; где ; где 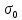 -const материала. -const материала.Эта теория справедлива для пластичных материалов. 25. Теория прочности Мора. Предполагается, что касательные напряжения на площадках скольжения, зависит от действующих тех же площадках нормальных напряжений. Разрушение происходит при достижении касательными напряжениями 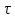 предедельной величины, зависящей от нормальных напряжений предедельной величины, зависящей от нормальных напряжений 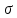 . .Считается, что промежуточное главное напряжение 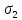 не влияет на процесс разрушения материала. Поэтому при оценке напряженного состояния строят только круги напряжения только для не влияет на процесс разрушения материала. Поэтому при оценке напряженного состояния строят только круги напряжения только для 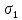 и и 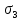 . .Экспериментально определяют предельные значения напряжений 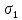 и и 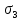 , приводящие к разрушению, и строят соответствующие круги напряжений, называемые предельными. , приводящие к разрушению, и строят соответствующие круги напряжений, называемые предельными.Для различных предельных кругов строят огибающую, касающуюся каждой окружности в точке. (рис. Предельные круги Мора: 1.-Одноосное растяжение,2.-одноосное сжатие,3.-двуоосное сжатие,4.-огибающая) Условие разрушения записывается в виде 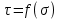 Вид функции 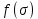 (огибающей) определяется экспериментально. (огибающей) определяется экспериментально.Огибающая предельных кругов Мора рассматривается как прочностная хар-ка материала. Разрушение наступает в случае, когда какой-либо круг напряжений коснется огибающей. Формы огибающей кривой, используемые в настоящее время в практических расчетах разнообразны: прямолинейная, параболическая, циклоидальная и др. Они определяются свойствами материала и его поведением в условиях различных напряженных состояний Рассмотрим наиболее простую форму огибающей - прямолинейную. Уравнение: 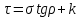 ; k-сцепление; ; k-сцепление; 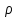 - уголвнутреннего трения - уголвнутреннего трения Для сыпучих сред: к=0, для пластичных: 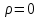 Значения К и 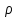 для тв горных пород занимают промежуточное положение(рис). для тв горных пород занимают промежуточное положение(рис).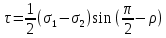 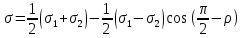 Подставив формулы, получим уравнение огибающей в главных: 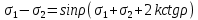 Разрушение происходит по площадке, составляющей угол 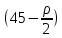 с напряжением с напряжением 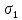 . Теория Мора позволяет описать переход материала из упругого состояния в пластическое, хрупкое и вязкое разрушения. Однако, неучет влияния промежуточного главного напряжения приводит к определенным погрешностям. . Теория Мора позволяет описать переход материала из упругого состояния в пластическое, хрупкое и вязкое разрушения. Однако, неучет влияния промежуточного главного напряжения приводит к определенным погрешностям.26. Теория квазихрупкого разрушения. В вершине трещины возникает значительная концентрация напряжений, поэтому при ее росте на ряду с разрывом связи между частицами вдоль берегов, происходят и пластические деформации в окрестности вершины. Но не учитывается теорией Гриффитса, это требует дополнительных затрат энергии. В концепции квазихрупкого разрушения Ирвина, для оценки прочности таких тел используется теория хрупкого разрушения, с учетом затрат энергии на пластические деформации. В этом случае в формулу Гриффитса вместо поверхностной “c” вводится эффективная поверхностная энергия: 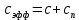 Где сп – удельная работа пластической деформации. Экспериментальные данные свидетельствуют о том, что 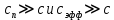 . .Теория квазихрупкого разрушения основана на анализе концентрации напряжений в окрестности трещины, которая определяется коэф. интенсивности напряжений К. Последние зависят от внешних нагрузок, формы тела, взаимного расположения трещин и определяются из решения упругой задачи. Рост трещин начинается при условии К=Кс, где Кс-const материала – вязкость разрушения. Трещины в теле в зависимости от характера действия внешних сил, могут развиваться в результате нормального разрыва продольного или поперечного сдвигов. (РИС) Для каждого из видов развития трещин определяются значения коэф. интенсивности напряжений К1, К2, К3, и вязкости разрушения К1с, К2с, К3с. Так, например, при растяжении пластины с трещиной нормального разрыва, длиной 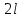 , напряжениями , напряжениями 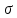 , коэф. интенсивности К1= , коэф. интенсивности К1=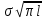 ; Кс1= ; Кс1=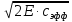 - вязкость разруш. - вязкость разруш.Условие разрушения: К1=Кс1 или 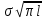 = =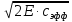 совпадают с формулой Гриффитса при замене «с» на «сэфф». совпадают с формулой Гриффитса при замене «с» на «сэфф».Величина вязкости разрушения определяется экспериментально, путем испытания образцов с трещинами. Для крепких ГП, типа песчаника, вязкость разрушения Кс1= 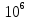 …1,5 …1,5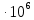 Н/ Н/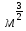 = (100…150)кгс = (100…150)кгс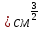 . .27. Кинетическая теория прочности. Кинетика процесса разрушения обусловлена развитием в теле под нагрузкой дефектов различного типа, накоплением повреждений. Для количественной оценки повреждаемости вводятся различные параметры. Кинетические теории в отличии от классических не рассматривают разрушение как пороговый (критический)процесс. Для условий одноосного напряженного состояния (растяжение напряжениями 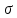 ) долговечность тела (время до разрушения) определяется термофлуктуационным уравнением прочности С. Н. Журкова ) долговечность тела (время до разрушения) определяется термофлуктуационным уравнением прочности С. Н. Журкова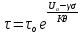 Здесь 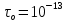 с, Uo – энергия активации, с, Uo – энергия активации, 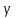 – активационный объем процесса разрушения, K – постоянная Больцмана, – активационный объем процесса разрушения, K – постоянная Больцмана, 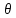 – абсолютная температура. – абсолютная температура.Долговечность ГП в условиях напряженного состояния изучена недостаточно. При оценке прочности сооружений приходится иметь дело с более сложным распределением напряжений. При использовании этой концепции разрушения необходимо знать, какая составляющая тензора напряжений или их комбинация определяют долговечность. В практических расчетах для оценки долговечности ГП используют: 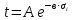 ; А и В константы, определяются опытным путем; ; А и В константы, определяются опытным путем; 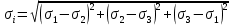 – интенсивность напряжений, – интенсивность напряжений, 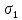 , ,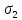 , ,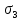 – главные напряжения. – главные напряжения. Выражение для долговечности справедливо лишь, при условии, что напряжения во времени не изменяются. При изменяющихся во времени напряжениях следует использовать принцип линейного суммирования повреждаемости: 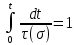 ; () -время до разрушения при постоянно действующем напряжении ; () -время до разрушения при постоянно действующем напряжении 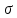 . .Если напряжение к действует на тело в течение промежутка времени tк, а затем изменяется, то: 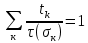 Эти выражения показывают, что при переменных нагрузках повреждаемость материала следует суммировать. Горная выработка некруглой формы профиля поперечного сечения. В горной практике широко применяются и другие формы профиля поперечного сечения, помимо круглой: прямоугольные, трапециевидные, арочные и др. В этом случае определить НДС массива вокруг выработки можно, если каким-либо способом математически преобразовать заданную форму профиля в круглую, решить известным методом задачу и снова перейти к исходному профилю. Некруглую форму профиля можно преобразовать в круглую с помощью конформных отображений. Эффективные методы решения задач математической теории упругости с применением конформных отображений принадлежит Г.В.Колосову и Н.И.Мусхелишвили. Метод конечных элементов (МКЭ). Метод Г.В.Колосова – Н.И.Мусхелишвили является эффективным при решении задач теории упругости, но его практическое применение связано с преодолением технических математических трудностей. Задача еще более осложняется при наличии нескольких выработок или неоднородного массива. В настоящее время, благодаря широкому применению ЭВМ, разрабатываются приближенно-численные методы решения задач теории упругости, вполне удовлетворительных для применения на практике одним из них является метод конечных элементов(МКЭ). Сущность метода заключается в представлении исследуемой области в виде набора элементов простой геометрической формы (прямоугольник или треугольник), характеризующейся упругими свойствами. (Рис) Элементы сочленяются в узлах, в них же удовлетворяются уравнения равновесия и совместимости деформации. Точность расчета повышается при увеличении числа расчетов (элементов). В результате определятся перемещения узловых точек вдоль осей координат и напряжений в центре тяжести элементов. МКЭ позволяет решать задачи о проявлениях горного давления с учетом конкретного горно-геол строения участка шахтного поля. С помощью компьютерных программ ЭВМ воспроизводится процесс формирования горного давления вокруг выработок, моделируется влияние основных факторов на устойчивость выработок. Вычислительные эксперименты на ЭВМ позволяют путем вариации параметров и учета конкретной обстановки выявить тенденции развития того лил иного процесса, разработать мероприятия по управлению состоянием массива. |
