геомеханика. 1. Геомеханика как раздел горной науки, основные понятия и определения
 Скачать 136.16 Kb. Скачать 136.16 Kb.
|
Рассмотрим теперь деформации массива вокруг выработки. 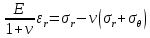 . Подставим выражение суммы напряжений . Подставим выражение суммы напряжений 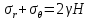 и получим: и получим: 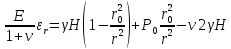 . . На контуре выработки при 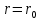 : : 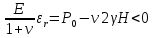 , т.к. , т.к. 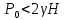 . В глубине массива при r . В глубине массива при r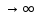 : : 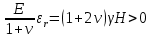 . Как видим, в радиальной деформации с удалением от контуров вглубь массива меняют знак: у контура они растягивающие, далее переходят в сжимающие. Таким образом у контура выработки образуется зона, в пределах которой горные породы испытывают деформации растяжения (см.рис).Координаты границ этой зоны . Как видим, в радиальной деформации с удалением от контуров вглубь массива меняют знак: у контура они растягивающие, далее переходят в сжимающие. Таким образом у контура выработки образуется зона, в пределах которой горные породы испытывают деформации растяжения (см.рис).Координаты границ этой зоны 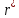 определяются из условия определяются из условия 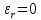 : : 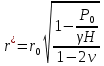 . В случае отсутствия крепи . В случае отсутствия крепи 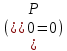 величина зоны растяжения зависит от коэф-та Пуассона и радиуса выработки: величина зоны растяжения зависит от коэф-та Пуассона и радиуса выработки: 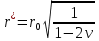 . .Меньшая зона растяжения образуется у пород с меньшим значением 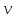 . Установка крепи приводит к весьма небольшому уменьшению этой зоны. . Установка крепи приводит к весьма небольшому уменьшению этой зоны.Образование зоны с деформациями растяжения у контура выработки (при сжимающих напряжениях у контура выработки, как показывают выше приведенные расчеты) создаёт необходимые условия для разрушения ГП. Поскольку они значительно слабее сопротивляются растяжению, чем сжатию. Размеры области растяжения превышают область возможного разрушения, но позволяют судить о порядке её величины. Существование такой зоны обнаруживается натурными наблюдениями на замерных станциях с глубинными реперами. 19. Горная выработка в негидростатическом поле напряжений. Рассмотрим НДС ГП вокруг протяженной, горизонтальной, круглой формы поперечного сечения выработки на глубине Н, при условии, что первоначальное напряженное состояние массива негидростатическое, т.е. коэффициент бокового давления λ 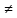 1 (рис.). 1 (рис.).Граничные условия: 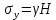 ; ; 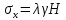 ; ; 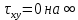 . . 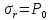 , , 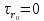 на контуре на контуре 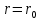 . Напряжения на бесконечности – главные. . Напряжения на бесконечности – главные. 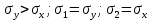 . Запишем их в цилиндрической системе координат . Запишем их в цилиндрической системе координат 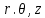 . Напряжение . Напряжение 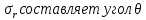 с осью с осью 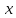 . Угол между осью . Угол между осью 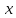 и площадкой, на которой действует и площадкой, на которой действует 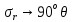 . В этом случае нормальные касательные напряжения выражаются через главные: (рис) . В этом случае нормальные касательные напряжения выражаются через главные: (рис) 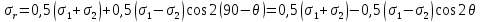 ; ; 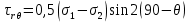 . Заменим . Заменим 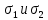 на на 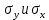 : : 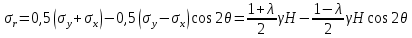 ; ; 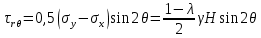 . Обозначим . Обозначим 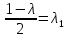 , , 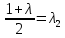 . Граничные условия на бесконечности примут вид: . Граничные условия на бесконечности примут вид: 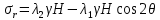 ; ; 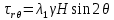 . Как видно –граничные условия представляют собой сумму постоянного давления . Как видно –граничные условия представляют собой сумму постоянного давления 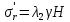 и переменного и переменного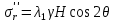 , завис-го от угла , завис-го от угла 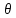 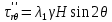 . В этом случае можно, используя принцип суперпозиции, разделить задачу на 2 части и решать их самостоятельно. . В этом случае можно, используя принцип суперпозиции, разделить задачу на 2 части и решать их самостоятельно.1-я задача для постоянного давления решена выше. Выражение для напряжений имеет вид: 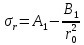 ; ; 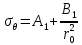 . .Решение 2-й задачи получается при использовании функций напряжений F. Поскольку напряжения зависят от 2-х координат r и 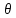 , функцию напр удобно представить в виде произведения функций r и , функцию напр удобно представить в виде произведения функций r и 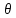 : : 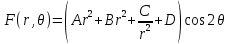 . Выразим компоненты тензора напряжений 2-й задачи через F: . Выразим компоненты тензора напряжений 2-й задачи через F: 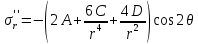 ; ; 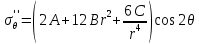 ; ; 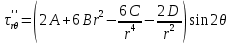 . Выражение для напряжений по 2-м задачам: . Выражение для напряжений по 2-м задачам: 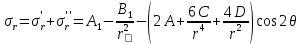 ; ; 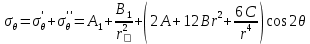 ; ; 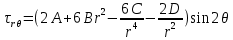 . Неизвестные коэффициенты . Неизвестные коэффициенты 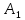 , , 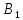 , А, В, С, Д определим, используя граничные условия. При r , А, В, С, Д определим, используя граничные условия. При r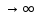 следует: следует: 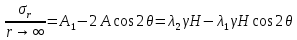 ; ; 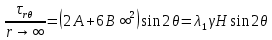 . Из этих выражений видно, что В=0, . Из этих выражений видно, что В=0, 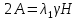 , , 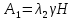 . . Воспользуемся теперь условиями на контуре выработки при 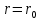 : : 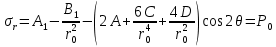 ; ; 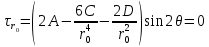 . Теперь определяем неизвестные коэффициенты: . Теперь определяем неизвестные коэффициенты: 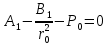 , , 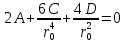 , , 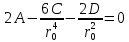 . Из 1-го уравнения из системы 2-х последних уравнений имеем: . Из 1-го уравнения из системы 2-х последних уравнений имеем: 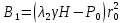 ; Д=- ; Д=-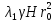 , 2С= , 2С=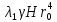 . Подстановка коэффициентов . Подстановка коэффициентов 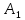 , , 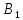 , А, В, С, Д в выражение дает следующее решение поставленной задачи: , А, В, С, Д в выражение дает следующее решение поставленной задачи: 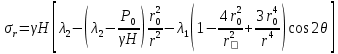 ; ; 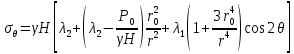 ; ; 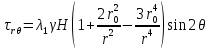 . В случае гидростатического напряженного состояния ( . В случае гидростатического напряженного состояния (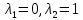 , , 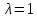 ) выражения переходят в решение задачи: ) выражения переходят в решение задачи: 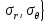 = =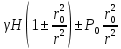 . Распределение упр деф ГП в массиве определяется по известным напряжениям и закону Гука. . Распределение упр деф ГП в массиве определяется по известным напряжениям и закону Гука.20. Паспорт прочности горной породы и его построение. Для количественной и качественной оценки поведения горных пород при различных видах напряженного состояния используют обобщенную характеристику, называемую паспортом прочности. В настоящее время общепризнано, что для построения паспорта прочности наиболее приемлемой является теория прочности Мора. В теории Мора постулируется, что ответственными за разрушение являются касательные напряжения, а само разрушение носит характер сдвига по площадкам, на которых достигается предельное состояние, причем величина предельного касательного напряжения является функцией нормального напряжения, действующего на площадке скольжения: Для характеристики напряженного состояния связь между σ и τ может быть представлена графически с помощью так называемых кругов напряжений, которые строят следующим образом. По оси абсцисс откладывают максимальное σ1 и минимальное σ3 значения главных напряжений, действующих на образец. На разности отрезков, как на диаметре, строится круг (рис. 4.6). 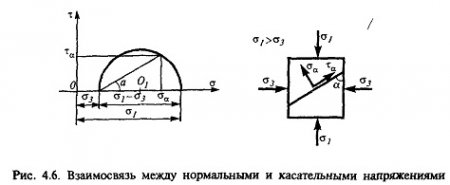 Этот способ изображения напряженного состояния характеризуется не только величиной главных напряжений σ1 и σ3, но и напряжениями σα и τα, действующими по произвольным площадкам, проходящим через рассматриваемую точку. Если напряжения σ1 и σ3 на которых построен круг Мора, достигают таких величин, что вызывают предельное напряженное состояние, при котором происходит нарушение сплошности, то соответствующий круг будет называться предельным. Все точки, лежащие внутри контура круга, указывают на то, что материал может выдерживать такое напряженное состояние, а за пределами его контура — свидетельствуют о разрушении. Если для нескольких разных видов напряженного состояния опытным путем получить предельные круги напряжений и нанести их на одну диаграмму, то все это семейство предельных кругов напряжений Мора имеет общую огибающую, которая состоит из двух ветвей, располагающихся симметрично относительно оси абсцисс. Эта симметрия обусловлена тем, что при всяком нормальном напряжении равновероятны два противоположно направленных касательных напряжения. На рис. 4.7 изображена огибающая, построенная к трем характерным кругам Мора: для одноосного растяжения, для одноосного сжатия и для неравномерного всестороннего сжатия. Предельный круг одноосного растяжения (1), соответствующий напряженному состоянию (σ1=σр; σ2—σ3=0), разместится слева от начала координат. Он пересечет ось σ в точках σр и 0. Предельный круг одноосного сжатия (II) таким же образом пересечет ось σ в точках 0 и σсж справа от начала координат. Предельный круг объемного сжатия (III) пересечет ось σ в точках σ1>0 и σ3>0. 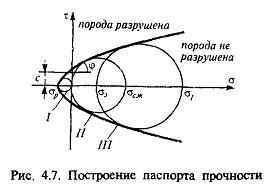 Можно построить сколько угодно предельных кругов, соответствующих условиям объемного напряженного состояния. Огибающая к предельным кругам характеризует напряженное состояние породы в момент ее разрушения и носит название паспорта прочности. Очевидно, что если круг исследуемого напряженного состояния пересечет огибающую, то такая комбинация напряжений вызовет разрушение, если он располагается под огибающей, то состояние разрушения еще не достигнуто. 21. Жестко-пластическая модель деформирования горных пород (теория Кулона-Мора). Пластические св-ва структурных ед. моделируют сухим трением. В этом случае деформирование может иметь место лишь при напряжениях, превышающих некоторое значение, наз. пределом текучести( 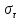 ) )Эксперименты показывают, что механизм пластической деформации связан со сдвигами материала по некоторым площадкам в связи с чем структурную схему жесткопластичной среды (жесткопластичная модель массива пород позволяет изучать его способность к пластическим [необходимым] деформациям, величина которых существенно превышает упругие деформации. в следствии чего последние во внимание не принимаются [сдвижение бортов карьеров]) можно представить в виде элемента трения. 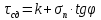 – касательные напряжения на площадках скольжения(1), где -угол внутреннего трения; k-сцепление (сопротивление сдвигу независимое от величины нормального давления); – касательные напряжения на площадках скольжения(1), где -угол внутреннего трения; k-сцепление (сопротивление сдвигу независимое от величины нормального давления);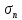 -нормальное напряжение на площадях скольжения; -нормальное напряжение на площадях скольжения;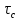 -касательное напряжение на площадях скольжения. -касательное напряжение на площадях скольжения.Если сдвигающие усилия < значения 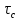 , то никаких деформаций не происходит. , то никаких деформаций не происходит.Условие (1) наз. условием предельного состояния. Оно положено в основу теорией предельного равновесия ГП. Условие (1) можно представить в виде огибающих наибольших предельных кругов напряжения (кругов Мора) (рис. а,б )(+еще 2 рис). Из графика а) => что условие предельного состояния реализуется на двух площадях наклоненных к наибольшему главному напряжению под углами (см. рис.б) 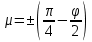 или или 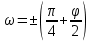 ω-угол наклона площадки скольжения к наименьшему σ3 главному напряжению. ω-угол наклона площадки скольжения к наименьшему σ3 главному напряжению.Эти площади называют площадками скольжения. Если некоторая область находится в предельном состоянии (во всех точках этой области выполняется условие предельного равновесия), то в ней можно провести поверхность скольжения, касательные пл-ти в каждой точке которых совпадают с площадками скольжения. Линии пересечения пов-тей скольжения с какой-либо пл-тью наз. линиями скольжения. (???рис.???) 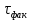 < < 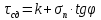 Из выше изложенного => что в условиях плоской задачи в области предельного равновесия можно провести два неортогональных семейства линий скольжения. Из выше изложенного => что в условиях плоской задачи в области предельного равновесия можно провести два неортогональных семейства линий скольжения.Из диаграммы, а) можно представить условие предельного состояния в главных напряжениях 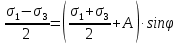 (2), где А = k·ctg (2), где А = k·ctg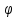 при при 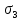 = 0 из этого уравнения получаем выражение для предела прочности материала(пород) при одноосном сжатии. = 0 из этого уравнения получаем выражение для предела прочности материала(пород) при одноосном сжатии.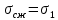 ; ; 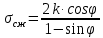 (3) Условие предельного состояния (2) можно представить в следующем виде: (3) Условие предельного состояния (2) можно представить в следующем виде: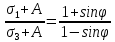 от сюда несложно получить еще один вид условия (прочности (пластичности) в главных напряжениях) предельного состояния от сюда несложно получить еще один вид условия (прочности (пластичности) в главных напряжениях) предельного состояния 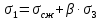 (4) (4) 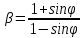 , - параметр объемной прочности. Условие (4) дает наглядное представление о возрастании сопротивления мат. пород в условиях объемного сжатия. , - параметр объемной прочности. Условие (4) дает наглядное представление о возрастании сопротивления мат. пород в условиях объемного сжатия.Пользуясь формулой напряжений 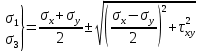 (5) и подставляя их в уравнение (2) получим выражение условия предельного сост. через компоненты напряжений в произвольной сист. координат. (5) и подставляя их в уравнение (2) получим выражение условия предельного сост. через компоненты напряжений в произвольной сист. координат. 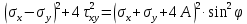 (6) (6) Условие предельного сост. (6) совместно с двумя дифференциальными уравнениями равновесия (для плоской задачи) 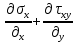 =0 ; =0 ; 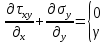 (7) (7) Соответственно в случае весомой и невесомой среды (ось у направлена вертикально) составляет полную систему уравнений для опред. 3 неизвестных компонентов напряжений, если известны напряжения на границе пластической области. В этом случае задача на опред. напряжений является статически определимой. 22. Пластическая модель деформирования горных пород (уравнение Кулона). Пластические св-ва структурных ед. моделируют сухим трением. В этом случае деформирование может иметь место лишь при напряжениях, превышающих некоторое значение, наз. пределом текучести( 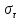 ) )Эксперименты показывают, что механизм пластической деформации связан со сдвигами материала по некоторым площадкам в связи с чем структурную схему жесткопластичной среды (жесткопластичная модель массива пород позволяет изучать его способность к пластическим [необходимым] деформациям, величина которых существенно превышает упругие деформации. в следствии чего последние во внимание не принимаются [сдвижение бортов карьеров]) можно представить в виде элемента трения. Структурная схема (рис.) φ-угол трения; k, σn·tgφ. Диаграмма напряжений. (рис.) из этой схемы => условие скольжения (условие Кулона-Мора) 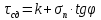 – касательные напряжения на площадках скольжения(1), где -угол внутреннего трения; k- – касательные напряжения на площадках скольжения(1), где -угол внутреннего трения; k- |
