В.Ю. Соколов К ВОПРОСУ О РЕЛАКСАЦИИ НАПРЯЖЕНИЙ В ГОРНОМ МАССИВЕ. Массива вокруг выработки

• Название: Массива вокруг выработки
• Дата: 06.03.2022
• Размер: 47.55 Kb.
• Имя файла: В.Ю. Соколов К ВОПРОСУ О РЕЛАКСАЦИИ НАПРЯЖЕНИЙ В ГОРНОМ МАССИВЕ .docx
• Тип: Документы; #385082
• страница: 1 из 4

УДК 622.831.31.622.363.2
В.Ю.СОКОЛОВ

Пермскийгосударственныйтехническийуниверситет
К ВОПРОСУ О РЕЛАКСАЦИИ НАПРЯЖЕНИЙ В ГОРНОМ МАССИВЕ В ОКРЕСТНОСТИ ВЫРАБОТКИ
Приведена численная реализация моделей наследственности и старения в задаче об изменении во времени напряженно-деформированного состояния соляного массива вокруг выработки.
Рассмотрим задачу о напряженно-деформированном состоянии (НДС) однородного изотропного массива соляных пород вокруг оди- ночной протяженной цилиндрической выработки глубокого заложения в условиях гидростатического распределения напряжений в ненару- шенном массиве (λ=1).

Введем цилиндрическую систему координат r, φ, z. Если ось z со- вместить с продольной осью выработки, сечения породного массива, нормальные к оси z, будут находиться в состоянии обобщенной пло- ской деформации.

На глубине H компоненты начального поля напряжений (до про- ведения выработки) следующие:
⁽⁰⁾  ⁽⁰⁾  ⁽⁰⁾  H; ⁽⁰⁾  ⁽⁰⁾  ⁽⁰⁾  0 . (1)

z r  rz r z
Соответствующее ему начальное поле деформации имеет вид:

_(0) _{ }(0) _{ }(0) _{ 0 ; }( 0)
_{ }( 0)
_{ }( 0)

 ^H(1  2) , (2)

rz r z

z  r _E

где γ  средний предельный вес вышележащих пород; µ

• 
  коэффициент Пуассона; Ε– модуль упругости.
  

Проведение выработки в момент t=0 вызывает возмущение на- чального поля напряжений: на компоненты напряжений (1) наклады- ваются дополнительные напряжения, вызванные проведением выра- ботки:

_УП _{ }(0) _{ }(У) <sub>;

</sub>УП _{ }(0) _{ }(У) _{; }УП

 ⁽⁰⁾  ^(У) . (3)

z z z

  

r r r

Дополнительные напряжения и соответствующие им дополни- тельные деформации определяются в начальный момент (t=0) упруги- ми свойствами массива и находятся из известного решения задачи Ла- ме:

_(У) _{ } ^H

; ^(У)  ^H; ^(У)  (^(У)  ^(У) )  0 ; (4)

r _r2  _r2 z r 

_(У)

_{ } 1   H_;

^(У)  ^{1  H}; ^(У)  0 . (5)

r _{E r2} 

E r^{2 z}

Полные упругие напряжения при этом будут:
^УП  ^  ^{1 } ; ^УП  ^  ^{1 } ; ^УП H. (6)


H1
_r  _r2  _ ^H¹ _r2  _z

   

Здесь через rобозначена радиальная координата, отнесенная к

начальному радиусу выработки

R₀ . Полю полных упругих напряжений

соответствует по закону Гука поле полных деформаций:
^УП ^H(1  2)  ^{1   H}; ^УП ^H(1  2)  ^{1   H};

^r E E r^{2  E E r2}


^УП ^H(1  2)

z _E

(7)

и соответствующее поле полных смещений массива.

В последующие моменты времени t>0 напряженно- деформированное состояние массива пород определяется нелинейны- ми соотношениями теории наследственной ползучести [1]. Образуются новые поля напряжений и деформаций, обусловленные реологически-

ми процессами в массиве. Поле полных деформаций  ^Попределяется

полем полных напряжений  ^Пи зависит от времени:

^П ^УП (t) ; ^П

 ^УП (t) ; ^П

 f_^П_ 

f^_^УП (t)^_ . (8)

Такая расчетная схема, однако, как справедливо отмечает И.В. Родин [2], давала бы неверные оценки для распределения смещений в окрестности горной выработки, поскольку наблюдаемые в породном массиве механические процессы при производстве горных работ свя-

заны с формированием лишь дополнительных деформаций и, соответ- ственно дополнительных смещений.

В том случае, когда деформации и напряжения связаны линей- ным законом Гука, деформации и смещения, вызванные проведением выработки, могут быть выражены через дополнительные (снимаемые) напряжения. Термин «снимаемые напряжения» (снимаемое поле на- пряжений) предложен И.В. Родиным и характеризует физический смысл дополнительных напряжений. Действительно, образование вы- работки означает, что с контура ее сечения как бы снимаются напря- жения (нормальные и касательные к контуру), действовавшие в нена- рушенном массиве. Таким образом, реальное поле деформаций и, со- ответственно, смещений будет определяться выражением (5), а не (7). Тот же результат получится, если из поля полных упругих деформаций

^УПвычесть начальное поле ⁽⁰⁾ (2). Такой подход будет справедлив и в

случае породного массива, подчиняющегося нелинейному физическо- му закону деформирования (8) и [1].

В математической постановке задачи, излагаемой ниже, под де- формациями и напряжением понимаются их полные значения.

Для сформулированной выше задачи имеем уравнения равнове- сия и совместимости деформаций:

^r ^{r }  0,

r r
(9)

_{ } _r _

r r
 0 . (10)

Уравнения состояния породного массива [1] запишутся в виде:

₁  ^t

_r   _2G(_r )  _ K_c[t , _i](_r )d_ ;

 0 
₁  ^t

_    _2G(_  )  _ K_c[t , _i](_  )d_ ; (11)

 0 

₁  ^t

  _{3B }  _ K_v[t , _i]d_ , (12)

где   ¹ (    

 0 

) ; G ^E ;   ¹ (     ) ; B ^E .

₃ r  z

2(1  )

₃ r  z

3(1  2)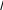

c э oc c э
Ядра интегральных уравнений (11) и (12) или функций скоростей сдвигов и объемной ползучести принимаем в виде [1]:

K[t, ,  ()]  

exp_b[ () 

]^nc_(t )^ , (13)

сж
K[t, ,

()]  

exp_b[

() 

]^nv1_(t )^ , (14)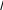