В.Ю. Соколов К ВОПРОСУ О РЕЛАКСАЦИИ НАПРЯЖЕНИЙ В ГОРНОМ МАССИВЕ. Массива вокруг выработки

• Название: Массива вокруг выработки
• Дата: 06.03.2022
• Размер: 47.55 Kb.
• Имя файла: В.Ю. Соколов К ВОПРОСУ О РЕЛАКСАЦИИ НАПРЯЖЕНИЙ В ГОРНОМ МАССИВЕ .docx
• Тип: Документы; #385082
• страница: 2 из 4

v э ov c э

сж
где  ,

_oc,

_ov, b_c,

b_v,

n_c, n_v

- параметры сдвиговой и объемной пол-

зучести;

_сж  предел прочности породы на одноосное сжатие при

«мгновенном» нагружении. Безразмерный параметр  будем считать постоянным и примем равным 0,7 [3].




э
В качестве эквивалентного напряжения для соляныx пород

можно принять интенсивность напряжений или обобщенное напряже- ние [4]: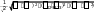

_i  ,

где ₁ , ₂ , ₃  главные напряжения.

Параметры ядер сдвиговой и объемной ползучести представляют собой параметры формальной аппроксимации кривых сдвиговой и объемной ползучести. Если же параметр  принять постоянным, то остальным параметрам можно приписать на феноменологическом уровне некоторый физический смысл.

Соотношения (11) и (12) описывают активную наследственную деформацию соляных пород в случае, когда нелинейность обусловлена исключительно влиянием фактора времени. Для каждого момента вре- мени t> 0 будет свой (нелинейный) закон связи между напряжениями и деформациями.

Процессы, соответствующие нагрузке в прямом смысле слова, т.е. уменьшение деформации при уменьшении напряжений, уравнения

(11) и (12) не описывают. Заметим, что процесс релаксации не является процессом разгрузки, и делать специальные предположения о законе разгрузки при этом не нужно [5].

Заметим, что уравнение (12) описывает не объемную ползучесть, а трещинообразование в процессе ползучести, сопровождающееся из- менением объема. При этом разрушающееся тело ведет себя как на- следственно-упругое с объемной наследственностью [5], [1].

В системе пяти уравнений (9)(12) независимы лишь пять неиз-

вестных функций координаты rи времени t:

_r,

_ ,

_z,

_r,

_ . Вели-

чина  _zявляется известной постоянной, равной _z

 ^H(1 2) .

E

В результате достаточно громоздких, но элементарных преобра- зований система (9)(12) приводится к одному нелинейному интегро- дифференциальному уравнению относительно _r:
d² 3 d ^t_

₂^r^r _ F(t )

d  0 , (15)

dr rdr ₀
где функция Fс учетом принятых выражений для ядер интегральных операторов (13)(14) имеет вид:

^{1 } <sup>  d d2  2 

d</sup> 2^

F  _exp(bⁱ) ^3^r r^r

_z _{ }

(1)r

^{oc c} ^ dr

^{2 } 3 dr 3 

_ cж _

dr _{ }

_^{d }_i^<sup>12

d</sup>_r^{2 }^

_drexp(b_c )_{  3}

(_r_z)  r_{dr3 }

 сж  _<sup>

1</sup> ^{  1 2 d d2 d }

(16)

• 
   _exp(bⁱ)
  

_3r_{ r}r_z_

(1)r

ov v_

3 ^ dr

² dr^

_ cж

_d^{ }_i^12

_ dr _

^d_r^

_drexp(b_v )_{ 3} (2_r.  r_dr_z)_.

^{ cж  }

Граничные условия задачи имеют вид:
_r 0 при r 1 (на контуре выработки), _r H

при r  . (17)

Значения неизвестных величин выражений:

_ ,

_z,

_r, _

определяются из

_  _r

 r^dr , (18)

dr

  2 r<sup>dr t

1</sup>exp(b

^i)(2 r^dr2 ) 

z r _dr



^{  }oc c r



_0 3 _cж dr

d ^
z
(19)

 exp(bⁱ)(2 r^r )_*(t)^d E⁽⁰⁾,




ov v r

cж

_dr z z

   1 ^t

  ^rz 

exp(b ^i )(  

)(t )^ d , (20)

0
^r 2G 2G^



oc c r z

cж

  ^{  z} ¹ t 

exp(b ^i )(  

)(t )^ d . (21)

0
^ 2G 2G^

oc c  z

cж


При этом в выражениях для деформации исключены их началь- ные значения, соответствующие напряженному состоянию нетронуто- го массива.

Решение уравнения (15) с граничными условиями (17) осуществ-

лялось методом шагов по времени [6]. Промежуток времени [0, t] раз-

бивается на части точками

t_s(s 1, 2, 3,...) . Значения

_r(r, t) ,

 _z(r, t)

представились последовательностями функций ^s, ^s. При этом инте-

r z

грал по времени записывается в первой части уравнения (15) и после применения формулы интегрирования по частям заменяется квадра- турной формулой вида
t

P _ F()(t )^ d 

0

^{N } (t t

₎1

(t t)^1

F(t)  F(t )

^  _