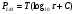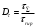Статья по лопаткам оформленая. Статья. 1. Статическое разрушение 3 Метод исследования
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
СодержаниеВведениеДетали турбин, в особенности лопатки, длительно работают в условиях неравномерного нагрева при высоких температурах, при этом характеристики материала в процессе эксплуатации изменяются. При расчетах напряженно-деформированного состояния (НДС) и прочности необходимо учитывать вязкопластическое деформирование и ползучесть материала. Современные методы расчетов, в том числе конечно-элементные, позволяют проводить расчеты лопаток турбин с использованием данных о физически нелинейных свойствах материала, включая ползучесть. Статическое разрушение — одна из наиболее частых причин выхода деталей турбин из строя, поэтому задача прогнозирования долговечности деталей турбин является актуальной. В данной работе описывается способ расчета кинетики НДС для изотропных сплавов. Монокристаллические сплавы предлагается рассматривать как изотропные со свойствами, соответствующими кристаллографической ориентации. Это допущение достоверно для зон пера лопатки, так как направление основных напряжений совпадает с радиальным. Для зон трактовых и бандажных полок такое допущение может привести к большим ошибкам в определении НДС, поэтому в дальнейшем планируется разработать метод, в котором будет учтена анизотропия характеристик ползучести. 1. Статическое разрушениеСтатическое разрушение — одна из наиболее частых причин выхода деталей турбин из строя, поэтому задача прогнозирования долговечности деталей турбин является актуальной. В данной работе описывается способ расчета кинетики НДС для изотропных сплавов. Монокристаллические сплавы предлагается рассматривать как изотропные со свойствами, соответствующими кристаллографической ориентации. Это допущение достоверно для зон пера лопатки, так как направление основных напряжений совпадает с радиальным. Для зон трактовых и бандажных полок такое допущение может привести к большим ошибкам в определении НДС, поэтому в дальнейшем планируется разработать метод, в котором будет учтена анизотропия характеристик ползучести. Как правило, деталям турбин свойственно сложное термонапряженное состояние, значения температур и напряжений изменяются в широких диапазонах. В то же время для проведения расчетов необходимы характеристики ползучести, описывающие поведение материала лопатки во всем рабочем диапазоне условий эксплуатации. Явление ползучести — это нелинейное изменение во времени деформаций (собственно ползучесть) и напряжений (релаксация), возникших в начале приложения нагрузки. Выделяют несколько стадий ползучести: неустановившаяся ползучесть — на этой стадии происходит упрочнение и скорость ползучести уменьшается; установившаяся ползучесть — процессы упрочнения и разупрочнения находятся в равновесии, скорость ползучести постоянна; разупрочнение и разрушение — скорость ползучести возрастает. Форма и вид кривой ползучести зависят от сплава, параметров режима испытаний и определяются несколькими конкурирующими механизмами (упрочнение, разупрочнение, разрушение). На рис. 1 представлена характерная кривая ползучести с обозначенными стадиями ползучести и начальной деформацией el, деформацией ползучести сr, временем нагружения (ч) и минимальной скоростью ползучести ecr(min).  Рисунок 1 - Типичная кривая плзучести В программном комплексе ANSYS предложены 13 уравнений неявной ползучести, такие, как уравнение Нортона, Гарофало (описывают установившуюся ползучесть) и уравнения, соответствующие гипотезам упрочнения и течения. Также возможно использование изохронных кривых. Несмотря на большой выбор, при расчетах кинетики НДС возникают следующие трудности. ввиду сложности кривой уравнения описывают только первую и вторую стадии ползучести; подбор коэффициентов для всего диапазона температур и напряжений, а также согласование значений коэффициентов между ними зачастую сопряжено с большими трудностями, и адекватность аппроксимации возможна только для узкого диапазона напряжений и температур; изохронные кривые неприменимы для расчетов со ступенчатым изменением нагрузки. Необходимо отметить, что единая теория, описывающая поведение материала во всем диапазоне значений температур и напряжений, в настоящее время отсутствует. Это связано с тем, что при изменении внешних параметров нагружения изменяется сам механизм пластической деформации. В то же время существует ряд моделей, отвечающих определенным диапазонам параметров и условий, хорошо совпадающих с экспериментальными данными. Задача теории ползучести применительно к одноосному напряженному состоянию заключается в установлении связи между напряжением, деформацией, скоростью, температурой, временем и целым рядом структурных параметров, характеризующих состояние материала в любой текущий момент времени вплоть до разрушения. В данной работе исследован и разработан способ расчета кинетики НДС, при котором используют данные, подвергнутые минимальной обработке; он позволяет рассчитывать все три стадии ползучести. Таким образом достигают повышения точности прогнозирования расчетной долговечности и изменения геометрии деталей турбин в процессе работы. 2. Метод исследования.Использован метод, описанный в работе, который основан на подобии кривых зависимости пределов длительной статической прочности и пределов ползучести от параметра Ларсона — Миллера. Это параметр рассчитывают по формуле
где С — постоянная, равная, как правило, 20; T — температура материала, K; — продолжительность нагружения, ч. На рис. 2 показаны зависимости пределов ползучести для заранее определенных значений деформаций и кривая предела длительной прочности dl. Для построения кривых Ларсона — Миллера желательно использовать более 5–7 значений деформаций. Наличие изломов этих кривых объясняется изменением характера разрушения. В ANSYS возможно применение пользовательской модели ползучести с помощью подпрограммы USERCREEP, написанной на FORTRAN. В этом случае необходимо вычислить за расчетный шаг времени Δ приращение деформации cr и двух дополнительных параметров, которые используются при расчете тангенциальной матрицы жесткости. Эти параметры характеризуют чувствительность приращения деформации ползучести к текущему напряжению d(cr)/d() и деформации d(Δcr)/d(cr). Также можно определять дополнительные результаты: повреждаемость и остаточную долговечность, которые по умолчанию не вычисляются и не сохраняются в процессе работы. С этой целью пользователю предоставляется массив Ustatev. Кривые Ларсона — Миллера (см. рис. 2) применяют для построения условной кривой ползучести по действующим напряжениям Мизеса и температуре T, °C, во всех точках интегрирования конечно-элементной модели. В дальнейшем эта кривая используется для расчета приращения деформации cr и/или повреждаемости D. Таким образом, предлагаемый способ расчета кинетики НДС дает возможность инженеру рассчитывать отклик, исходя из выбираемой им в препроцессоре гипотезы ползучести: модель течения, упрочнения или модель, критерием которой является накопленная повреждаемость. 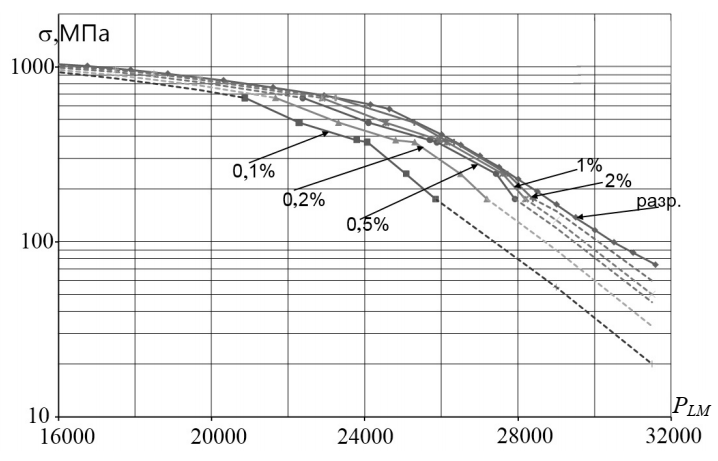 Рисунок 2 - Параметрические кривые Ларсона — Миллера для разрушения Верификацию предложенных методик проводили по результатам испытаний рабочей лопатки турбины высокого давления в течение 115 ч в ОАО “Авиадвигатель”. Результаты испытаний были переданы автору для изучения. Лопатка (рис. 3, а) была смоделирована совместно с диском с помощью гексагональных и тетраэдральных элементов второго порядка. Для учета взаимодействия в замковом соединении и монтажного натяга между бандажными полками были использованы 3Dконтактные элементы. Поле температур задавали постоянным по сечению лопатки, распределение температур по длине лопатки представлено на рис. 3, б. Расчет проведен с учетом нелинейных свойств сплавов и геометрической нелинейности. Использовав предложенный способ определения кинетики НДС, проведен сравнительный анализ расчетной и экспериментально измеренной остаточной вытяжки бандажной полки (по зонам 3 и 8, рис. 4) и адекватности оценки расчетной долговечности.  Рисунок 3 - Твердотельная модель (а) и распределение температуры по перу Для расчета повреждаемости использованы эквивалентные напряжения [7]. Под эквивалентными понимают некоторые условные напряжения, которые постоянно действуют в течение всего рассматриваемого времени работы и приводят к повреждаемости, равной повреждаемости, получаемой истинными изменяющимися во времени напряжениями; последние определяли на каждом интервале времени:
где m(T) — показатель статической прочности; — текущее время; — время нагружения. Статическую повреждаемость вычисляли как отношение
где rup — время до разрушения при действующем напряжении m. Повреждаемость равна нулю для нового изделия и единице при разрушении. 3. Сравнение результатов экспериментальных и численных исследований. Эксперимент прерывался каждые 15…40 ч для замера деформации и оценки состояния, он был остановлен через 115 ч ввиду большой деформации бандажной полки. Расчеты были остановлены через 100 ч ввиду проблем со сходимостью. Каждый узел лопатки исследован для определения опасных зон лопатки (18 на рис. 4). Также на рис. 4 представлено поле напряжений Мизеса, МПа. В таблице приведены результаты расчета НДС, величины накопленных за 100 ч работы деформаций cr, %, и длительной статической повреждаемости лопатки Dτ. Также представлены значения температур T, °C, первоначальных напряжений σ0, МПа, и отношение Dτ**/Dτ, где Dτ и Dτ** — повреждаемости без учета и с учетом явления ползучести.  Рисунок 4 - Поле напряжений по Мизесу, МПа, (а) с указанием опасных зон 1 — галтель между рабочей и соседней гранями бандажной полки со стороны корыта; 2 — галтель между полкой и профильной частью лопатки со стороны спинки; 3, 4, 7, 8 — зоны на бандажной полке; 5 — зона на профильной части лопатки; 6 — зона верхней впадины хвостовика лопатки Таблица 1 - Результаты расчетов
Наиболее повреждаемыми зонами данной лопатки являются: 1— галтель между рабочей и соседней гранями бандажной полки со стороны корыта лопатки; 2 — галтель между полкой и профильной частью лопатки со стороны спинки; 6 — верхняя впадина хвостовика лопатки. На рис. 5 приведены зависимости накопления повреждаемостей в этих зонах. При сравнении результатов расчетов и эксперимента установлено, что для зоны 1 прогнозируемая расчетная долговечность составляет 50 ч (рис. 6, а). После испытаний, проводимых в течение 45 ч, обнаружены трещины в галтели между рабочей и соседней гранями бандажной полки со стороны корыта лопатки на 12 рабочих лопатках, после 59 ч — на 20 лопатках (рис. 6, б). 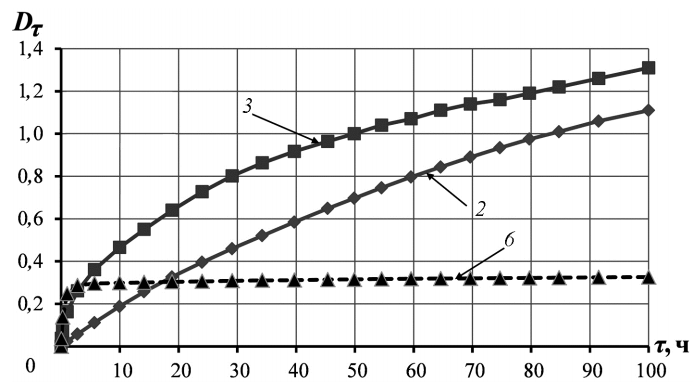 Рисунок 5 - Накопление повреждаемости с течением времени в зонах 1, 2 и 6  Рисунок 6 - Расчетные повреждаемости (а) и состояние лопатки после испытаний (б) Определенное расчетом напряженное состояние зоны 2 близко к предельному (повреждаемость 1 при 100 ч работы). После испытаний в течение 100 ч обнаружен значительный остаточный изгиб бандажных полок нескольких лопаток, что может предшествовать обрыву бандажной полки. Расчетные величины повреждаемости профильной части лопатки не превышают 0,27. В ходе испытаний дефектов на профиле рабочей лопатки не обнаружено. В зонах 4 и 7 (ребра бандажной полки) преобладают напряжения сжатия. Повреждаемости определены с учетом повышающего коэффициента 1,3. Поскольку в этих зонах лопатки дефектов не обнаружено, такая оценка считается достоверной. Зачастую ввиду отсутствия экспериментальных данных кинетику НДС при относительно низких температурах (< 800 °C) не рассчитывают, что может привести к занижению расчетной долговечности на несколько порядков. В данном примере учет кинетики НДС в зоне 6 (верхняя впадина хвостовика) при температурах 700 °C позволил уточнить запас по долговечности. Отношение долговечностей, определенных с учетом и без учета релаксации напряжений в этой зоне, составляет D**/D > 200. Трещин в хвостовике лопатки при испытании не обнаружено. На рис. 7 приведены изображения остаточных деформаций бандажной полки, определенные численно (а) и экспериментально (б).  Рисунок 7 - Расчетные значения остаточных деформаций бандажной Значения экспериментально установленных вытяжек по зонам 3 и 8 после 100 ч работы на рассмотренном режиме составляют 0,53 и 0,43 мм соответственно. Численно найденные значения деформаций — 0,55 и 0,42 мм. ЗаключениеЦелесообразность применения пользовательской модели ползучести подтверждают результаты, близкие к экспериментально определенным значениям, а также достаточно простая подготовка экспериментальных данных для расчета и возможность использовать ее в широком диапазоне значений напряжений, температур и продолжительности нагружения. В дальнейшем планируется разработать модель с учетом анизотропии свойств ползучести с целью достоверного прогнозирования кинетики НДС в трактовых и бандажных полках. Предложенный в данной работе способ расчета кинетики НДС позволяет адекватно определять расчетную долговечность и вытяжку деталей турбин как на этапе проектирования при использовании 2Dмоделей, так и на этапе поверочных 3D-расчетов. Список литературыКниги, монографии: Работнов Ю.Н. Ползучесть элементов конструкций. М.: Наука, 1966. 752 с. Васильев Б.Е., Магеррамова Л.А. Формирование уравнений ползучести сплавов для расчетов кинетики напряженно-деформированного состояния высокотемпературных лопаток турбин // Вестник Московского авиационного института. 2012. Т. 19, № 4. С. 99–107. Каблов Е.Н., Голубовский Е.Р. Жаропрочность никелевых сплавов. М: Машиностроение, 1998. 464 с. Бессчетнов В.А., Дильман М.А., Березин Р.И. Оценка статической прочности лопаток ТВД по результатам расчета напряженнодеформированного состояния в 3D-постановке с учетом ползучести материала [Электронный ресурс] // Авиадвигатели XXI века: материалы конф. Электрон. дан. М.: ЦИАМ, 2010 Биргер И.А., Шорр Б.Ф., Иосилевич Г.Б. Термопрочность деталей машин. М.: Машиностроение, 1975. 455 с. Электронные ресурсы: Imaoka S. User creep subroutine // ANSYS Tips website. URL.: http:// ansys.net/collection/1061, 2007. ANSYS Structural analysis guide // ANSYS DOCUMENTATION. |