1 Информация. Понятие информации. Концепции информации
 Скачать 0.93 Mb. Скачать 0.93 Mb.
|
13 Системы счисления (основание, полином, понятие разряда, длина числа)Система счисления - совокупность приемов и правил изображения чисел цифровыми знаками Системы счисления делятся на непозиционные и позиционные. Непозиционная система счисления - система, в которой значение символа не зависит от его положения в числе. Позиционнаясистема счисления -система, в которой значение символа зависит от его места в ряду цифр, изображающих число. О 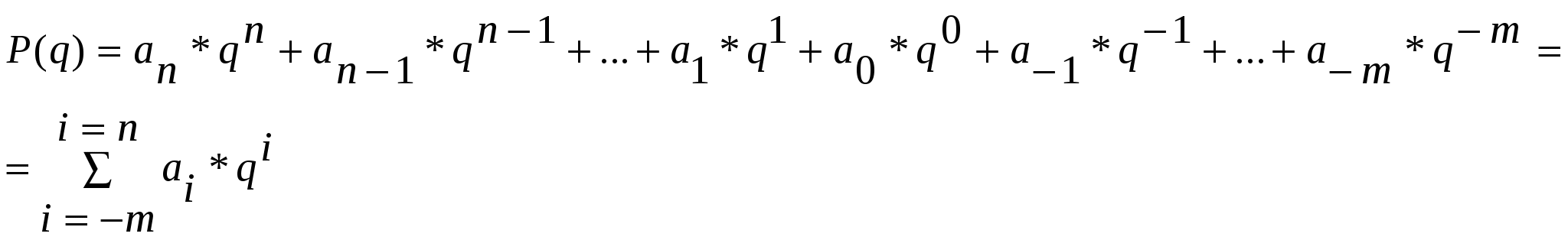 снование (базис) позиционной системы счисления - количество знаков или символов, используемых в разрядах для изображения числа в данной системе счисления.(q) Для позиционной системы счисления с общим основанием справедливо равенство где q - основание позиционной системы счисления; P(q) - произвольное число; an - коэффициент ряда( цифры системы счисления); n,m - количество целых и дробных разрядов. Возможно множество позиционных систем, так как за основание можно принять любое целое число. Вес разряда pi числа в позиционной системе счисления есть отношение вида pi = qi/q0 (1) i - номер разряда справа налево pi = q i / q 0 = q i , где I - номер разряда справа налево. Если разряд имеет вес pi= q i, то следующий старший разряд будет иметь вес p i+1 = q i+1 , а предыдущий младший разряд-вес p i-1 = q i-1 ,. таким образом, в позиционной системе счисления вес разряда определяется его положением (позицией) в числе. Такая взаимосвязь разрядов приводит к необходимости передачи информации между ними. Если при сложении в данном разряде накопилось значение, равное или большее q - основания системы счисления, то должна происходить передача единицы в соседний старший разряд с уменьшением его на q, т. е. передача единицы переноса. Если при вычитании в данном разряде число единиц оказалось меньше нуля, то должна происходить передача единицы займа из соседнего старшего разряда с увеличением его на q для данного разряда. Передача переносов или займов происходит последовательно от разряда к разряду. Длина числа - количество разрядов (позиций) в записи числа. 001101011- 9 разрядов (2) 235961 - 6 разрядов Длина разрядной сетки -( n ) термин, используемый для определения длины числа. В разных системах счисления длина разрядной сетки при записи одного и того же числа неодинаковая. Диапазон представления (ДП) чисел в заданной системе счисления - интервал числовой оси, заключенный между максимальными и минимальными числами, представленными длиной разрядной сетки. 14 Перевод чисел из одной системы счисления в другуюЧисло N делим на новое основание q . Полученный от деления первый остаток является младшей цифрой целой части числа в системе с основанием q . Целую часть полученного числа снова делим на основание q . В результате определим второй остаток, равный следующей после младшей цифре числа в системе с основанием q . Деление проводим до тех пор, пока не получим частное, меньшее делителя. Последнее частное дает старшую цифру числа в системе с основанием q Действия производим в той системе счисления, из которой переводим. Случай 0 < N <1 Умножаем Np на q и берем a -1 , равной целой части результата умножения Np на q , умножаем полученнуюдробную часть на q и берем в качестве a -2 целую часть результата и т.д. Действия производим в системе счисления с основанием р, т.е. в той системе счисления, из которой переводим. Примеры: 0,29 10 --- > N 2 0,29 10 = 0,0100102
Этот процесс не обязательно будет конечным, как для целых чисел . Он может продолжаться до любого числа значащих цифр. Число цифр в числе, представленном в системе счисления с основанием q , определяет точность; обычно точность числа в новой системе берется в соответствии с точностью числа в системе счисления с основанием р. Случай перевода нецелых чисел, больших 1. Перевод чисел, имеющих целую и дробную части, выполняется в два этапа: вначале переводится целая часть, а затем - дробная. |
