Дифзачет. дифзачет. 1. История развития понятия числа. Действительные числа
 Скачать 1.26 Mb. Скачать 1.26 Mb.
|
|
Вопросы к дифференцированному зачету по математике за 1 семестр 1. История развития понятия числа. Действительные числа Число – это основное понятие математики, используемое для количественной характеристики сравнения и нумерации. Натуральные числа – числа, начиная с единицы, используемые при счете предметов. 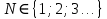 Целые числа –это все натуральные числа, а так же все числа противоположные им по знаку и число 0. Z 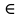 {0;±1;±2;±3…} {0;±1;±2;±3…}Рациональные числа – 1) числа, которые можно представить в виде дроби 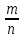 , , 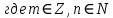 . 2) множество бесконечных периодических, десятичных дробей.(Q) . 2) множество бесконечных периодических, десятичных дробей.(Q)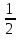 =0.5 – конечная дробь =0.5 – конечная дробь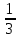 =0.333=0.(3) – бесконечная десятичная периодическая дробь =0.333=0.(3) – бесконечная десятичная периодическая дробь Иррациональные числа – 1) это числа, не представимые в виде обыкновенной дроби. 2) множество бесконечных десятичных непериодических дробей. (I) 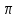 =3.14159… =3.14159… е=2.71828… (число Эйлера) 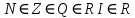 Действительные числа – 1) это любые рациональные и иррациональные числа 2) бесконечные (периодические и непериодические) десятичные дроби. R=Q  2. Десятичные приближения действительных чисел. Пусть 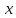 – точное значение, – точное значение,  – его приближенное значение. – его приближенное значение.Абсолютная погрешность приближенного значения ( 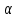 ) – модуль разности между точным числом x и его приближенным значением a. ) – модуль разности между точным числом x и его приближенным значением a.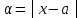 Число a называется приближенным значением точного числа x с точностью до 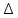 a, если абсолютная погрешность приближенного значения a не привышает a, если абсолютная погрешность приближенного значения a не привышает 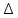 a. a.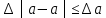 Число 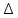 a – граница абсолютной погрешности приближенного числа а. a – граница абсолютной погрешности приближенного числа а.3,6 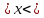 3,7 3,7а= 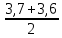 = 3,65 = 3,65доверительный интервал 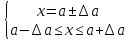 Цифра m приближенного числа а называется верной в широком смысле, если граница абсолютной погрешности числа а не превосходит единицы того разряда, в котором записывается цифра m. Цифра m приближенного числа а называется верной в строгом (узком) смысле, если граница абсолютной погрешности числа а не превосходит половины единицы того разряда, в котором записана цифра m. Сомнительные цифры −цифрыв записи приближенного числа, о которых неизвестно являются ли они верными. Значащие цифры приближенного числа– все его верные цифры кроме 0, стоящих перед первой цифрой (слева направо) отличной от 0. Абсолютная величина разности │а - 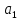 │− погрешность округления. │− погрешность округления.Относительная погрешность 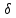 приближенного значения а числа х – отношение абсолютной погрешности приближенного значения а числа х – отношение абсолютной погрешности 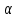 этого приближения к модулю числа а. этого приближения к модулю числа а.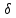 = =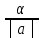 Граница относительной погрешности 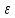 приближенного значения а – отношение границы абсолютной погрешности приближенного значения а – отношение границы абсолютной погрешности 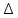 а к модулю числа а. а к модулю числа а.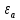 = =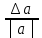 или или 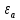 = =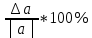
3. Корни натуральной степени из числа и их свойства. 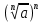 =a =a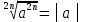 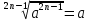 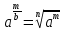 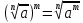  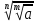 = =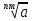 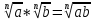 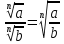 4. Степень с рациональным и действительными показателями, их свойства 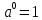 a a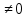 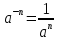 n n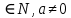 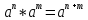 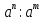 = =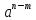 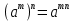 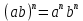 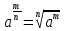  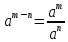 5. Логарифмы и их свойства. Основное логарифмическое тождество. Логарифм числа b по основанию а – это показатель степени, в которую нужно возвести основание а, чтобы получить b. 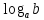 b 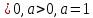 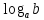 =c =c 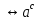 =b =bДесятичный логарифм – логарифм по основанию по основанию 10. lgb=  Натуральный логарифм – логарифм по основанию е.  = =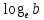 е ≈ 2,7 Основное логарифмическое тождество. 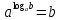 Свойства логарифмов 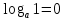 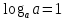 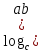 ) = ) =  = =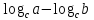 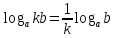 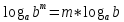 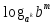 = =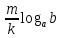 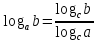  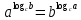 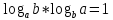 6. Логарифмирование и потенцирование выражений. Логарифмирование – это преобразование, при котором логарифм выражения с переменными приводится к сумме или разности логарифмов переменных. Потенцирование – нахождение числа по известному логарифму. 7. Формула перехода от одного основания логарифма к другому. 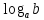 = =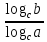 8. Числовая функция. График функции. Зависимость переменной y от переменной x называется функцией, если каждому значению x отвечает только одно значениеy. Переменную x называют независимой переменной или аргументом, a переменную y– зависимой переменной. Значение y, которое отвечает данному значению x, называют значением функции f в точке a и обозначают символом f(x) 9. Простейшие преобразования графиков функции.
10. Свойства функции: монотонность, ограниченность, чётность и нечётность, периодичность. Функция 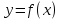 называется возрастающей на множестве Х, если для любых называется возрастающей на множестве Х, если для любых 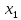 и и 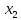 из X при из X при 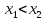 , выполняется неравенство f( , выполняется неравенство f( , то есть если меньшему значению аргумента в этом множестве соответствует меньшее значение функции. , то есть если меньшему значению аргумента в этом множестве соответствует меньшее значение функции. Функция 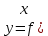 ) называется убывающей на множестве Х, если для любых ) называется убывающей на множестве Х, если для любых 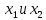 из X при из X при 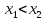 выполняется неравенство выполняется неравенство 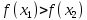 . .Функцию 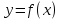 называется ограниченной снизу/сверху на множестве Х, если все значения функции на множестве Х больше/меньше некоторого числа. называется ограниченной снизу/сверху на множестве Х, если все значения функции на множестве Х больше/меньше некоторого числа.Функция 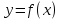 называется четной, если область её определения симметрична относительно оси ординат и выполняется равенство называется четной, если область её определения симметрична относительно оси ординат и выполняется равенство 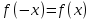 . .Функция 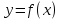 называется нечетной, если область её определения симметрична относительно начала координат и выполняется равенство называется нечетной, если область её определения симметрична относительно начала координат и выполняется равенство 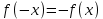 . .Функция 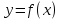 называется периодической с периодом называется периодической с периодом 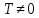 , если для любого , если для любого 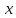 в области определения функции в области определения функции 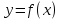 выполняется равенство выполняется равенство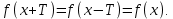 |

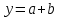

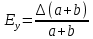
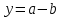
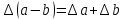

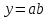
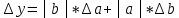
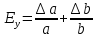
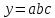
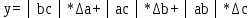
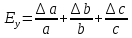
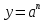
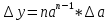


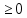 и отобразить график функции y=f(x) для y
и отобразить график функции y=f(x) для y +bx+c,
+bx+c,
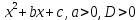
 или сжать к оси абсцисс в а раз (
или сжать к оси абсцисс в а раз (
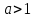 ) или растянуть от оси ординат в а раз (
) или растянуть от оси ординат в а раз (