Дифзачет. дифзачет. 1. История развития понятия числа. Действительные числа
 Скачать 1.26 Mb. Скачать 1.26 Mb.
|
|
11. Обратные функции. График обратной функции. 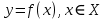 является обратной, если любое своё значение она имеет только в одной точке множества является обратной, если любое своё значение она имеет только в одной точке множества 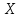 (когда разным значением аргумента соответствуют разные значения функции). (когда разным значением аргумента соответствуют разные значения функции).Т.1. Если функция 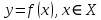 монотонна на множестве монотонна на множестве 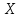 , то она обратима. , то она обратима.Т.2. Если функция 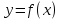 возрастает на множестве возрастает на множестве 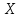 и область значений функции есть множество и область значений функции есть множество 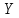 , то обратная функция , то обратная функция 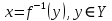 возрастает на множестве Y или если функция возрастает на множестве Y или если функция 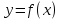 убывает на множестве убывает на множестве 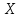 и область значений функции есть множество Y, то обратная функция и область значений функции есть множество Y, то обратная функция 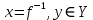 убывает на множестве Y. убывает на множестве Y.Т.3. Точки 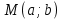 функции функции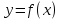 и и 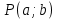 функции функции 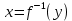 симметричны относительно прямой симметричны относительно прямой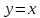 12.Степенная функция, её графики и свойства. Степенная функция – функция 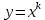 , где , где 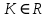 . . 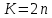 – четное натуральное число. – четное натуральное число.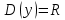 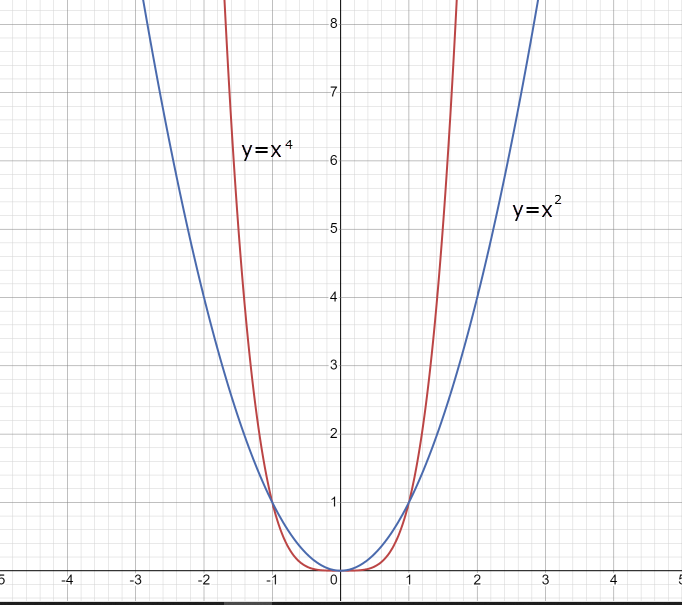 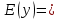 Функция четная а) 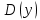 – симметричное множество – симметричное множествоб) 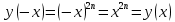 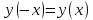 функция четная функция четнаяФункция убывает при 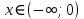 Функция возрастает при 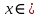 Функция непрерывная Непериодическая функция 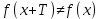 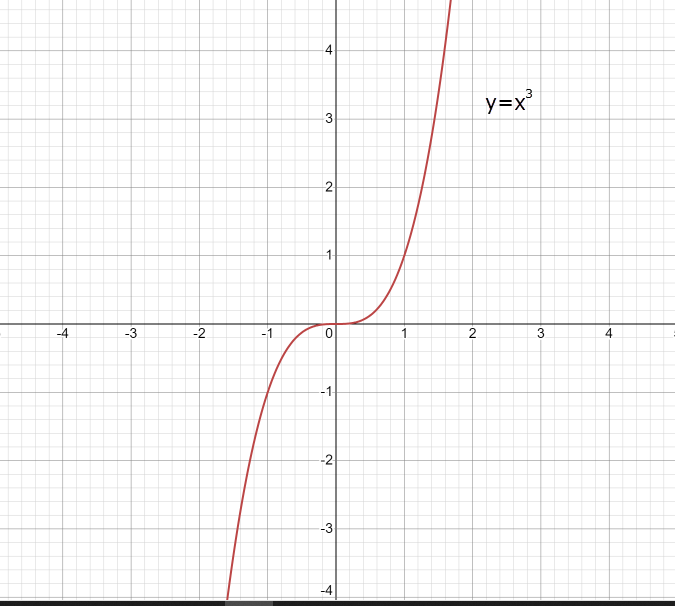 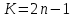  нечетное натуральное число нечетное натуральное число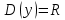 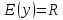 Функция нечетная а) 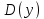 – симметричное множество – симметричное множествоб) 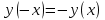 – нечетная функция – нечетная функция4. Функция возрастает на 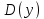 5. Функция непрерывная 6. Непериодическая функция 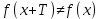 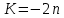 , где n − натуральное число , где n − натуральное число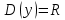 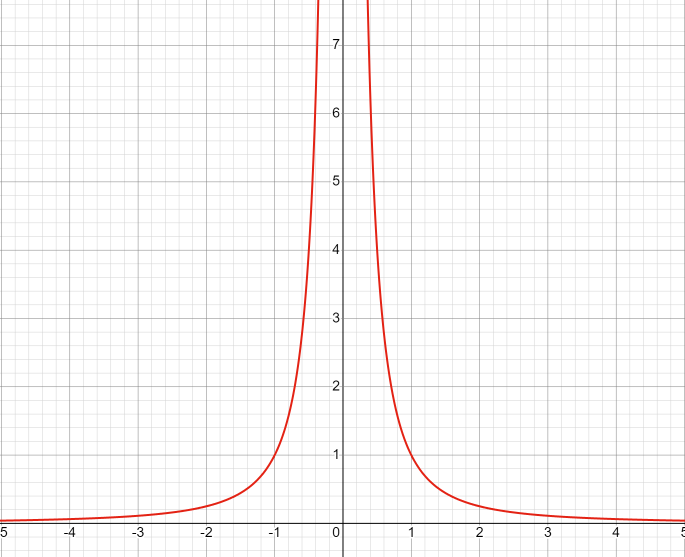 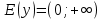 Функция четная а) 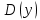 – симметричное множество – симметричное множествоб) 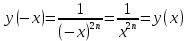 Функция возрастает при 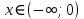 Функция убывает при 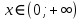 Функция непрерывная Функция непериодическая 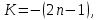 где где 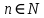 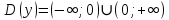 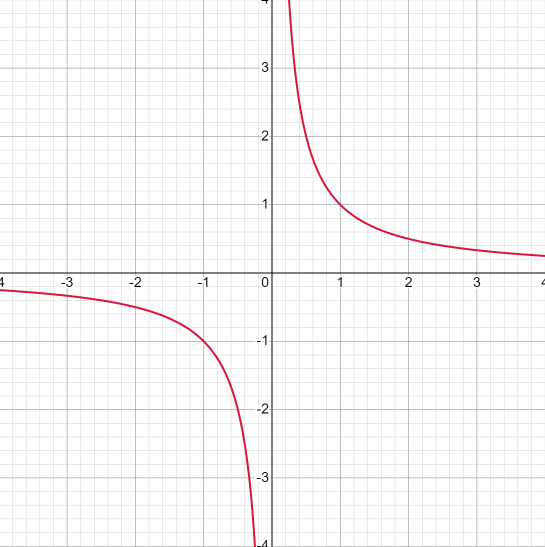 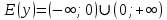 Функция нечетная а) 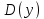 – симметричное множество – симметричное множествоб) 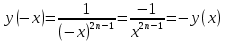 Функция убывает при 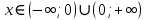 Функция непрерывная 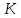 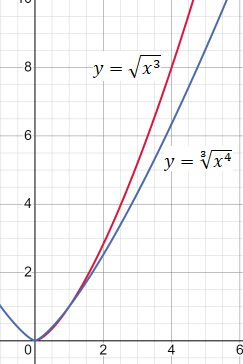 – положительное действительное нецелое число – положительное действительное нецелое число 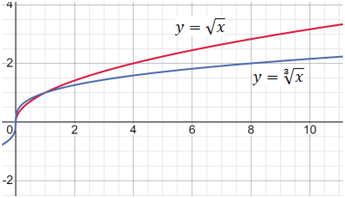 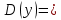 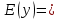 Функция не четная, не нечетная. Функция общего вида. Множество 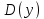 несимметрично несимметричноФункция возрастает при 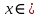 Функция непрерывная на 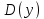 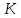 – отрицательное действительное нецелое – отрицательное действительное нецелое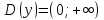 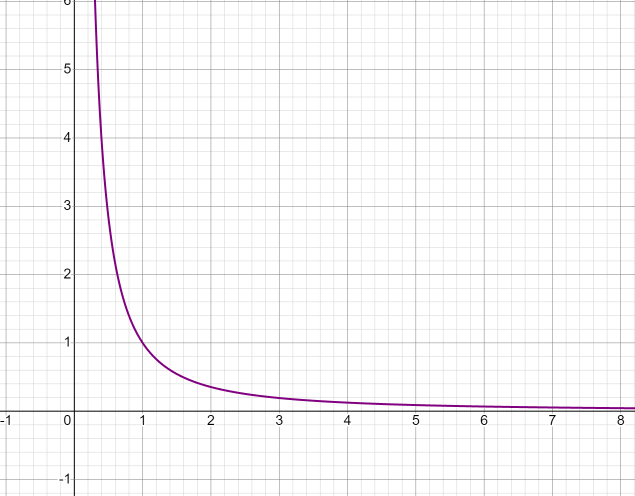 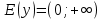 Функция убывающая при 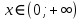 Функция общего вида, не является четной и нечетной Функция непрерывная на 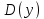 13. Показательная функция, её графики и свойства. Функция вида 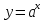 , где основанием служит заданное число , где основанием служит заданное число 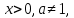 называется показательной функцией. называется показательной функцией.
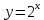 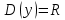 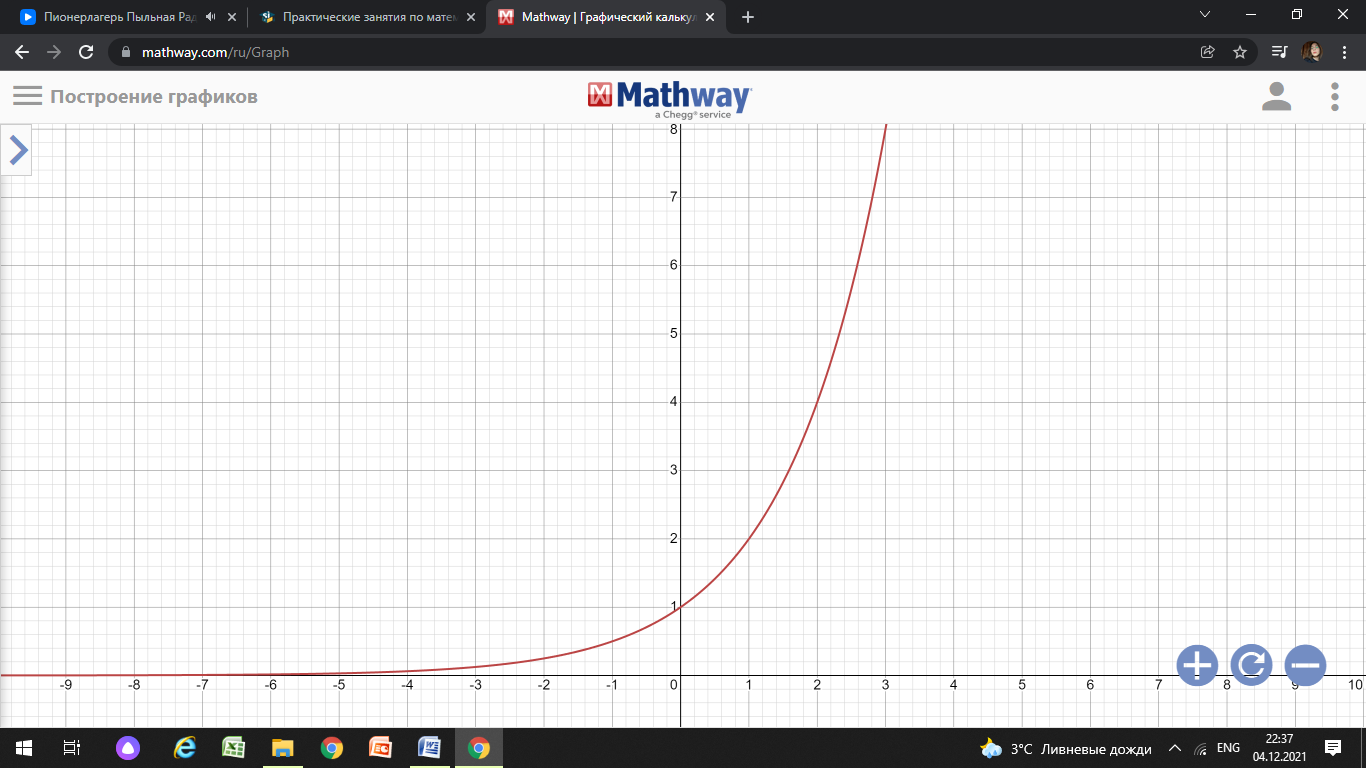 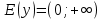 Функция возрастает при 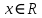 , если , если 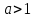 Функция общего вида а) 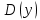 – симметричное множество – симметричное множествоб) 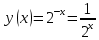 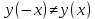 − не является четной − не является четной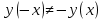 – не является нечетной – не является нечетной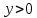 при при 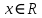 Точки пересечения с осью 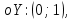 с осью с осью 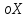 не пересекается не пересекаетсяФункция непрерывная Функция непериодическая
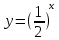 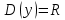 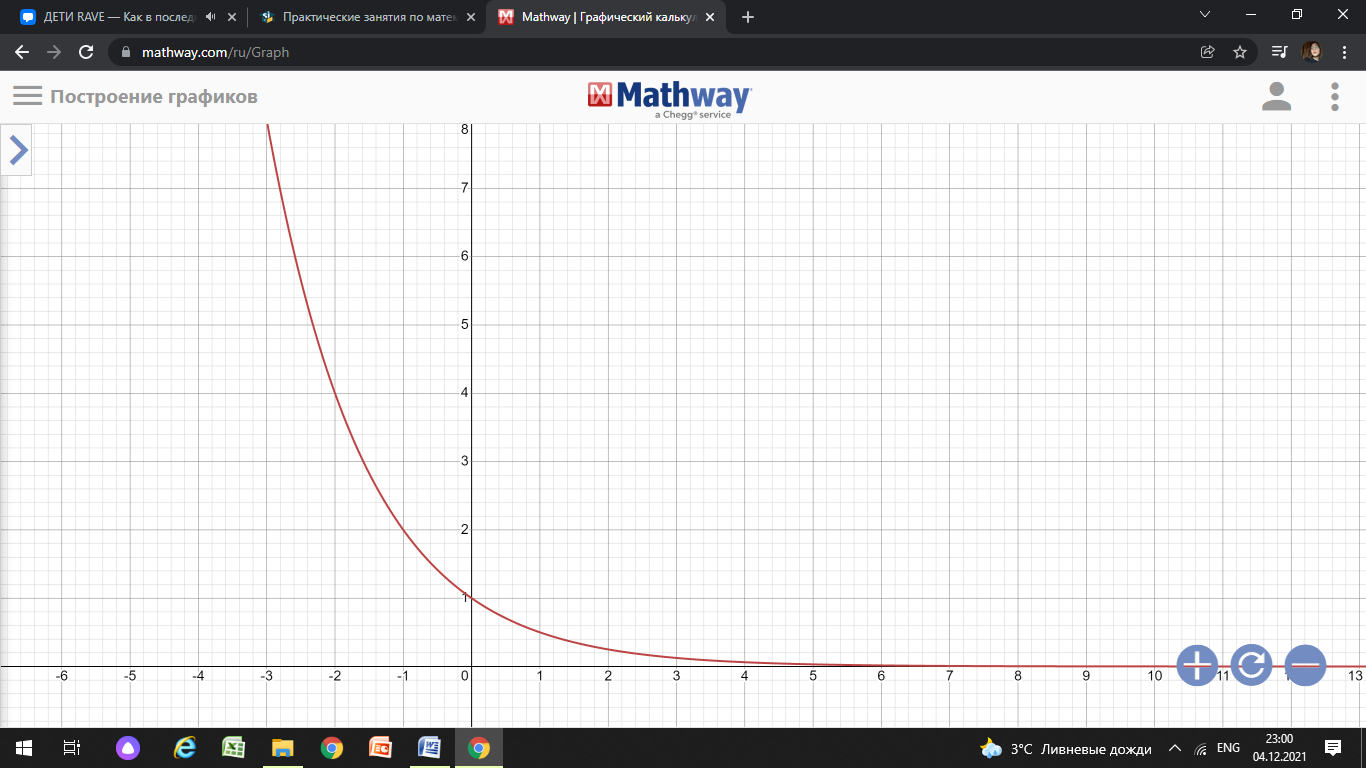 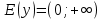 Функция убывает при 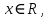 если если 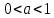 Функция общего вида а) 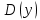 – симметричное множество – симметричное множествоб) 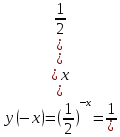 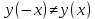 – не является четной – не является четной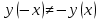 – не является нечетной – не является нечетной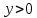 при при 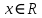 Точки пересечений с осью 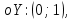 с осью с осью 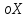 не пересекается не пересекаетсяФункция непрерывная Функция непериодическая 14. Показательные уравнения. Уравнения, содержащее переменную в показателе степени, называются показательными. При решении показательных уравнений вида 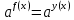 (где (где 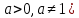 используем свойство используем свойство 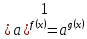 2) 2)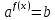 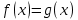 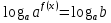 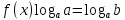 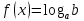 15. Показательные неравенства. Неравенства вида 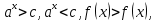 где где 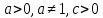 называются простейшими показательными неравенствами. называются простейшими показательными неравенствами.Имеют место следующие равносильные преобразования: 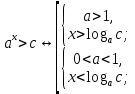 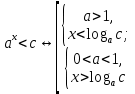 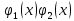 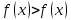 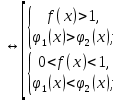 16. Логарифмическая функция, её графики и свойства. Логарифмической называется функция вида 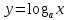 , где , где 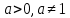 1 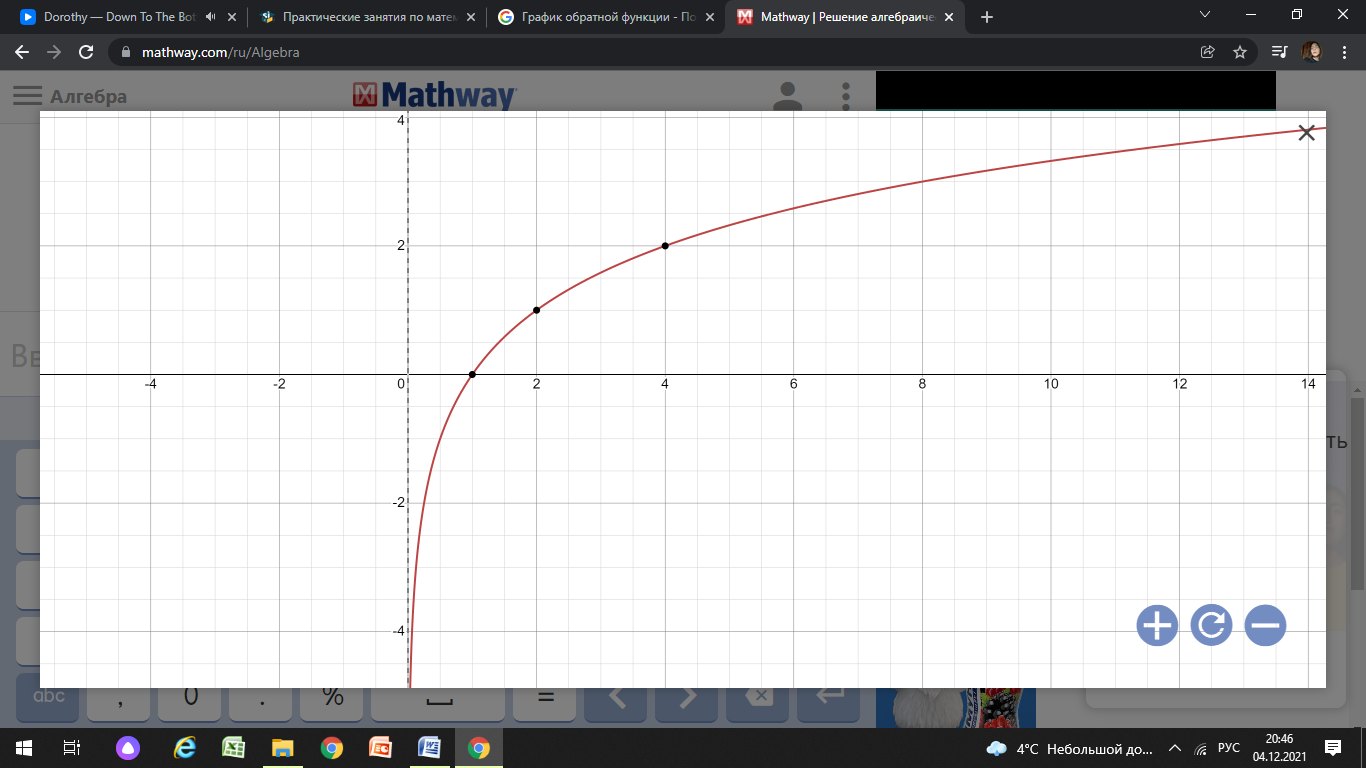 ) )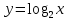 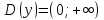 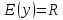 Функция возрастает при 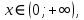 если если 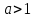 Функция общего вида. 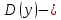 несимметричное множество несимметричное множество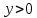 при при 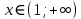 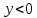 при при 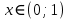 Точки пересечения с осью 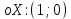 , с осью , с осью 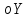 не пересекаются не пересекаютсяФункция непрерывная для 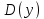 Функция непереиодическая 2 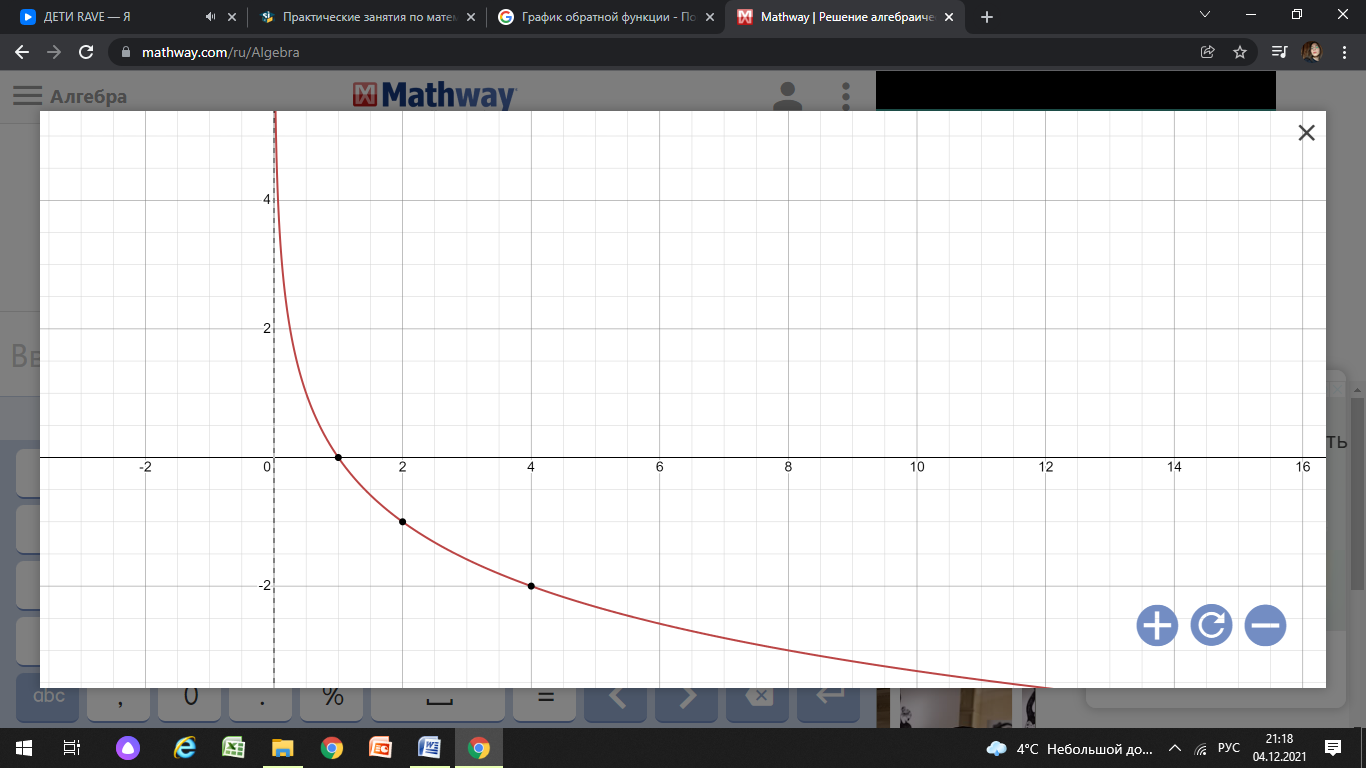 ) ) 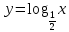 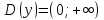 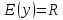 Функция убывает при 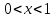 или или 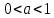 Функция общего вида. 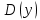 – несимметричное множество – несимметричное множество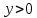 при при 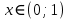 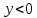 при при 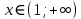 Точки пересечения с осью 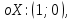 с осью с осью 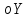 не пересекается не пересекается Функция непрерывная на 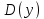 Функция непериодическая 17. Логарифмические уравнения. Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим. 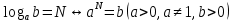 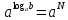 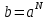 18. Логарифмические неравенства. Неравенства вида 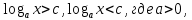 называются простейшими логарифмическими неравенствами. называются простейшими логарифмическими неравенствами.Имеют место следующие преобразования: 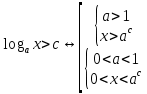 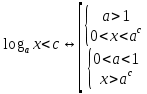 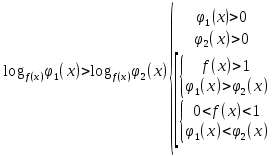 19. Радианная мера угла. Радианная мера угла  – отношение длины дуги окружности – отношение длины дуги окружности 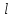 к длине радиуса к длине радиуса 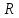 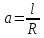 |

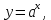 где
где