Дифзачет. дифзачет. 1. История развития понятия числа. Действительные числа
 Скачать 1.26 Mb. Скачать 1.26 Mb.
|
|
20. Синус, косинус, тангенс и котангенса числа. Абсцисса 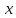 точки точки 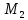 числовой единичной окружности называется косинусом числа числовой единичной окружности называется косинусом числа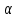 : : 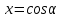 Ордината 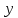 точки точки 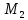 числовой единичной окружности называется синусом числа числовой единичной окружности называется синусом числа 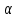 : :  Отношение синуса числа 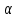 к его косинусу называется тангенсом числа к его косинусу называется тангенсом числа 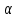 : :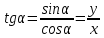 Отношение косинуса числа 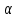 к его синусу называется котангенсом числа к его синусу называется котангенсом числа 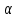 : :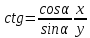 21. Знаки и числовые значения синуса, косинуса, тангенса и котангенса числа. 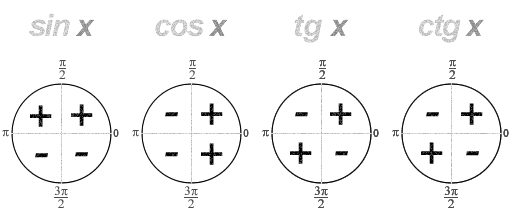 22. Соотношения между тригонометрическими функциями одного аргумента. 1. 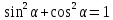 2. 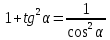 3. 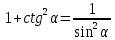 4. 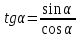 5. 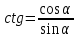 6. 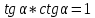 2 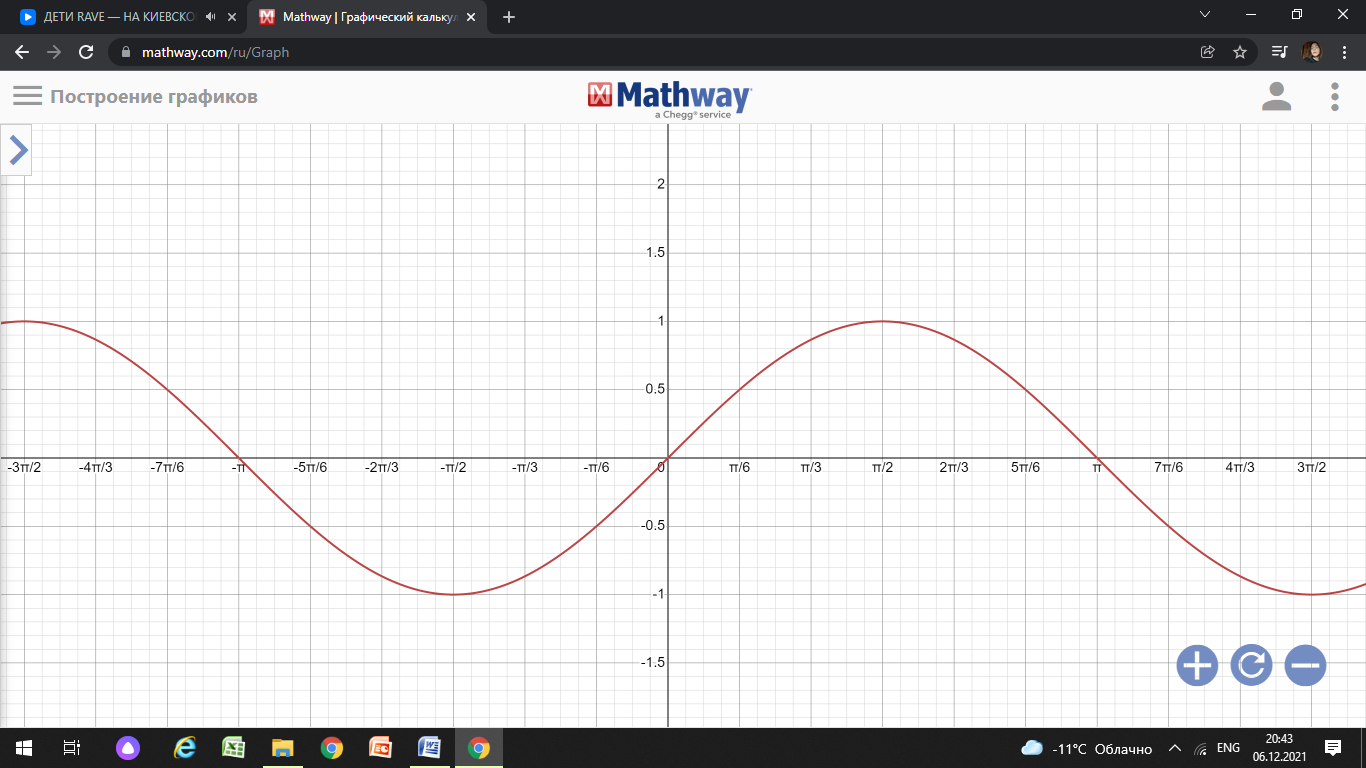 3. Тригонометрическая функция y=sinx. График и свойства. 3. Тригонометрическая функция y=sinx. График и свойства.1. 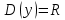 2. 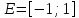 3. Нечетная 4.Наименьший положительный период: 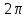 5. Координаты точек пересечения с осью а) 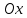 – – 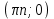 б) 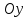 – – 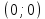 6. Промежутки, на которых функция принимает: а) положительные значения: 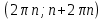 б) отрицательные значения: 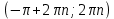 7. Промежутки а) возрастания: 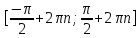 б) убывания:  8. Точка минимума: 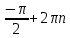 . Точка максимума: . Точка максимума: 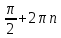 9. Минимум функции: 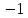 . Максимум функции: . Максимум функции: 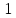 24. Тригонометрическая функция y=cosx. График и свойства. 1 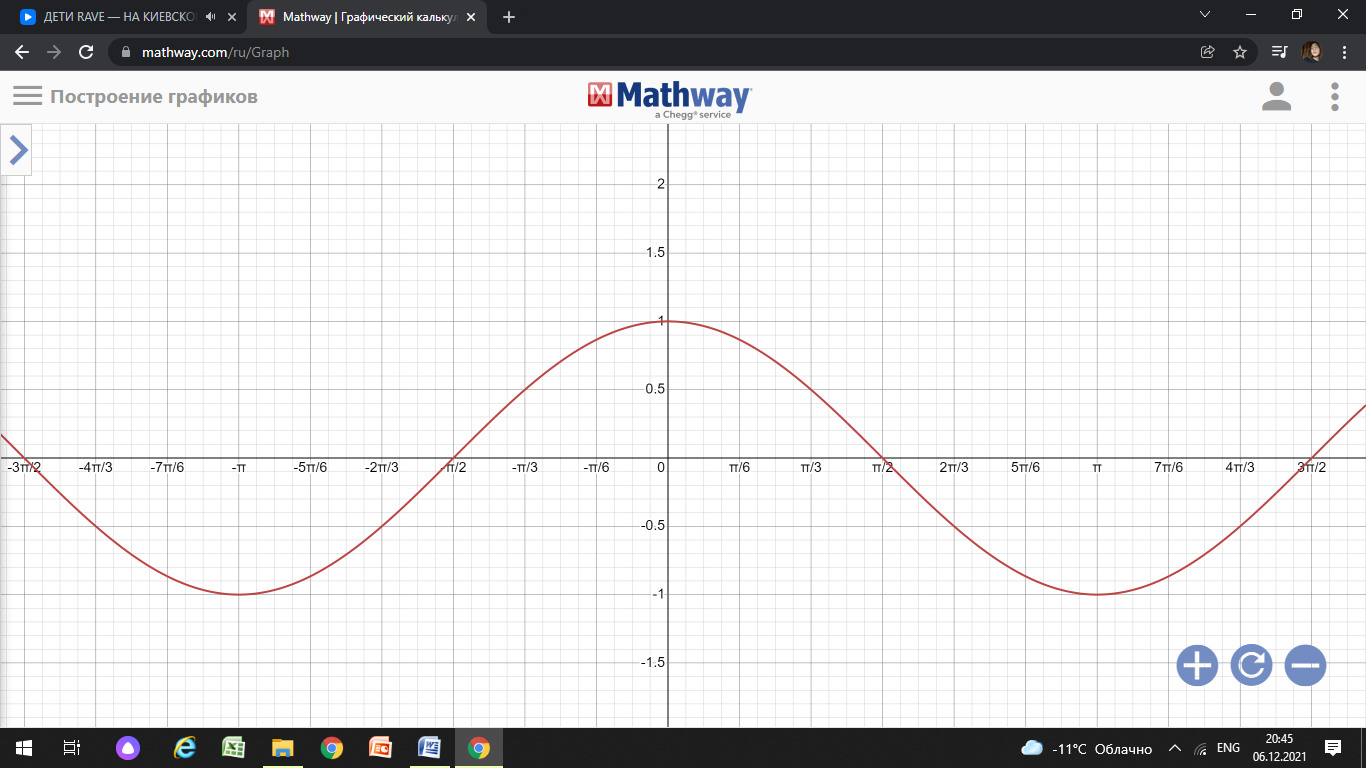 . . 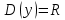 2. 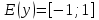 3. Четная 4. Наименьший положительный период: 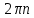 5. Координаты точек пересечения графика функции с осью: а) 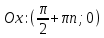 б) 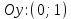 6. Промежутки, на которых функция принимает: а) положительные значения: 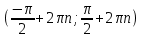 б) отрицательные значения: 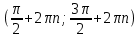 7. Промежутки: а) возрастания: 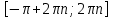 б) убывания:  8. Точка минимума: 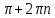 . Точка максимума . Точка максимума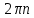 9. Минимум функции: 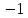 . Максимум функции: . Максимум функции: 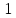 25. Тригонометрическая функция y=tgx. График и свойства. 1 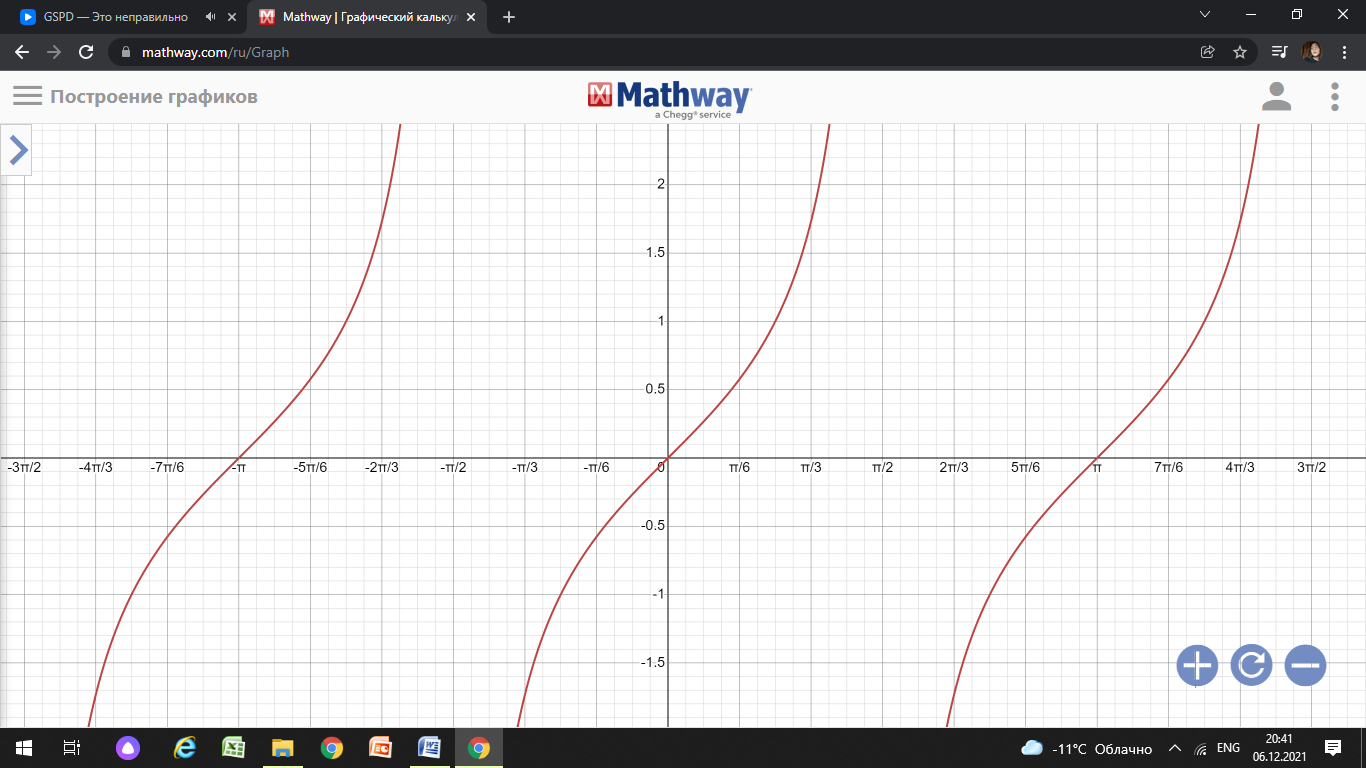 . . 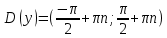 2. 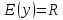 3. Нечетная 4. Наименьший положительный период: 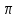 5. Координаты точек пересечения графика функции с осью: а) 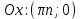 б) б) 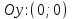 6. Промежутки, на которых функция принимает а) положительные значения: 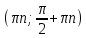 б) отрицательные значения: 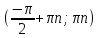 7. Экстремумы отсутствуют 8. Функция возрастает на каждом интервале области определения 9. Асимптота: 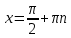 26. Тригонометрическая функция y=ctgx. График и свойства. 1 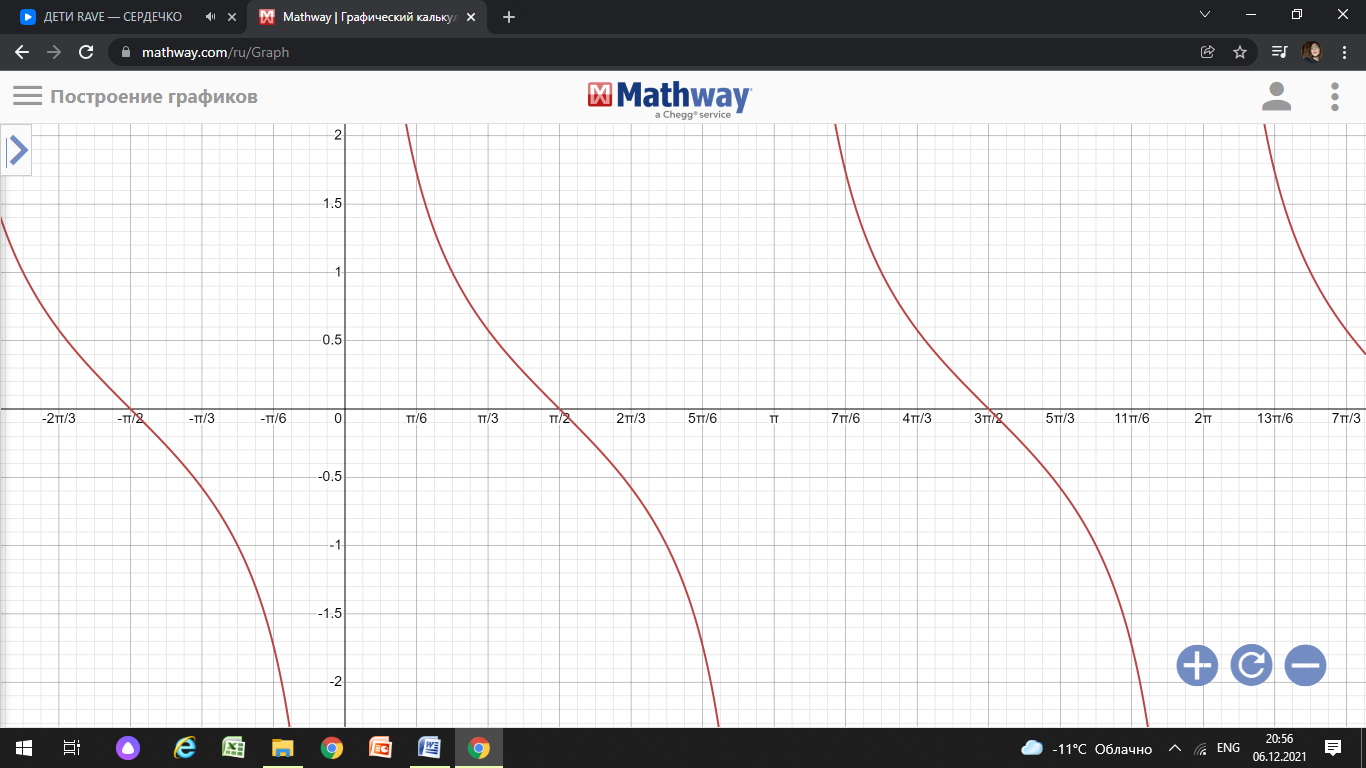 . . 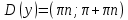 2. 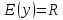 3. Нечетная 4. Наименьший положительный период: 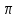 5. Координаты точек пересечения графика функции с осью а) 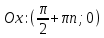 б) 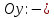 6. Промежутки, на которых функция принимает а) положительные значения: 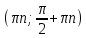 б) отрицательные значения: 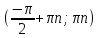 7. Экстремумы отсутствуют 8. Функция убывает на каждом интервале области определения 9. Асимптота:  27. Арксинус, арккосинус, арктангенс, арккотангенс числа. 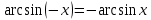 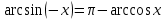 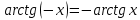 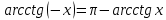 28. Простейшие тригонометрические уравнения. Простейшими тригонометрическими уравнениями называются уравнения вида, где sinx=m, cosx=m, tgx=m, ctgx=m, где m – это число. 29. Простейшие тригонометрические неравенства. Неравенства sin x>m, sin x Решить простейшее тригонометрическое неравенство, значит найти множество всех значений аргумента которые обладают данные неравенства в верное числовое неравенство. 30. Формулы приведения. Формул приведения позволяют выразить тригонометрическая функции углов 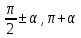 , 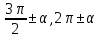 через тригонометрические функции угла α. через тригонометрические функции угла α.При применении формул приведения рекомендуется пользоваться следующими правилами: 1.Если α откладывается от оси OX, то наименование приводимой функции, т.е. функции аргумента –α,π±α,2π±α, изменяется. Если же α откладывается от оси OY, от наименование приводимой функции, т.е. функции аргумента 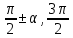 ±α заменяются на сходное (синус – на косинус, тангенс – на котангенс и наоборот). ±α заменяются на сходное (синус – на косинус, тангенс – на котангенс и наоборот).2. Знак, с которым нужно брать тригонометрическую функцию в правой части находится по знаку левой части в предположении, что 0<α< 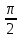 . .31. Тригонометрические функции суммы и разности двух аргументов. Sin(α+β)=sinα cosβ + cosα sinβ Sin(α-β)=sinα cosβ - cosα sinβ Cos(α+β)=cosα cosβ – sinα sinβ Cos(α-β)=cosα cosβ + sinα sinβ Tg(α+β)= 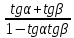 32. Тригонометрические функции удвоенного и половинного аргументов. Sin2α=2sinαcosα Cos2α= 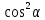 - -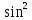 α αTg2α= 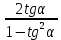 Ctg2α= 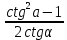 Tg(α-β)= 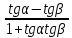 Ctg(α+β)= 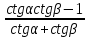 Ctg(α-β)= 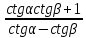 33. Преобразование произведения тригонометрических функций в алгебраическую сумму. Sinαcosβ= 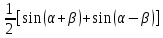 Cosαcosβ= 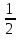 [cos(α+β)+cos(α-β)] [cos(α+β)+cos(α-β)]Sinαsinβ= 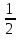 [cos(α-β)-cos(α+β)] [cos(α-β)-cos(α+β)]34. Преобразование суммы и разности двух одноимённых тригонометрических функций в произведение. Sinα+sinβ=2sin 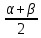 cos cos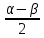 Sinα-sinβ=2cos 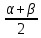 sin sin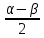 Cosα+cosβ=2cos 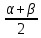 cos cos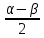 Cosα-cosβ=2sin 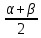 sin sin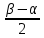 Tgα+tgβ= 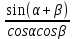 Tgα-tgβ= 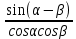 |
