гвв. 1 Классификация и физический механизм работы вч и свч генераторов
 Скачать 5.65 Mb. Скачать 5.65 Mb.
|
Общие сведения об угловой модуляции⇐ Предыдущая38394041424344454647Следующая ⇒
u(t)=Ucos(ωt+φ)= UcosФ(t) (9.1) Очевидно, что в соответствии с передаваемой информацией, помимо амплитуды, можно менять частоту ω или фазу φ, осуществляя, таким образом, частотную или фазовую модуляцию (ЧМ, ФМ). Согласно (9.1) в обоих случаях будет меняться угловой аргумент косинуса Ф(t), поэтому частотную и фазовую модуляцию объединяют общим термином «угловая модуляция». Тем не менее, как будет показано ниже, между ЧМ и ФМ есть и существенные различия. Воспользуемся простейшей моделью информационного сигнала в форме (7.1). Тогда колебание с частотной модуляцией можно представить в следующем виде u(t)=Ucos[(ω+ΔωcosΩt)t+φо] (9.2) В этом выражении Δω – амплитуда отклонения частоты при ЧМ, получившая название – девиация частоты; φо – произвольная постоянная, соответствующая фазовому сдвигу при t = 0. Согласно (7.1) и (9.1) Δω=Кчм·UΩ (9.3) Здесь Кчм - крутизна характеристики частотного модулятора. Аналогично для фазовой модуляции получим u(t)=Ucos(ωt+ΨcosΩt+φο) (9.4) В этом выражении Ψ – амплитуда отклонения фазы, названная индексом модуляции. По аналогии с (9.3) Ψ=Кфм·UΩ (9.5) Где Кфм - крутизна характеристики фазового модулятора. Частота и фаза гармонического колебания связаны следующими соотношениями Используя эти зависимости можно определить связь между ЧМ и ФМ. Подставив значение Ф(t) из (9.4) в (9.6), определим как изменяется частота при ФМ Сравнивая частоту в выражениях (9.2) и (9.8), с учётом (9.5), получим Δω(ФМ) = ΨΩ = Ω·Кфм·UΩ (9.9) Таким образом, девиация частоты при ФМ пропорциональна амплитуде информационного сигнала и его частоте, в отличие от (9.3). Поэтому, в информационном сигнале, переданном фазовой модуляцией и принятым частотным детектором, произойдёт подъём верхних частот (исказится амплитудно-частотная характеристика). Подставим теперь частоту из (9.2) в (9.7) и определим как меняется фаза при ЧМ . Сравнивая фазу в (9.4) с (9.10), с учётом (9.3), получим В этом случае, индекс модуляции при ЧМ пропорционален амплитуде информационного сигнала и обратно пропорционален его частоте, в отличие от (9.5). Поэтому, в информационном сигнале, переданном частотной модуляцией и принятом фазовым детектором, произойдёт завал верхних частот. Рассмотренные отличия проявляются только в случае реальных информационных сигналов с меняющейся частотой Ω. Для его модели (7.1) с постоянной частотой, различие между ЧМ и ФМ полностью отсутствует. На основании (9.9) и (9.11) возможно взаимное преобразование ЧМ в ФМ и наоборот, обеспечив необходимую зависимость (или независимость) индекса модуляции от частоты модулирующего сигнала. В частности, для преобразования ФМ в ЧМ, необходимо амплитуду модулирующего сигнала изменять обратно пропорционально его частоте. Это может быть выполнено с помощью интегрирующей RC цепи, через которую перед модуляцией должен быть пропущен модулирующий сигнал (см. рисунок 9.1а). 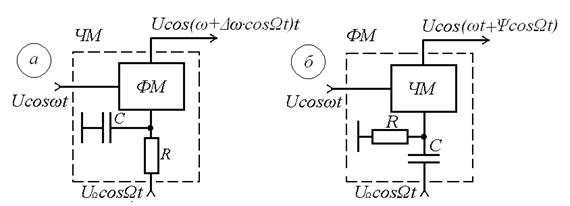 Рисунок 9.1 – Преобразование видов угловой модуляции Действительно, коэффициент передачи такой цепи 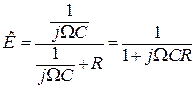 . При условии R>>ΩмаксС . При условии R>>ΩмаксС(9.12) Аналогично при использовании дифференцирующей цепи на входе частотного модулятора можно получить фазовую модуляцию (см. рисунок 9.1б). |
