Шпоры(Процессы и аппараты). 1. Классификация основных процессов

• Название: 1. Классификация основных процессов
• Анкор: Шпоры(Процессы и аппараты).docx
• Дата: 18.05.2017
• Размер: 428.64 Kb.
• Имя файла: Шпоры(Процессы и аппараты).docx
• Тип: Документы; #7827
• страница: 3 из 3

18. Дифференциальные уравнения движения Навье—Стокса

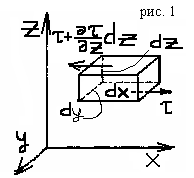
При движении реальной (вязкой) жидкости в потоке жидкости помимо сил давления и тяжести действуют также силы трения. Действие сил трения Т на выделенный в потоке вязкой жидкости элементарный параллелепипед (рис. 1) проявляется в возникновении на его поверхности касательных напряжений τ. Рассмотрим первоначально относительно простой случай одномерного плоского потока капельной жидкости в направлении оси x когда проекция скорости ω_x зависит только от расстояния z до горизонтальной плоскости отсчета.

В этих условиях касательные напряжения возникают лишь на поверхностях dFверхней и нижней граней элементарного параллелепипеда, причем dF=dxdy. Если касательное напряжение на нижней грани параллелепипеда равно τ, то на верхней оно составляет (τ+(∂τ/∂z)dz). Производная (∂τ/∂z) выражает изменение касательного напряжения вдоль оси z в точках, лежащих на нижней грани параллелепипеда, а (∂τ/∂z)dz представляет собой изменение этого напряжения вдоль всей длины dz ребра параллелепипеда.

Проекция равнодействующей сил трения на ось x:

τdxdy-(τ+(∂τ/∂z)dz)dxdy=-(∂τ/∂z)dxdydz;

Подставив в это выражение значение касательного напряжения τ, получим: μ*((∂(∂ω_x/∂z))/∂z)dxdydz=μ*(∂²ω_x/∂z²)dxdydz ;

В более общем случае трехмерного потока составляющая скорости ω_x будет изменяться не только в направлении z, но и в направлениях всех трех осей координат. Тогда проекция равнодействующей сил трения на ось x примет вид: μ*(∂²ω_x/∂z²+∂²ω_x/∂y²+∂²ω_x/∂x²)dxdydz. Выражение в скобках называется оператором Лапласа и обозначают ▼. Тогда проекции на оси x,y и z равны:

На ось x : μ*▼²ω_xdxdydz;

На ось y : μ*▼²ω_ydxdydz;

На ось z : μ*▼²ω_zdxdydz;

Суммы проекций сил на оси координат, в соответствии с основным принципом динамики, должны быть равны произведению массы жидкости на проекции ускорения на оси координат. Поэтому, учитывая силы давления, получаем:

ρ*dω_x/dτ=-∂p/∂x+μ*▼²ω_x

ρ*dω_y/dτ=-∂p/∂y+μ*▼²ω_y

ρ*dω_z/dτ=-ρg-∂p/∂z+μ*▼²ω_z

Эти уравнения представляют собой уравнения Навье — Стокса, описывающие движение вязкой капельной жидкости.

Левые части этих уравнений выражают произведение массы единицы объема ρ на проекцию ее ускорения, т. е. представляют собой проекции равнодействующей сил инерции, возникающих в движущейся жидкости.

В правых частях тех же уравнений произведение ρg отражает влияние сил тяжести, частные производные ∂p/∂x, ∂p/∂y и ∂p/∂z - влияние изменения гидростатического давления, а произведения вязкости на сумму вторых производных проекций скорости — влияние сил трения на движущуюся жидкость.

При движении идеальной жидкости, когда силы трения отсутствуют, при подстановке μ = 0 в уравнения Навье-Стокса последние совпадают с уравнениями Эйлера, т. е. уравнения движения Эйлера можно получить как частный случай уравнений Навье—Стокса.

Смысл: описывает закон сохранения импульса или баланс кол-ва движ-я.

19. Сущность теории подобия. Теория подобия является учением о методах научного обобщения эксперимента. Она указывает, как надо ставить опыты и как обрабатывать их результаты, чтобы при проведении небольшого числа экспериментов иметь возможность обобщать опытные данные, получая единые уравнения для всех подобных явлений. Применение теории подобия часто позволяет вместо дорогостоящих трудоемких опытов на промышленной аппаратуре выполнять исследования на моделях значительно меньшего размера; помимо этого, опыты можно проводить не с рабочими (часто вредными и опасными) веществами и не в жестких (высокие температуры, сильно агрессивные среды) условиях реального производственного процесса, а с другими (модельными) веществами в условиях, отличающихся от пром-ых. Таким образом, методы теории подобия лежат в основе масштабировании и моделирования процессов. В широком смысле под моделированием понимают метод исследования, при котором вместо непосредственно интересующего нас процесса или явления, протекающего в каком-то объекте (натуре), изучается соответствующий процесс на другом объекте (модели). Следует отметить, что в литературе под термином «модель» не всегда понимают материальную модель, на которой проводятся исследования. Часто моделью считают некоторую познавательную, или мысленную, физическую или математическую модель, т. е.. схему, с той или иной степенью точности отражающую наиболее существенные стороны изучаемого процесса. Такие модели, которые в отличие от материальных можно также назвать идеальными, кладут в основу исследования данного процесса или явления. Примерами могут служить модели структуры потоков в аппаратах, модели массопередачи и др., рассматриваемые в настоящем курсе. На основе принятой идеальной физической модели составляют соответствующую ей математ. модель, т. е. математ. описание процесса. Однако под терминами «модель» и «моделирование» подразумеваются в основном материальное моделирование и материальные модели. Физическое моделирование- моделирование, при котором в опытах на модели меняются (по сравнению с производственными условиями) лишь масштаб установки, используемые вещества, температурные условия и т. п., но физическая сущность изучаемого в модели процесса остается той же, что и у моделируемого процесса (в натуре). Вместе с тем методы теории подобия часто применяются и при использовании других видов моделирования, в которых моделирующие процессы отличаются от моделируемых по физической природе. Важнейшим из них является математическое моделирование, при котором различные процессы воспроизводятся на электрических моделях — электронных вычислительных машинах. Однако, используя методы теории подобия, надо иметь в виду, что теория подобия не может дать больше того, что содержится в исходных уравнениях, описывающих исследуемый процесс. Если исходные уравнения неверно описывают физическую сущность процесса, то и конечные результаты, полученные при использовании методов теории подобия, будут неправильными. В настоящее время моделирование активно исп-ся при изучении многих пр-сов.	20. Условия подобия. Один из основных принципов теории подобия заключается в выделении из класса явлений группы подобных явлений.Подобными называют явления, для которых постоянны отношения характеризующих их сходственных величин. Так, существуют геометрическое, временное подобие, подобие физических величин, подобие скоростей и т.д. Безразмерные масштабные множители, выражающие отношения однородных сходственных подобных параметров (линейных размеров, времени, скоростей, физических величин и т.д.), называются константами подобия (k). Константы подобия,выражающие отношения различных одноименных величин в натуре и в модели, постоянны для различных сходственных точек подобных систем, но изменяются в зависимости от соотношения размеров натуры и модели. Подобие потоков в натуре и модели можно охарактеризовать также с помощью инвариантов (i) подобия, выражая все подобные величины в относительных единицах, т. е. в виде отношений сходственных величин в пределах каждой системы. Инварианты подобия могут быть неодинаковы для различных сходственных точек, подобных систем, но не зависят от соотношения размеров натуры и, модели.Это означает, что при переходе от одной системы к другой, ей подобной, инварианты подобия не меняют своих значений. Однако инварианты подобия могут быть выражены также отношениями разнородных величин, т. е. представлять собой безразмерные комплексы этих величин. Например, таковым является критерий Рейнольдса: Re=(ω’d’ρ’)/μ’=(ω”d”ρ”)/μ”.	21. Основные критерии гидродинамического подобия. Диф. ур-я Навье—Стокса невозможно решить для большинства практически важных случаев. Теория подобия позволяет преобразовать Ур-я Навье—Стокса и получить из них некоторую общую функциональную зависимость между критериями подобия, характеризующими силы, действующие при движении вязкой жидкости. Ур-е Навье—Стокса для капельной жидкости в развернутом виде для. одной из осей — вертикальной оси z: ρ(∂wz/∂τ + wx∂wz/∂x + wy∂wz/∂y + wz∂wz/∂z)= = -ρg - ∂p/∂z + μ(∂2wz/∂x2 + ∂2wz/∂y2 + ∂2wz/∂z 2) критерии подобия можно получить путем деления одной части диф. ур-я на другую и последующего отбрасывания знаков математических операторов. Если движение жидкости установившееся, то ∂wz/∂τ = 0. При этом, заменяя в левой части уравнения, характеризующей силу инерции, дифференциалы конечными величинами, находим ρ(wx∂wz/∂x + wy∂wz/∂y + wz∂wz/∂z) ρw*w/l = ρw2/l где l — определяющий линейный размер. ρg отр-т действие силы тяжести, ∂p/∂z (хар-т действие силы давления) p/l . Последнее слагаемое правой части, отражающее действие силы трения μ(∂2wz/∂x2 + ∂2wz/∂y2 + ∂2wz/∂z 2) μw/l2 Разделим члены одной части Ур-я на члены другой его части и найдем т. о. выр-я, хар-щие соотн-я м/у соотв-ми силами и силой инерции, выразим эти силы в относительных единицах, приняв за масштаб силу инерции. В результате получим безразмерные соотношения величин — критерии подобия. Выр-е, хар-щее отношение силы тяжести к силе инерции, имеет вид ρg/(ρw2/l) = gl/w2 Безразмерный комплекс gl/w2 представляет собой критерий Фруда и обозначается через Fr: Fr = w2/gl Критерий Фруда отражает влияние сил тяжести, или собственного веса, на движение жидкости, он является мерой отношения силы инерции к силе тяжести в подобных потоках. Соот-е м/у силами давления и инерции может быть охар-но выр-ем (p/l)/(ρw2/l) = p/ρw2 p/ρw2 наз. критерием Эйлера и обоз. ч/з Eu: Eu = ∆p/ρw2 Критерий Эйлера отражает влияние перепада гидростатического давления па движение жидкости. Он характеризует отношение изм-я силы гидростатического давления к силе инерции в подобных потоках. Найдем выр-е, явл-ся мерой отн-я силы трения к силе инерции. (ρw2/l)/(μw/l2) = wlρ/μ = Re Критерий Рейнольдса отражает влияние силы трения на движение жидкости. Он характеризует отношение инерционных сил к силам трения в подобных потоках. Величина l в критерии Re предс-т собой опр-щий линейный размер. При движении жидкости через трубопроводы или аппараты за такой размер прин-ся их диаметр d, а в случае некруглого сечения потока - эквивалентный диаметр dэ. При неуст-ся дв-и жид-ти в уравнении Навье - Стокса ∂wz/∂τ ≠ 0. Заменим ρ∂wz/∂τ ρw/τ, охарактеризуем сотн-е м/у силой инерции и этой вел-ной: (ρw2/l)/( ρw/τ) = w τ /l Ho = w τ /l – критерий гомохромности, учитывает неуст-ся хар-р движ-я в подобных потоках. γ(Ho, Fr, Eu, Re) = 0 – обобщенное (критериальное) ур-е гидродинамики.
22.Основные принципы метода анализа размерностей. Многие процессы хим. тех-гии зависят от большого числа разл-х факторов, что для них не удается получить полного мат. описания; можно лишь в самом общем виде представить зависимость между различными переменными, влияющими на протекание процесса. Согласно практ-м данным, нек-я вел-на α зависит от параметров β, δ,θ, то общий вид зависимости между данными величинами φ(γ,α,β,δ,θ) = 0 Для нахождения расчетного уравнения, может быть применен метод анализа размерностей. В основу метода -положена π-теорема Бэкингема: общую функц-юзав-ть, связывающую м/у собой n переменных величин, при m основных единицах их измерения, можно представить в виде зависимости между (n-m) безразмерными комплексами этих величин, а при наличии подобия — в виде связи между (n-m) критериями подобия. Для пользования методом анализа разм-тей необх-мо знать какие переменные должны входить в зав-ть общего вида типа зав-ти.	23. Гидравлические сопротивления в трубопроводах. Потери напора в трубопроводе в общем случае обусловливаются сопротивлением трения и местными сопротивлениями. Сопр-е трения называемое также сопр-ем по длине, существует при движении реальной жидкости по всей длине трубопровода. На него ок-ет влияние режим течения жид-ти (ламинарный, турбулентный, степень развития турбулентности). Местные сопр-я возникают при любых изм-ях зн-я ск-типотока или ее напр-я (вход потока в трубу и выход из нее жидкости, внезапные сужения и расширения труб, отводы, колена, тройники, запорные и регулирующие-устройства (краны, вентили, задвижки) и др. Потерянный напор: hп = hтр + hмс В случае ламинарного дв-я по прямой трубе потеря напора на трение (т. е. его потеря по длине) hтр может быть определена теоретически на основании уравнения Пуазейля (Vc = πd4∆F/128μl). Согласно, Ур-ю Бернулли, для гориз-го трубопровода (z1=z2) постоянного сечения (w1 = w2) напор, теряемый на трение (p1-p2)/ρg = ∆p/gρ = hтр; ∆p = gρhтр wπd2/4 = ρd4ghтр/128μl; hтр = 32wμl/ρd2g = 64μ/wρd*l/d*w2/2g = 64/Re*l/d*w2/2g; hск = w2/2g – скоростной поток. Величину, показывающую, во сколько раз напор, потерянный на трение, отличается от скоростного напора, называют коэффициентом потерь энергии по длине, или коэффициентом сопротивления по длине, или коэффициентом сопротивления трения, и обозначают символом ζтр, а отношение 64/Re, входящее в эту величину, — коэффициентом трения: λ = 64\Re; ζтр = λl/d; hтр = ζтрw2/2g; ∆pтр = λl/d*w2/2g; Ламинарный режим (Re < 2320): вел-на λ не зависит от шероховатости стенок. (при ламинарном движении потеря напора на трение пропорциональна скорости жидкости в первой степени) λ = B\Re; B – коэф., зав. от формы попереч. сечения. Турбулентный режим: при турбулентном движении эта потеря напора в большей мере зависит от скорости - потерянный напор пропорционален w1.75. Eu = 0.158 Re-0.25(l/d); Eu = ρghтр/ρw2; hтр = 0,316Re-0.25(l/d)*w2/2g; λ = 0.316/ 4√Re; При возрастании Rе величина δ уменьшается. Когда она становится сравнимой с абсолютной шероховатостью (δ≈∆) и меньше ее (δ<∆), вязкий подслой уже не покрывает выступов шероховатости. В таких условиях коэффициент трения все больше начинает зависеть от шероховатости. При этом величина Re, а следовательно, и потеря напора на трение возрастают под действием сил инерции, возникающих вследствие дополнительного вихреобразования вокруг выступов шероховатости. С увеличением критерия Рейнольдса зона гладкого трения, в которой λ зависит лишь от Rе, переходит сначала в зону смешанного трения, когда на величину λвлияют и Rе и шероховатость, а затем в автомодельную {по отношению к Rе) зону, когда величина λ практически перестает зависеть от критерия Рейнольдса и определяется лишь шероховатостью стенок труб. Автомодельную область называют также областью квадратичного закона сопротивления, при отсутствии влияния Rе (т. е. скорости) -на величину λ, сопротивление трения становится пропорциональным квадрату скорости. Критические значения Rекр1, при которых шероховатость начинает влиять на коэффициент трения, а также критические значения Rекр2, при которых λ, становится функцией только шероховатости трубы, зависят от относительной шероховатости ε, выражаемой отношением абсолютной шероховатости ∆ к диаметру d. трубы: ε = ∆/d; Rекр1 = 23/ε; Rекр2 = 220ε-9/8; При расчете коэффициента трения для всех областей (зон) турбулентного движения применимо общее уравнение: 1/λ = -2lg[ε/3.7 + (6.81/Re)0.9] Данные зависимости справедливы для изотермических условий. Определение hмс: Потери напора в местных сопротивлениях, как и потери на трение, выражают через скоростной напор. Отношение потери напора в данном местном сопротивлении hмс к скоростному напору hск = w2/2g называют коэффициентом местного сопр-я и (ζмс). hvc = Σ ζмс *w2/2g Расчетное уравнение для определения общей потери напора может быть представлено в виде hп = ζтрw2/2g + Σζмсw2/2g = Σζw2/2g Потеря напора находится по уравнению: hп = (λl/dэ + Σζмс ) w2/2g Потеря давления: ∆p = ( λl/ dэ + Σζмс) ρw2/2; Уравнение для расчета общих потерь напора на трение и местные сопротивления имеет вид: hп = λ(l/d + Σn)w2/2g, n – коэф. опр-й опыт. путем.	24. Расчет диаметра трубопроводов. При заданной производительности диаметр трубопровода может быть вычислен исходя из уравнения расхода: Vсек = wS = wπd2/4; d = √4Vсек/πw; Таким образом, размер диаметра трубопровода однозначно определяется выбором значения скорости движущейся в нем жидкости. .Чем выше выбранная скорость w, тем меньше, потребный диаметр трубопровода, т. е. тем меньше затраты материала на его изготовление, а значит, его стоимость, а также стоимость монтажа и ремонта трубопровода. Вместе с тем при увеличении скорости, в соответствии с уравнением, растут потери напора в трубопроводе, т. е. увеличивается перепад давления, требуемый для перемещения жидкости, и, следовательно, возрастают затраты энергии на ее перемещение. При оптимальном диаметре трубопровода обеспечиваются минимальные затраты на его эксплуатацию. На основе технико-экономических соображений установлены рекомендуемые пределы изменения скоростей жидкостей, газов и паров в промышленных трубопроводах. Значения этих скоростей приведены ниже. Скорости движения -маловязких капельных жидкостей не должны превышать 3 м/сек; для вязких капельных жидкостей 1 м/сек. При движении капельных жидкостей самотеком скорости их обычно составляют 0,2—1 м/сек, а в нагнетательных трубопроводах (при перекачке насосами) — 1—3 м/сек. Скорости газов и паров колеблются в следующих пределах: для газов при сравнительно небольших избыточных давлениях (например, развиваемых вентиляторами) — 8—15 м/сек, для газов под давлением— 15— 25 м/сек, для насыщенного водяного пара — 20—30 м/сек и для перегретого водяного пара — 30—50 м/сек.	25.Основные параметры насосов.	26. Классификация насосов. Насосы — гидравлические машины, которые преобразуют механическую энергию двигателя в энергию перемещаемой жидкости, повышая ее давление. Разность давлений жидкости в насосе и трубопроводе обусловливает ее перемещение. Различают насосы двух основных типов: динамические и объемные. В динамических насосах жидкость перемещается при воздействии сил на незамкнутый объем жидкости, который непрерывно сообщается со входом в насос и выходом из него. В объемных насосах жидкость перемещается (вытесняется) при периодическом изменении замкнутого объема жидкости, который периодически сообщается со входом в насос и выходом из него. Динамические насосы по виду сил, действующих на жидкость, подразделяются на лопастные и насосы трения. К лопастным относятся динамические насосы, в которых энергия передается жидкости при обтекании лопастей вращающегося рабочего колеса (или нескольких колес) насоса. Лопастные насосы, в свою очередь, делятся на центробежные и осевые, причем в центробежных насосах жидкость движется через рабочее колесо от его центра к периферии, а в осевых — в направлении оси колеса; Насосы трения представляют собой динамические насосы, в которых жидкость перемещается преимущественно под воздействием сил трения. К насосам трения относятся, в частности, вихревые и струйные насосы. Группа объемных насосов включает насосы, в которых жидкость вытесняется из замкнутого пространства телом, движущимся возвратно-поступательно (поршневые, плунжерные, диафрагмовые насосы) или имеющим вращательное движение (шестеренные, пластинчатые, винтовые насосы).