Шпоры(Процессы и аппараты). 1. Классификация основных процессов

• Название: 1. Классификация основных процессов
• Анкор: Шпоры(Процессы и аппараты).docx
• Дата: 18.05.2017
• Размер: 428.64 Kb.
• Имя файла: Шпоры(Процессы и аппараты).docx
• Тип: Документы; #7827
• страница: 2 из 3

12. Некоторые практические приложения уравнения Бернулли.

1.Принципы измерения скорости и расхода жидкости.

Для определения скоростей и расходов жидкостей обычно применяются дроссельные приборы и пневмометрические трубки.

Принцип работы пневмометрических трубок, например трубки Пито—Прандтля заключается в том, что в каждом сечении разность уровней жидкости в трубках выражает скоростной напор h_ск в точке сечения, лежащей на оси трубы.

Разность уровней рабочей жидкости в трубках удобнее измерять не посредством пьезометрических трубок, а при помощи дифференциального манометра (рис. 1). Его U-образная трубка заполнена жидкостью, которая не смешивается с рабочей и имеет значительно большую плотность, чем последняя. Это позволяет измерять перепады давлений в случае значительного избыточного давления (или вакуума) в трубопроводе при относительно небольшой высоте прибора.
По результатам измерении h_ск= ω²/(2g)находят максимальную скорость жидкости вдоль оси трубопровода. Для определения средней скорости жидкости либо снимают эпюру распределения скоростей по сечению трубопровода, передвигая пневмометрическую трубку в различные точки сечения.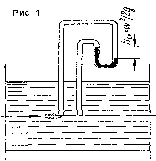

Такой способ определения скорости и расхода жидкости прост, но недостаточно точен из-за трудности установки пневмометрических трубок строго вдоль оси трубопровода.

Более широко распространено определение скоростей и расходов жидкостей с помощью дроссельных приборов, принцип работы которых основан на измерении перепада давлений при изменении поперечного сечения трубопровода. В качестве дроссельных приборов используют мерные диафрагмы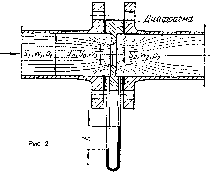

Мерная диафрагма (рис. 2) представляет собой тонкий диск с отверстием круглого сечения, центр которого расположен на оси трубы.

Считая трубопровод горизонтальным, запишем для двух сечений, перепад давлений между которыми измеряется дифференциальным манометром, уравнение Бернулли. В соответствии с обозначениями на рис. 2 и пренебрегая потерей напора, имеем:

p₁/ρg+ω²₁/(2g)=p₂/ρg+ω²₂/2g; Откуда ω²₂/2g - ω²₁/(2g)=(p₁-p₂)/ρg=h; h- перепад давлений.

Т.к. ω₁=ω₂*S₂/S₁= ω₂*d²₂/d²₁, то ω₂=((2gh)/(1-(d₂/d₁)⁴)) ^1/2; Тогда объемный расход жидкости: Q=(απ/4)*d²₀*((2gh)/(1-(d₂/d₁)⁴)) ^1/2 ;

Коэффициент α называется коэффициентом расхода дроссельного прибора. Его значение зависит от значения критерия Рейнольдса для жидкости и от отношения диаметра отверстия дроссельного прибора к диаметру трубопровода: α=f(Re,d₀/d₁).

Величиной (d₂/d₁)⁴ в уравнении для Q можно в первом приближении пренебречь, поэтому:

Q= απ/4*d²₀*(2gh) ^½;

Среднюю скорость движения жидкости в трубопроводе определяют, разделив Q на площадь сечения трубопровода: ω=α*(d₀/d) ² *(2gh) ^1/2. 2.Истечение жидкостей. Определим расход жидкости при ее истечении через круглое отверстие в тонком днище открытого сосуда, в котором поддерживается постоянный уровень Hжидкости (рис. 3).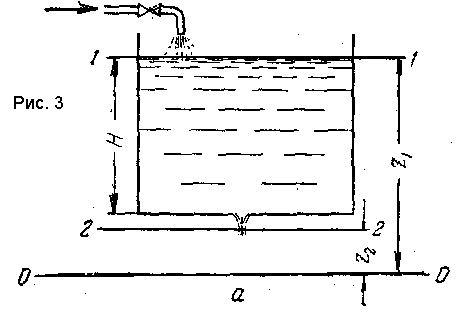

Выбрав плоскость сравнения 0-0 параллельной днищу сосуда, напишем уравнение Бернулли (считая жидкость идеальной) для сечения 1-1, соответствующего верхнему уровню жидкости в сосуде, и сечения 2-2, плоскость которого проходит через указанное сжатое сечение вытекающей струи:

ω²₁/(2g)+p₁/(ρg)+z₁ = ω²₂/(2g)+p₂/(ρg)+z₂;

Для открытого сосуда p₁=p₂; кроме того, при постоянном уровне жидкости скорость ее ω₁=0. Пренебрегая небольшим расстоянием от плоскости отверстия в днище сосуда до плоскости сжатого сечения струи, можно принять, что z₁-z₂≈H. Отсюда ω²=(2gH) ^1/2.

Объемный расход: Q= ω₂*S₂=φ*(2gH) ^1/2*ε*S₀ или Q= α*S₀*(2gH)^1/2 (1), где ε - коэф-т сжатия струи. Коэффициент α представляет собой коэффициент расхода и выражается произведением коэффициентов скорости и сжатия струи: α=φ*ε;

Из уравнения (1) следует, что расход жидкости, вытекающей через отверстие в тонком днище, зависит от высоты постоянного уровня жидкости над отверстием и от размера отверстия, но не зависит от формы сосуда.

13. Гидравлический радиус и эквивалентный диаметр.

При движении жидкости через сечение любой формы, отличной от круглой, в качестве расчетного линейного размера принимают гидравлический радиус или эквивалентный диаметр.

Под гидравлическим радиусом r_Г (м) понимают отношение площади затопленного сечения трубопровода или канала, через которое протекает жидкость, т. е. живого сечения потока, к смоченному периметру: r_Г=S/П;

где S — площадь сечения потока жидкости, м²; П — смоченный периметр, м.

Для круглой трубы с внутренним диаметром dи, значит, площадью свободного сечения S=(πd²)/4 при сплошном заполнении его жидкостью П=πd,откуда гидравлический радиус:

r_Г=S/П=((πd²)/4)/(πd)=d/4;

Диаметр, выраженный через гидравлический радиус, представляет собой эквивалентный диаметр: d=d_Э=4*r_Г;

Следовательно: d_Э=(4S)/П;

Эквивалентный диаметр равен диаметру гипотетического трубопровода круглого сечения, для которого отношение площади S к смоченному периметру П то же, что и для данного трубопровода некруглого сечения.

Для канала прямоугольного сечения со сторонами a и b, полностью заполненного жидкостью, гидравлический радиус: r_Г=S/П=ab/(2(a+b)), а эквивалентный диаметр d_Э=4*r_Г=(2ab)/(a+b)

Для канала кольцевого поперечного сечения, в котором жидкость ограничена внутренней и наружной окружностями с диаметрами d_в и d_н соответственно, эквивалентный диаметр:

d_Э=(4S)/П= d_Н-d_В

Для круглой трубы: d_Э=d.

14.Режимы движения жидкости, их характеристики.

Движение, при котором все частицы жидкости движутся по параллельным траекториям, называют струйчатым, или ламинарным.

Если скорость воды в трубе 2 увеличивать сверх определенного предела, то окрашенная струйка сначала приобретает волнообразное движение, а затем начинает размываться, смешиваясь с основной массой воды. Это объясняется тем, что отдельные частицы жидкости движутся уже не параллельно друг другу и оси трубы, а перемешиваются в поперечном направлении.

Такое неупорядоченное движение, при котором отдельные частицы жидкости движутся по запутанным, хаотическим траекториям, в то время как вся масса жидкости в целом перемещается в одном направлении, называют турбулентным.

В турбулентном потоке происходят пульсации скоростей, под действием которых частицы жидкости, движущиеся в главном (осевом) направлении, получают также поперечные перемещения, приводящие к интенсивному перемешиванию потока по сечению и требующие соответственно большей затраты энергии на движение жидкости, чем при ламинарном потоке.

Опыт показывает, что переход от ламинарного течения к турбулентному происходит тем легче, чем больше массовая скорость жидкости ρωи диаметр трубы d, и чем меньше вязкость жидкости μ. Рейнольдc установил, что указанные величины можно объединить в безразмерный комплекс ωdρ/μ, значение которого позволяет судить о режиме движения жидкости. Этот комплекс носит название критерия Рейнольдcа (Rе): Re=ωdρ/μ

КритерийRе является мерой соотношения между силами вязкости и инерции в движущемся потоке.В самом деле, вероятность нарушения ламинарного режима течения и возникновения хаотического перемещения частиц тем больше, чем меньше вязкость жидкости, препятствующая этому нарушению, и чем больше ее плотность, представляющая собой меру инерции отклонившихся от прямолинейного движения частиц. Поэтому при равных скоростях движения различных жидкостей в трубах одинакового диаметра турбулентность возникнет тем легче, чем больше ρ и меньше μ, или чем меньше кинематическая вязкость ν=μ/ρ. Соответственно критерий Рейнольдса может быть записан в виде: Rе = (ωd)/ν.

Переход от ламинарного к турбулентному движению характеризуется критическим значением Rе_кр. Так, при движении жидкостей по прямым гладким трубам Rе_кр≈2320. При Rе<2320 течение обычно является ламинарным, поэтому данную область значений Rе называют областью устойчивого ламинарного режима течения. При Rе>2320 чаще всего наблюдается турбулентный характер движения. Однако при 2320 10 000 турбулентное движение становится устойчивым (развитым).

Указанное значение Rе_кр=2320 является условным, так как оно относится лишь к стабилизированному изотермическому потоку в прямых трубах с очень малой шероховатостью стенок. Наличие различных возмущений, обусловленных шероховатостью стенок трубы, изменением значения скорости потока или ее направления, близостью входа в трубу и т. п., может существенно снижать величину Rе_кр. Критическое значение Rе уменьшается и при неизотермичности потока по сечению трубы из-за возникновения конвективных токов жидкости в направлении, перпендикулярном к оси трубы.

В случае движения жидкости через каналы некруглого сечения при расчете критерия Rе вместо dиспользуют эквивалентный диаметр.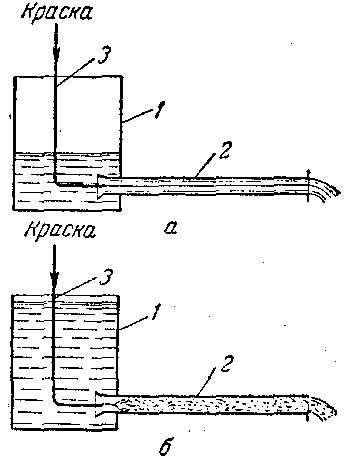

15. Распределение скоростей жидкости при установившемся ламинарном потоке.

В случае ламинарного движения вязкой жидкости в прямой трубе круглого сечения всю жидкость можно мысленно разбить на ряд кольцевых слоев, соосных с трубой. Вследствие действия между слоями сил трения слои будут двигаться с неодинаковыми скоростями. Центральный цилиндрический слой у оси трубы имеет максимальную скорость, но, по мере удаления от оси, скорость элементарных кольцевых слоев будет уменьшаться. Непосредственно у стенки жидкость как бы «прилипает» к стенке, и ее скорость здесь обращается в нуль.

Выделим в потоке жидкости, ламинарно движущемся по трубе радиусом R (рис. 1),цилиндрический слой длиной l и радиусом r.

Движение слоя происходит под действием разности сил давления P₁ и Р₂ с обеих торцовых сторон цилиндра: P₁-P₂=(p₁-p₂)*πr², где P₁ и P₂ — гидростатические давления в сечениях 1-1и 2-2.

Движению цилиндра оказывает сопротивление сила внутреннего трения T, для которой, справедливо выражение: |T|= -μF*dω_r/dr

гдеω_r — скорость движения жидкости вдоль оси цилиндранарасстоянииr от оси;F=2πrl - наружная поверхность цилиндра; μ - вязкость жидкости.

Знак минус указывает на убывание скорости с увеличением радиусаr (при r=R величина ω_r=0).

При установившемся движении разность сил давления P₁—Р₂ затрачивается на преодоление силы трения Т, и сумма проекций всех этих сил на ось потока должна быть равна нулю. Вследствие трения движение рассматриваемого цилиндрического слоя тормозится, значит, сила трения, приложенная к его боковой поверхности, направлена противоположно разности Р₁ — Р₂ и проектируется на ось, направление которой совпадает с направлением движения, со знаком минус. Следовательно

(p₁-p₂)/πr²=-(-μF*dω_r/dr)=0

Интегрируем, разделяя переменные, полученное уравнение в следующих пределах: ∫((p₁-p₂)/(2μl)*rdr)[от r до R]= -∫dω_r [от w_r до 0]

тогда: ω_r=(p₁-p₂)/(4μl)*(R²-r²);

Скорость имеет максимальное значение на оси трубы, гдеr=0: ω_max=(p₁-p₂)/(4μl)*R²;

Тогда получим: ω_r=ω_max*(R²-r²)/R²=ω_max*(1-r²/R²);

Последнее уравнение представляет собой закон Стокса, выражающийпараболическое распределение скоростей в сечении трубопровода при ламинарном движении.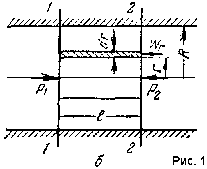

16. Расход жидкости при установившемся ламинарном потоке(уравнение Пуазейля).

Для определения расхода жидкости при ламинарном движении рассмотрим элементарное кольцевое сечение (рис. 1) свнутренним радиусом r и внешним радиусом (r+dr), площадь которого равна dS=2πrdr. Объемный расход жидкости через это сечение составляет: dQ=ω_rdS=ω_r2πrdr или

dQ=(p₁-p₂)/(4μl)*(R²-r²)*2πrdr.

Интегрируя последнее уравнение получаем общий расход:

Q=(p₁-p₂)/(8μl)*πR⁴.

Подставляя вместо R диаметр трубы d=2R и обозначая (p₁-p₂)=Δp, окончательно находим:

Q=πd⁴Δp/(128μl);

Это уравнение определяющее расход жидкости при ее ламинарном движении по круглой прямой трубе, носит название уравнения Пуазейля.

Соотношение между средней скоростью ωи максимальной скоротью ω _max:

Q= ωS= ωπR² и

πR²ω=(p₁-p₂)/(8μl)*πR⁴, откуда

ω=(p₁-p₂)/(8μl)*R²;

ω=ω _max /2;

Таким образом, при ламинарном потоке в трубе средняя скорость жидкости роена половине скорости по оси трубы.

Соответственно параболический закон распределения скоростей по сечению трубы может быть представлен в виде: ω= 2ω(1-r²/R²);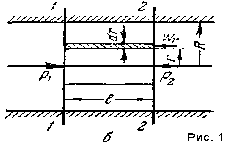

17. Некоторые характеристики турбулентного потока.

В промышленной практике наиболее распространено турбулентное движение жидкостей.

Опыт показывает, что средняя скорость ω при турбулентном движении не равна половине максимальной (как для ламинарного движения), а значительно больше, причем ω/ω_max = f(Rе). Например, при Rе = 10⁴ скорость ω≈0,8ω_max , а при Rе = 10⁸ величина ω≈0,9ω_max.

Строго теоретически не удается получить профиль распределения скоростей и значение ω/ω_max из-за сложного характера турбулентного движения.

В каждой точке турбулентного потока истинная скорость не остается постоянной во времени из-за хаотичности движения частиц. Ее мгновенные значения испытывают флуктуации, или нерегулярные пульсации, носящие хаотический характер.

Типичная картина изменения составляющей истинной мгновенной скорости ω_x (вдоль оси xпотока) для некоторой точки в зависимости от времени τ представлена на рис. 1. Для данной точки осредненная во времени скорость ω_x, может быть найдена из соотношения: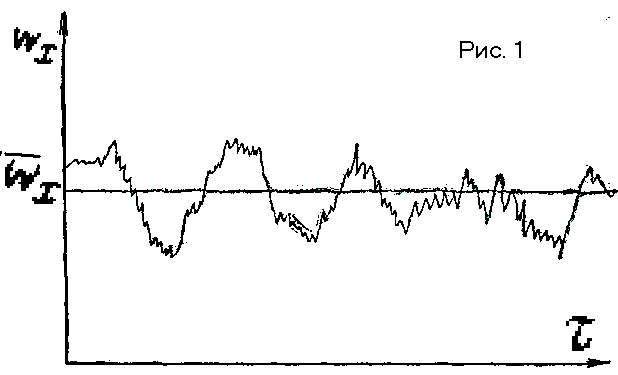

ω_x= ( ∫ ω_xdτ )/ τ [от 0 до τ]

Разность между истинной и осредненной скоростями называют мгновенной пульсационной скоростью и обозначают через ∆ω: ω-ω=∆ω. величина ∆ω имеет переменный знак, поэтому ω=ω±∆ω.

Понятие осредненной скорости ω не следует путать с введенным ранее понятием средней скорости ω. Последняя представляет собой не среднюю во времени скорость в данной точке, а скорость, осредненную для всего поперечного сечения трубопровода.

Турбулентное движение по существу не является установившимся, т.е. осреднение скоростей во времени позволяет приближенно считать это движение стационарным. В этом смысле турбулентное движение может рассматриваться как квазистационарное.

Интенсивность турбулентности выражается отношением:

I_т=∆ω/ω;

Интенсивность турбулентности является мерой пульсаций в данной точке потока. При турбулентном течении по трубам I_т ≈ 0,01 — 0,1.

Если средние пульсации скорости одинаковы по всем направлениям, то такая турбулентность называется изотропной.

Помимо интенсивности I_т другими важными характеристиками турбулентного движения являются масштаб турбулентности и турбулентная вязкость.

Чем ближе друг к другу находятся две частицы жидкости в турбулентном потоке, тем более близки их истинные (мгновенные) скорости. В тоже время у достаточно удаленных одна от другой частиц совсем нет связи между колебаниями, или пульсациями, их скоростей. Достаточно близко расположенные частицы, движущиеся совместно, можно считать принадлежащими к некоторой единой совокупности, называемой обычно вихрем. Размер таких вихрей, или глубина их проникания до разрушения, которая приближенно может быть отождествлена с расстоянием между двумя ближайшими частицами, уже не принадлежащими к одному вихрю, зависит от степени развития турбулентности в потоке, или ее масштаба, и поэтому носит название масштаба турбулентности.

Для характеристики турбулентной вязкости рассмотрим две частицы жидкости в турбулентном потоке, движущемся в направлении оси xпараллельно оси трубы. Пусть расстояние между частицами в направлении, перпендикулярном оси трубы, равно dy.Составляющие скорости частиц по направлению потока ω_x,1 и ω_x,2отличаются друг от друга на dω_x причем вследствие разности скоростей возникает касательное напряжение τ_н :

τ_н=-μ(dω_x)/dy=-ρν(dω_x)/dy,

где μ и ν— динамическая и кинематическая вязкости; ρ - плотность жидкости; индекс «н» при τозначает «ньютоновское»,

В ламинарном потоке τ_н было бы единственным напряжением, возникающим между расположенными на расстоянии dy слоями жидкости. Однако в турбулентном потоке частицы жидкости перемещаются относительно друг друга не только в продольном (вместе с потоком), но и в поперечном направлении. Это создает дополнительное касательное напряжение τ_т (индекс «т» — турбулентное), которое по аналогии с τ_н можно выразить уравнением: τ_т=-ρν_т(dω_x)/dy

Величину ν_т называют коэффициентом турбулентной вязкости, или просто турбулентной вязкостью.

Турбулентная вязкость, в отличие от обычной вязкости, не является физико-химической константой, определяемой природой жидкости, ее температурой и давлением. Турбулентная вязкость зависит от скорости жидкости и других параметров, обусловливающих степень турбулентности потока (в частности, расстояния от стенки трубы и т. д.).

Суммарное касательное напряжение в потоке определяется, следовательно, как вязкостью жидкости, так и турбулентностью потока: τ=τ_н+τ_т .