ответы по терверу по 37. 1. Классификация случайных событий возможные и невозможные события, совместные и несовместные, противоположные и достоверные события. Примеры
 Скачать 4.53 Mb. Скачать 4.53 Mb.
|
|
35. Неравенство Чебышева. Примеры Лемма: Если случайная величина Х имеет конечные математическое ожидание М(Х) и дисперсию Д(Х), то для любого положительного справедливо неравенство Данное неравенство часто дает грубую, не представляющую интереса оценку. Например, пусть , тогда Тем не менее данное неравенство имеет большое теоретическое значение. С его помощью доказываются теоремы и делаются теоретические выводы. 36. Понятие двумерной (n-мерной) случайной величины. Примеры. Одномерные распределения ее составляющих. Условные распределения.        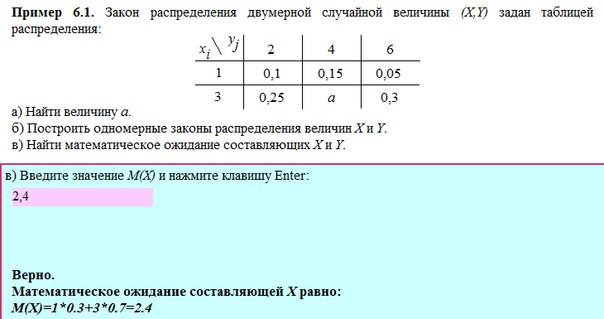  37. Ковариация и коэффициент корреляции случайных величин. Связь между некоррелированностью и независимостью случайных величин  Двумерный нормальный закон распределения.. Систему случайных величин можно интерпретировать как случайную точку на плоскости. Нормальный закон распределения для системы (Х,У) называется двумерным нормальным законом распределения и имеет плотность вероятности 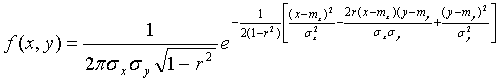 где - математические ожидания соответственно случайных величин Х и У, - средние квадратические отклонения этих величин, r – коэффициент корреляции Х и У. поверхность f(x,y) имеет вид 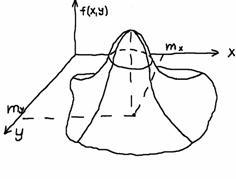 Двумерный нормальный закон распределения имеет, например, точка попадания снаряда из орудия, которое хорошо пристреляно по цели имеющей координаты . Если случайные величины независимы, то r=0 и функция плотности вероятности f(x,y) имеет вид а 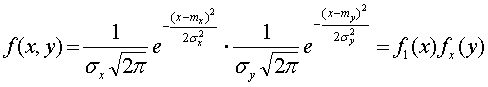 , ,что соответствует упомянутому нами свойству систем независимых случайных величин. Условные математические ожидания и условные дисперсии нормально распределённых величин вычисляются по формулам: Му(х) = ах + (у - ау), Мх(у) = ау + (х - ах),  Dу(Х) = 2х(1 - 2), Dх(У) = 2у(1 - 2). 39.   |
