ответы по терверу по 37. 1. Классификация случайных событий возможные и невозможные события, совместные и несовместные, противоположные и достоверные события. Примеры
 Скачать 4.53 Mb. Скачать 4.53 Mb.
|
29.* Показательный (экспоненциальный) закон распределения, его определение, свойства и примеры. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины X, которое описывается плотностью, имеющей вид 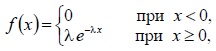 где λ – постоянная положительная величина. где λ – постоянная положительная величина.Свойства: Функция распределения: 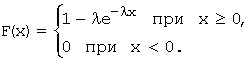 Математическое ожидание: ; дисперсия: ; среднее квадратическое отклонение: . Характерная особенность этого распределения – равенство математического ожидания среднему квадратическому отклонению.
30. Повторные независимые испытания. Формула Бернулли. Примеры Повторными независимыми испытаниями называют испытания, удовлетворяющие следующим условиям: 1) количество n испытаний конечно; 2) вероятность осуществления случайного события А в каждом из испытаний постоянна: Примеры повторных испытаний: 1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну; 2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается). Если вероятность наступления события в каждом испытании постоянна, то вероятность того, что событие наступит ровно раз в независимых испытаниях, равна: Пример. Вероятность попадания в цель при одном выстреле равна 0,7 и не зависит от номера выстрела. Найти вероятность того, что при 5 выстрелах будет ровно 3 попадания в цель. Решение. Подставляем в формулу Бернулли данные задачи и получаем: 31. Понятие о центральной предельной теореме. Локальная и интегральная теоремы Муавра—Лапласа, условия их применимости. Примеры. Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова. Закон распределения суммы независимых случайных величин
где 0;i=1,2,\ldots,n" ALIGN=BOTTOM WIDTH=162 HEIGHT=16 BORDER=0>.
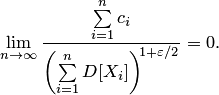 При решении многих практических задач используют следующую формулировку теоремы Ляпунова для средней арифметической наблюдавшихся значений случайной величины , которая также является случайной величиной (при этом соблюдаются перечисленные два условия): если случайная величина имеет конечные математическое ожидания и дисперсию , то распределение средней арифметической 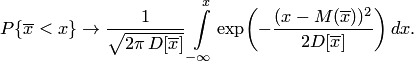 Поэтому вероятность того, что заключена в интервале , можно вычислить по формуле 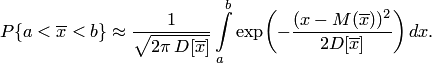 Используя функцию Лапласа, можно записать в удобном для расчётов виде: Где Следует отметить, что центральная предельная теорема справедлива не только для непрерывных, но и для дискретных случайных величин. Практическое значение теоремы Ляпунова огромно. Опыт показывает, что закон распределения суммы независимых случайных величин, сравнимых по своему рассеиванию, достаточно быстро приближается к нормальному. Уже при числе слагаемых порядка десяти закон распределения суммы можно заменить на нормальный. 32.* Следствия из интегральной теоремы Муавра—Лапласа. Примеры. Следствие. Если вероятностьнаступления событияв каждом испытании постоянна и отлична от0 и 1, то при достаточно большом численезависимых испытаний вероятность того, что: а) число т наступлений событияотличается от произведенияне более, чем на величину(по абсолютной величине), т.е . 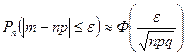 ; ; б) частостьсобытиязаключена в пределах отдо(включительно), т.е. Где 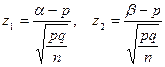 в) частостьсобытияотличается от его вероятностине более, чем на величину(по абсолютной величине), т.е. 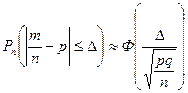 Пример.Вероятность наступления события А в каждом из 900 независимых испытаний равна . Найдите вероятность того, что событие А произойдет: а) 710 раз; б) от 710 до 740 раз. Решение. а) Дано: , , , . Так как б) Дано: , , , , . Так как 33. Асимптотическая формула Пуассона и условия ее применимости. Примеры. Применение формулы Бернулли при больших значениях приводит к произведению очень больших Формула Пуассона Рассмотрим ситуацию, в которой число испытаний в схеме Бернулли неограниченно увеличивается, а вероятность наступления события Доказательство. По формуле Бернулли 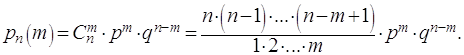 Воспользуемся тем, что по условию или 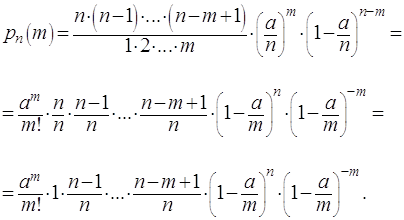 Так как и фиксированы, а стремится к бесконечности, то множители 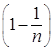 ; … ; ; … ; 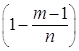 и и 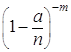 стремятся к единице, а множитель стремятся к единице, а множитель 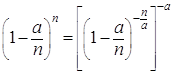 стремится к , то стремится к , тоПолученное выражение называется Пуассоновским приближением формулы Бернулли. Эта формула даёт хорошее приближение при достаточно большом и малом (например, и Вероятность события, заключающегося в том, что появится не более раз, очевидно, вычисляется по формуле 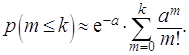 Пример. На предприятии изготовлено и отправлено заказчику 100000 бутылок пива. Вероятность того, что бутылка может оказаться битой, равна 0,0001. Найти вероятность того, что в отправленной партии будет ровно три и ровно пять битых бутылок. Решение. Дано: n = 100000, p = 0,0001, m = 3 (m = 5). Находим Воспользуемся формулой Пуассона 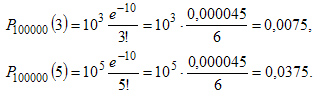 34. Лемма Чебышева. Примеры При изучении теории вероятностей приходится использовать понятия случайного события и случайной величины. При этом предсказать заранее результат испытания, в котором может появиться или не появиться то или иное событие или какое-либо определенное значение случайной величины, невозможно, так как исход испытания зависит от многих случайных причин, не поддающихся учету. При изучении результатов наблюдений над реальными случайными массовыми явлениями также имеют место некоторые закономерности. Следует обратить внимание на то, что они обладают свойством устойчивости. Суть этого свойства состоит в том, что конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате большой массы подобных явлений, а характеристики случайных событий и случайных величин, наблюдаемых в испытаниях, при неограниченном увеличении числа испытаний становятся практически не случайными. Теоремы закона больших чисел устанавливают зависимость между случайностью и необходимостью. Теорема Чебышева: при достаточно большом числе независимых случайных величин Х1, Х2, Х3, ..., Хn, дисперсия каждой из которых не превышает одного и того же постоянного числа В, для произвольного сколько угодно малого числа справедливо неравенство 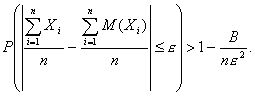 Из теоремы следует, что среднее арифметичес кое случайных величин при возрастании их числа проявляет свойство устойчивости, т. е. стремится по вероятности к неслучайной величине, которой является среднее арифметическое математических ожиданий этих величин, т.е. вероятность отклонения по абсолютной величине среднего арифметического случайных величин от среднего арифметического их математических ожиданий меньше чем на при неограниченном возрастании n стремится к 1, т.е. становится практически достоверным событием. Рассмотрим частный случай теоремы Чебышева: Пусть при n испытаниях наблюдаются n значений случайной величины X, имеющей математическое ожидание M(X) и дисперсию D(X). Полученные значения можно рассматривать как случайные величины Х1, Х2, Х3, ..., Хn,. Это следует понимать так. Серия из п испытаний проводится неоднократно. Поэтому в результате i-го испытания, i=l, 2, 3, ..., п, в каыввввждой серии испытаний появится то или иное значение случайной величины X, не известное заранее. Следовательно, i-e значение xi случайной величины, полученное в i-м испытании, изменяется случайным образом, если переходить от одной серии испытаний к другой. Таким образом, каждое значение xiможно считать случайной величиной Xi . Предположим, что испытания удовлетворяют следующим требованиям: 1) испытания независимы. Это означает, что результаты Х1, Х2, Х3, ..., Хn испытаний—независимые случайные величины; 2) испытания проводятся в одинаковых условиях—это означает, с точки зрения теории вероятностей, что каждая из случайных величин Х1, Х2, Х3, ..., Хn имеет такой же закон распределения, что и исходная величина X, поэтому, MXi=MX и DXi=DX, i=1, 2, .... п. Учитывая вышеуказанные условия, получим Переходя к пределу, имеем Из последнего равенства следует, что среднее арифметическое случайной величины Х обладает свойством устойчивости. Теорема Чебышева имеет большое практическое применение. Она позволяет, используя среднее арифметическое, получить представление о величине математического ожидания, и наоборот. Так, измеряя какой-либо параметр с помощью прибора, не дающего систематической погрешности, можно получить достаточно большое число результатов измерений, среднее арифметическое которых по теореме Чебышева будет практически мало отличаться от истинного значения параметра. Пример. Пусть в результате 100 независимых испытаний получены случайные величины Х1, Х2, …, Х100 с равными математическими ожиданиями М(Х)= 10 и равными дисперсиями D(X)= 1. Оценить вероятность того, что среднее арифметическое случайных величин отклоняется по абсолютной величине от М(Х) меньше чем на 1/2. Решение: Имеет место частный случай теоремы Чебышева. Применяя соответствующее неравенство для оценки вероятности, получим: | ||||
