|
|
ответы по терверу по 37. 1. Классификация случайных событий возможные и невозможные события, совместные и несовместные, противоположные и достоверные события. Примеры
17. Абсолютно непрерывная случайная величина. Плотность вероятности абсолютно непрерывной случайной величины, ее определение, свойства, и график.
Важный класс непрерывных случайных величин -- абсолютно непрерывные случайные величины. Это случайные величины, распределение которых имеет плотность.
Определение 3.7 Случайная величина называется абсолютно непрерывной, если существует функция такая, что
,
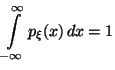 , ,
имеет место равенство: 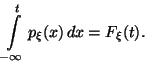
Функция , обладающая вышеперечисленными свойствами, называется плотностью распределения случайной величины .
Следствие 3.1 Если -- абсолютно непрерывная случайная величина, то
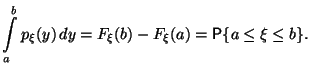
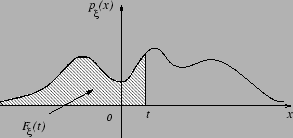
Наглядный смысл плотности можно проиллюстрировать следующим рисунком.
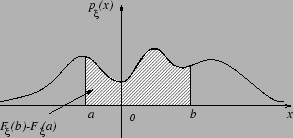
Замечание 3.5 Если плотность непрерывна в точке , то из Следствия 3.1вытекает следующее представление:
Следствие 3.2 Если -- точка непрерывности функции , то
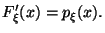
Примеры абсолютно непрерывных распределений
1) Равномерное распределение в отрезке
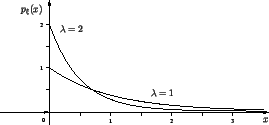
2) Показательное распределение с параметром
Показательное распределение называют также экспоненциальным.
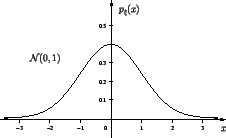
3) Нормальное (или гауссовское) распределение , , :
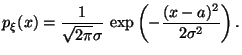
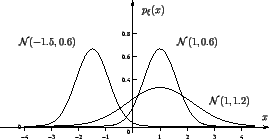
Стандартное нормальное распределение -- :
Плотность распределения удовлетворяет свойствам:
и 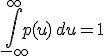 . .
И наоборот, любая интегрируемая функция , удовлетворяющая этим свойствам, может быть взята в качестве плотности распределения некоторой случайной величины.
Поскольку функция распределения является функцией верхнего предела от плотности, то последняя восстанавливается по ней дифференцированием:
.
18. математическое ожидание случайной величины и его свойства. Примеры
В некоторых случаях закон распределения случайной величины неизвестен, или просто целесообразно использовать не таблицу или функцию распределения для представления случайной величины, а так называемые числовые характеристики ее распределения, в частности математическое ожидание.
Математическое ожидание дискретной случайной величины – это сумма парных произведений всех возможных ее значений на соответствующие вероятности:
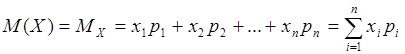 , ,
где 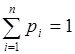 . .
Очевидно, математическое ожидание случайной величины не изменится, если таблицу значений этой случайной величины пополнить конечным числом любых чисел, считая, что вероятности этих чисел равны нулю.
Математическое ожидание 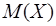 случайной величины есть величина постоянная и поэтому представляет числовую характеристику случайной величины . случайной величины есть величина постоянная и поэтому представляет числовую характеристику случайной величины .
Вероятностный смысл математического ожидания: математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.
Свойства математического ожидания можно сформулировать в виде теорем. Доказательства этих теорем будут приведены для дискретных случайных величин, однако, соответствующие теоремы справедливы также и для непрерывных случайных величин.
Прежде, чем формулировать свойства математического ожидания необходимо выяснить смысл и дать определение арифметических операций , , и т.п., где и – дискретные случайные величины.
Например, под суммой понимается случайная величина , значениями которой являются все допустимые суммы 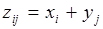 , где и – все возможные значения соответственно случайных величин и ; причем соответствующие вероятности равны: , где и – все возможные значения соответственно случайных величин и ; причем соответствующие вероятности равны:
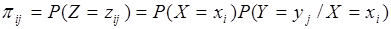 . .
Если какая-нибудь комбинация невозможна, то условно полагают ; это не отразится на математическом ожидании суммы. Аналогично определяются и остальные операции.
Свойства математического ожидания
1. Теорема. Математическое ожидание постоянной величины равно этой величине.
Доказательство. Постоянную величину можно рассматривать как случайную дискретную величину, принимающую лишь одно возможное значение с вероятностью . Поэтому 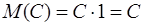 . .
2. Теорема. Математическое ожидание суммы двух (или нескольких) случайных величин и равно разности их математических ожиданий:
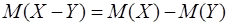
Доказательство:
1) Пусть случайная величина принимает значения с вероятностями (), а случайная величина принимает значения с вероятностями (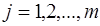 ). Тогда возможными значениями случайной величины будут суммы , вероятности которых равны: ). Тогда возможными значениями случайной величины будут суммы , вероятности которых равны:
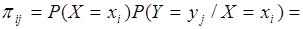
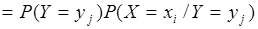 . .
Как уже отмечалось ранее, все комбинации () (, 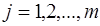 ) можно считать допустимыми, причем, если сумма невозможна, то полагаем, что . ) можно считать допустимыми, причем, если сумма невозможна, то полагаем, что .
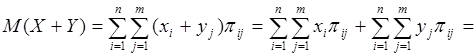
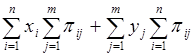
Сумма 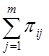 представляет собой вероятность события, состоящего в том, что случайная величина принимает значения при условии, что случайная величина примет одно из своих возможных значений (что достоверно); это сложное событие, очевидно, эквивалентно тому, что принимает значение и поэтому представляет собой вероятность события, состоящего в том, что случайная величина принимает значения при условии, что случайная величина примет одно из своих возможных значений (что достоверно); это сложное событие, очевидно, эквивалентно тому, что принимает значение и поэтому 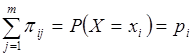 . .
Аналогично 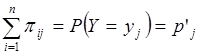 . .
Тогда 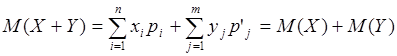 . .
2) Для нескольких случайных величин, например для трех , и , имеем:
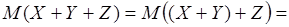
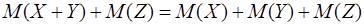 , и т.д. , и т.д.
Следствие. Если – постоянная величина, то: 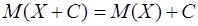
3. Теорема. Математическое ожидание произведения двух независимых случайных величин и равно произведению их математических ожиданий:
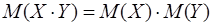
Доказательство. Пусть случайная величина принимает значения (,) () и (,) ( ) – законы распределения случайных величин и . Так как и – независимы, то полный набор значений случайной величины состоит из всех произведений (, ) – законы распределения случайных величин и . Так как и – независимы, то полный набор значений случайной величины состоит из всех произведений (,  ), причем вероятности этих значений по теореме умножения для независимых событий равны . ), причем вероятности этих значений по теореме умножения для независимых событий равны .
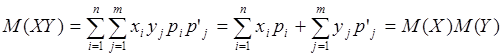
Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин.
Действительно, например, для трех взаимно независимых случайных величин , и :
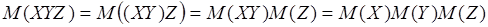 , и т.д. , и т.д.
Следствие. Постоянный множитель можно выносить за знак математического ожидания, т.е.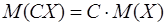 . .
Если – постоянная величина и – любая случайная величина, то, учитывая, что и – независимы, получим:
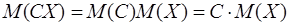 . .
Следствие. Математическое ожидание разности двух случайных величин и равно разности их математических ожиданий: 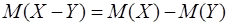 . .
Доказательство. 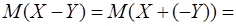
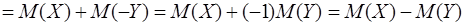 . .
Примеры
Пусть случайная величина имеет дискретное равномерное распределение, то есть 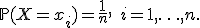 Тогда её математическое ожидание Тогда её математическое ожидание
![m[x] = \frac{1}{n} \sum\limits_{i=1}^n x_i](5037_html_m17811b70.gif)
равно среднему арифметическому всех принимаемых значений.
Пусть случайная величина имеет непрерывное равномерное распределение на интервале , где . Тогда её плотность имеет вид ![f_x(x) = \frac{1}{b-a} \mathbf{1}_{[a,b]}(x)](5037_html_m13f3c3a9.gif) и математическое ожидание равно и математическое ожидание равно
![m[x] = \int\limits_{a}^b\!\frac{x}{b-a}\, dx = \frac{a+b}{2}](5037_html_m4f6436d2.gif) . .
Пусть случайная величина имеет стандартное распределение Коши. Тогда
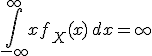 , ,
то есть математическое ожидание не определено.
19. Дисперсия случайной величины и ее свойства. Среднее квадратическое отклонение случайной величины. Примеры.
1. Дискретная случайная величина, закон и функция распределения
Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Например, денежный выигрыш в какой-нибудь лотерее, или количество очков при бросании игральной кости, или число появления события при нескольких испытаниях. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счётным множеством)
Для сравнения - непрерывная случайная величина может принимать любые значения из некоторого числового промежутка: например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д.
Закон распределения дискретной случайной величины представляет собой перечень всех её возможных значений и соответствующих вероятностей. Сумма всех вероятностей Σpi = 1. Закон распределения также может быть задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (xi; pi)
Функция распределения случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x:
F(X) = P(ξ < X).
Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины. Ниже будет приведён пример, разъясняющий смысл сказанного.
2. Числовые характеристики дискретных случайных величин
Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности:
M(X) = x1p1 + x2p2 + ... + xnpn
Свойства математического ожидания.
1) Математическое ожидание постоянной величины равно самой величине:
М(С) = С
2) Постоянный множитель можно выносить за знак математического ожидания:
М(СХ) = С·М(Х)
3) Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
М(Х1 + Х2 + …+ Хn) = М(Х1) + М(Х2) + ... + М(Хn)
4) Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
М(Х1 · Х2 · ... · Хn) = М(Х1) · М(Х2) · ... · М(Хn)
Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания:
D(X) = (x1 - M(X))2p1 + (x2 - M(X))2p2 + ... + (xn- M(X))2pn = x21p1 + x22p2 + ... + x2npn - [M(X)]2
Свойства дисперсии.
1) Дисперсия постоянной величины равна нулю: D(С) = 0
2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С2· D(Х)
3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х1 ± Х2 ± ... ± Хn) = D(Х1) + D(Х2) + ... + D(Хn)
Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии:
σ(X) = √D(X)
Мода дискретной случайной величины Mo(X) - это значение случайной величины, имеющее наибольшую вероятность. На многоугольнике распределения мода - это абсцисса самой высокой точки. Бывает, что распределение имеет не одну моду.
Коэффициент вариации случайной величины - это относительная мера вариации.
V(X) = |σ(X)/M(X)| · 100%
Асимметрия (коэффициент асимметрии) случайной величины (и дискретной, и непрерывной) As(X) - величина, характеризующая степень асимметрии распределения относительно математического ожидания. Коэффициент асимметрии дискретной случайной величины вычисляется по формуле:
As(X) = [(x1-M(X))3p1 + (x2-M(X))3p2 + ... + (xn-M(X))3pn]/σ3
Если коэффициент асимметрии отрицателен, то либо большая часть значений случайной величины, либо мода находятся левее математического ожидания, и наоборот, если As(X)>0, то правее.
Эксцесс (коэффициент эксцесса) случайной величины (и дискретной, и непрерывной) Ex(X) - величина, характеризующая степень островершинности или плосковершинности распределения, т.е. степень так называемого «выпада». Коэффициент эксцесса дискретной случайной величины вычисляется по формуле:
Ex(X) = [(x1-M(X))4p1 + (x2-M(X))4p2 + ... + (xn-M(X))4pn]/σ4 - 3
|
|
|
 Скачать 4.53 Mb.
Скачать 4.53 Mb.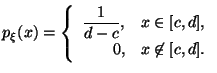
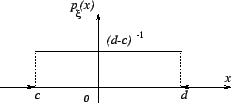
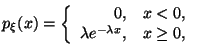

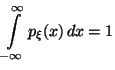 ,
,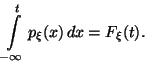

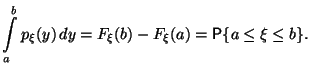

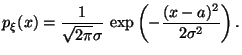

 .
.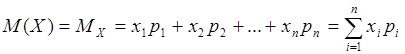 ,
,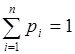 .
.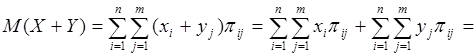
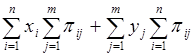
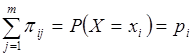 .
.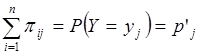 .
.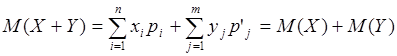 .
.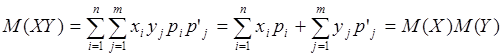
![m[x] = \int\limits_{a}^b\!\frac{x}{b-a}\, dx = \frac{a+b}{2}](5037_html_m4f6436d2.gif) .
. 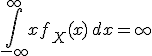 ,
,