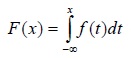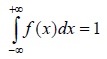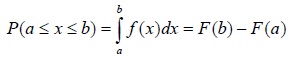ответы по терверу по 37. 1. Классификация случайных событий возможные и невозможные события, совместные и несовместные, противоположные и достоверные события. Примеры

• Название: 1. Классификация случайных событий возможные и невозможные события, совместные и несовместные, противоположные и достоверные события. Примеры
• Анкор: ответы по терверу по 37.docx
• Дата: 22.04.2017
• Размер: 4.53 Mb.
• Имя файла: ответы по терверу по 37.docx
• Тип: Документы; #5037
• страница: 2 из 6

Системы дискретных случайных величин

До сих пор мы рассматривали случайные величины изолированно друг от друга, не касаясь вопроса об их взаимоотношениях. Однако в практических задачах часто встречаются ситуации, когда те или иные случайные величины приходится изучать совместно. В таких случаях говорят о системе нескольких случайных величин. Более точно: случайные величины образуют систему, если они определены на одном и том же пространстве элементарных событий .

Систему двух случайных величин (X, Y) можно истолковывать как случайную точку на плоскости, систему трех случайных величин (X, Y, Z) – как случайную точку в трехмерном пространстве. Мы ограничимся в основном двумерным случаем.

Интуитивный подход к понятию системы двух случайных величин связан с представлением об опыте, результатом которого является пара чисел X, Y. Поскольку исход опыта мыслится как случайное событие, то предсказать заранее значения чисел X и Y невозможно (при повторении опыта они меняются непредвиденным образом). Приведем несколько примеров.

Пример 1. Дважды бросается игральная кость. Обозначим через X число очков при первом бросании, через Y– число очков во втором. Пара (X, Y) будет системой двух случайных величин.

Пример 2. Из некоторой аудитории наугад выбирается один студент; X – его рост (скажем, в

сантиметрах), Y – вес (в килограммах).

Пример 3. В данном сельскохозяйственном районе выбирается произвольно участок посева пшеницы площадью 1 га; X – количество внесенных на этом участке удобрений, Y – урожай, полученный с участка.

Пример 4. Сравниваются письменные работы по математике и русскому языку; X– оценка за работу по математике, Y – за работу по русскому языку.

Список подобных примеров легко продолжить.

Определение независимости случайных величин.

Пусть задана система (X, Y). Мы скажем, что величины X и Y независимы, если независимысобытияX АиY В, гдеАиВ– любыедваотрезка[a₁, a₂] и[b₁, b₂].

Иными словами выполняется равенство

PX  A, Y B  PX  A PY B.

13.* Математические операции над дискретными случайными величинами. Примеры.
Если случайная величина может принимать конечное или счетное множество значений, то она называется дискретной (дискретно распределенной).
1. «Сдвиг». Пусть имеется дискретная СВ Х, принимающая в зависимости от результата тесты те либо другие случайные значения. Ежели к каждому из этих значений прибавить одно и то же число, к примеру, А, то в итоге получим новейшую СВ - Х + А, принимающую значения (  , При всем этом:

 , т.е. с теми же вероятностями, что и СВ Х.

Х	х1	…	хn
Р	р1	…	рn

Х + А	х1 + А	…	хn + А
Р	р1	…	pn

2. Определение. Произведением дискретной СВ на число с именуется дискретная СВ сХ, принимающая значения  с вероятностями  .

3. «Возведение в степень».

Определение. Квадратом (соответственно – m-степенью) дискретной СВ Х именуется дискретная СВ, принимающая значения  (соответственно -  ) с вероятностями  . Обозначение – Х² (соответственно – X^m).

Построение таблицы значений СВ Х² несколько труднее. Разглядим определенный пример.

Задачка. СВ Х задана таблицей распределения. Найти закон распределения СВ Х².

Х	-1
Р	0,2	0,3	0,4	0,1

Решение. Действуем аналогичным методом для вычисления Х², т.е. заменяем все значения х_i значениями их квадратов - х_i², и получаем:

Х2
Р	0,2	0,3	0,4	0,1

В первой строке имеются совпадающие значения. Потому следует объединить их в одну варианту, сложив надлежащие вероятности.

Х2
Р	0,6	0,3	0,1

Таблицу распределения хоть какой СВ У = f(x) для хоть какой функции f можно выстроить аналогично. Она строится в два шага. Поначалу рассчитываются элементы вспомогательной таблицы.

СВ	f(x1)	f(x2)	…	f(xn)
Р	p1	p2	…	pn

Потом совпадающие значения f(x_i) = f(x_j) для различных значений x_i и x_j (ежели такие имеются) объединяются в одно, а надлежащие вероятности складываются.

4. Определение. Суммой дискретной СВ Х, принимающей значения  с вероятностями  и СВ Y, принимающей значения  с вероятностями именуется дискретная СВ Z = Х + Y, принимающая значения  с вероятностями  для всех указанных значений i и j.

5. Определение. Разностью дискретной СВ Х, принимающей значения  с вероятностями  и СВ Y, принимающей значения  с вероятностями  именуется дискретная СВ Z = Х - Y, принимающая значения  с вероятностями  для всех указанных значений i и j.

6. Определение. Произведением дискретной СВ Х, принимающей значения  с вероятностями  и СВ Y, принимающей значения  с вероятностями  именуется дискретная СВ Z = Х·Y, принимающая значения  с вероятностями  для всех указанных значений i и j.

14. Функция распределения случайной величины, ее определение, свойства и график. Примеры.

Числовая величина, принимающая то или иное значение в результате реализации испытания случайным образом, называется случайной величиной.

Если x - дискретная случайная величина, принимающая значения x1 < x2 < … < xi < … с вероятностями p1 < p2 < … < pi < …, то таблица вида

x1	x2	…	xi	…
p1	p2	…	pi	…

называется распределением дискретной случайной величины.

Функция распределения случайной величины, с таким распределением, имеет вид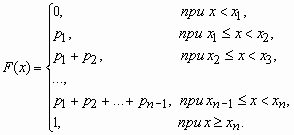



Свойства функции распределения.

1. .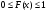

Доказательство: Это утверждение следует из того, что функция распределения – это вероятность, а как известно,.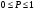

2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси.

Доказательство: Пусть х₁2. Докажем, что F(x₁)F(x₂). Пусть событие А=(Х1), B=(x₁Х2). Тогда А+В=(Х2). События А и В несовместны, следовательно по теореме сложения Р(А+В)=P(А)+P(В). То есть Р(Х2) =Р(Х1)+Р(x₁Х2). Другими словами F(x₂)=F(x₁)+ Р(x₁Х2). (3)

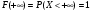Так как Р(x₁Х2) как вероятность невозможного события Х. как вероятность достовероного события Х.

4. Р(х₁Х2)=F(x₂)-F(x₁). (4)

Доказательство: это непосредственно следует из формулы (3).

Пример: 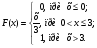Найти вероятность того, что случайная величина Х примет значение в интервале [2; 5).

Решение: По формуле Р(х₁Х2)=F(x₂)-F(x₁). (4)

Р(2Х<5)=F(5)-F(2)=1-2/3=1/3. (4).

Ответ : 1/3.

15. Функция распределения дискретной случайной величины. Примеры.

если  - дискретная случайная величина, принимающая значения x₁ < x₂ < … < x_i < … с вероятностями p₁ < p₂ < … < p_i < …, то таблица вида

x1	x2	…	xi	…
p1	p2	…	pi	…

называется распределением дискретной случайной величины.

Функция распределения случайной величины, с таким распределением, имеет вид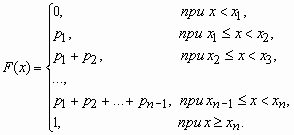



У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:

1	2	3	4	5	6
1/6	1/6	1/6	1/6	1/6	1/6

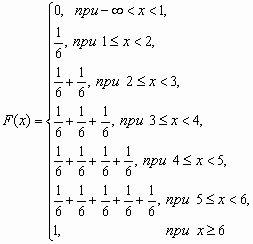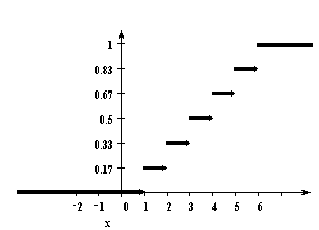16. Теорема о существовании случайной величины с заданной функцией распределения. Непрерывная случайная величина. Вероятность отдельно взятого значения непрерывной случайной величины. Примеры.

Как известно, случайной величиной называется переменная величина, которая может принимать те или иные значения в зависимости от случая. Случайные величины обозначают заглавными буквами латинского алфавита (X, Y, Z), а их значения – соответствующими строчными буквами (x, y, z). различают непрерывные и дискретные случайные величины.

Непрерывной случайной величиной называется случайная величина Х, если ее функция распределения (интегральная функция распределения) представима в виде:

где f(x) – некоторая неотрицательная функция, такая что

Функция f(x) называется плотностью распределения вероятностей случайной величины X (дифференциальной функцией распределения).

Вероятность того, что непрерывная случайная величина X принимает значение в заданном промежутке, вычисляется следующим образом:

Примеры распределений вероятностей непрерывной случайной величины Х:

• 
  равномерное распределение вероятностей непрерывной случайной величины;
  
• 
  показательное распределение вероятностей непрерывной случайной величины;
  
• 
  нормальное распределение вероятностей непрерывной случайной величины.