билеты прикладной математике за 1 семестр. 1. Случайные события, их классификация. Понятие вероятности
 Скачать 120 Kb. Скачать 120 Kb.
|
|
1. Случайные события, их классификация. Понятие вероятности. Случайное событие – любой исход, который может произойти, либо не произойти в результате проводимых испытаний. Два события несовместны, если наступление одного из них исключает наступление другого. Следовательно, совместны те события, которые не исключают наступление одного при наступлении другого, т.е. они могут наступить вместе. Теория вероятностей изучает свойства случайных массовых событий, которые могут многократно повторяться при воспроизведении определенного комплекса условий. Основные понятия теории вероятностей были заложены в 15-17 вв. паскалем и др. Эти понятия зародились в результате попыток математически описать азартные игры. 2. Алгебра случайных событий, диаграммы Вьенна-Эйлера. Лекции стр. 8 3. Классическое определение вероятности. Комбинаторика. Р(А) = n(A)/n(Ω) – классическое определение вероятности. n(A) – количество исследуемых испытаний; n(Ω) – количество произведенных испытаний. Задачи, в которых необходимо подсчитывать число возможных способов совершения каких-либо действий называются комбинаторными, а раздел математики, занимающийся решением таких зада, - комбинаторикой. 4. Аксиоматическое построение теории вероятностей. Аксиоматическое вероятность задается числовой функцией в соответствии с 3 аксиомами: Определение: Вероятностью называется числовая функция, определенная, определенная на поле событий S и обладающая следующими свойствами: Аксиома 1. Для любого события А€S P(A)>=0. Аксиома 2. Вероятность достоверного события равна единице P(Ω) = 1/ Аксиома 3. Вероятность объединения двух несовместных событий равна сумме вероятностей этих событий: А€S, В€S, А∩ В=○, P(AB)=P(A)+P(B) 5. Теоремы о вероятности суммы событий. Если события А и В не совместны, то А+В=Р(А)+Р(В) Если события А и В совместны, то А+В = АВ + АВ +АВ Для совместных и несовместных событий Р(А+В) = Р(А) + Р(В) – Р(АВ) 6. Условная вероятность. Зависимые и независимые события. Теоремы о вероятности произведения событий. Р(А/В) – вероятность А при условии В (достоверное событие) – называют условной вероятностью. Событие А называют независимым, от события В, если появление (или не появление) события В не изменяет вероятности появления события А. Событие А называется зависимым от события В, если появление (или не появление) события В изменяет вероятность появления события А. Теорема умножения вероятностей: Р(АВ) = Р(А/В) * Р(В) = Р(В/А) * Р(А) Теорема умножения независимых событий: Р(АВ) = Р(А) *Р(В) 7. Формула полной вероятности. Если события Н1, Н2,….,Нn образуют полную группу, то для вычисления вероятности произвольного события А применяется формула полной вероятности Р(А) = ∑ Р(Н) * Р(А/Нi) В соответствии с которой вероятность наступления события А может быть представлена как сумма произведений условных вероятностей события А при условии наступления событий Нi на безусловные вероятности этих событий Нi. Поскольку среди событий Н1, Н2,…,Нn, образующих полную группу, в результате опыта должно наступить одно и только одно событие, эти события Нi называют гипотезами. 8. Формула Байеса. РА(Вi) = Р(Вi) * РВi(A)/Р(А), где Р(А) = ∑ Р(Н) * Р(А/Нi) – формула полной вероятности. 9. Схема Бернулли. Формула Бернулли. Наивероятнейшее число успехов. Пусть проводится конечное число n последовательных испытаний, в каждом из которых некоторое событие А может либо наступить (успех), либо не наступить (неудача), причем эти испытания удовлетворяют следующим условиям:
Такая последовательность испытаний называется схемой Бернулли или биноминальной схемой, а сами испытания – испытаниями Бернулли. Для расчета вероятности Рn(к) того, что в серии из n испытаний Бернулли окажется ровно k успешных, применяется формула Бернулли Рn(k) = Cnk * pk * (1-p)n-k (k = 0,1,2,…n). 10. Понятие случайной величины. Дискретная случайная величина, способы ее задания: ряд распределения. Х – случайная величина, которая принимает в каждом опыте одно значение из множества, которое заранее предугадать нельзя. Случайная величина является числовой функцией (или вектором), определенной на пространстве элементарных событий Ω. Случайная величина называется дискретной, если множество конечных значений конечно или счетно. Законом распределения случайной величины называется любое соотношение, связывающее возможные значения этой случайной величины и соответствующие им вероятности. Закон распределения дискретной случайной величины Х определен, если известны все Хn и вероятности Рn = Р(Х=Хn) такие, что Р1 + Р2 + Р3 + … = 1. Если составить таблицу, в верхней строке которой поместить значения дискретной случайной величины, а в нижней – соответствующие вероятности, то получим ряд распределения случайной величины. Сумма вероятностей записанных во второй строке должна быть равна 1. Еще случайную дискретную величину можно задать и многоугольником распределения. Многоугольником дискретной случайной Х величины называется ломаная, соединяющая точки (хi;pi), расположенные в порядке возрастания. 11. Функция распределения дискретной случайной величины и ее свойства. Функцией распределения случайной величины Х называется функция FX(x) = P(X<x), x € R. Под (X<x) понимается событие, состоящее в том, что случайная величина Х примет значение, меньшее, чем число х. Если известно, о какой случайной величине идет речь, то индекс, обозначающий эту случайную величину, опускается: FX(x) = F(x). Свойства: для любого x€ R: 0<= F(x) <=1; F(-∞) = lim F(x)=0; F(+∞) = lim F(x)=1; F(x) является неубывающей функцией, т.е. для любых х1,х2 € R, таких, что х1<х2: F(x1) <=F(x2); F(x) непрерывна слева, т.е. для любого x€ R: F(x) = F(x-0) = lim F(z). 12. Математическое ожидание дискретной случайной величины и ее свойства. Математическое ожидание дискретной случайной величины Х называется взвешенная сумма всех ее значений, где в значении веса выступает вероятность М(Х) = ∑ Хi Рi Свойства:
13. Дисперсия дискретной случайной величины и ее свойства. Дисперсия случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания D(X) = M(X-MX)2 или D(X) = M(X2) – (M(X))2 Свойства:
Средним квадратичным отклонением Х называется неотрицательное значение квадратного корня из дисперсии: σх = +√D(X) 14. Биноминальный закон распределения: ряд распределения и основные числовые характеристики. Случайная величина Х называется распределенной по биноминальному закону с параметрами n,p (где n € R, p € [0,1]), если она принимает значения 0, 1, 2,…,n с вероятностями P(X=x) = Cnxpx(1-p)n-x (x = 0,1,2,…,n). Ряд распределения случайной величины Х имеет следующий вид:
15. Геометрический закон распределения. Случайная величина Х называется распределенной по геометрическому закону распределения с параметром р (где р € [0,1]), если она принимает значения 1,2,3,… с вероятностями Р(Х=х) = р(1-р)х-1 (х=1,2,3,…). Математическое ожидание случайной величины, имеющей геометрической распределение равно М(Х) = 1/р, а ее дисперсия D(Х) = 1-р/р2. 16. Пуассоновский закон распределения: ряд распределения и основные числовые характеристики. Случайная величина Х называется распределенной по закону Пуассона с параметром λ (где λ >= 0), если она принимает значения 0,1,2… с вероятностями Р(Х=х) = (λх/х!)*е-λ (х=0,1,2,…) Математическое ожидание случайной величины Х, распределенной по закону Пуассона, совпадает с ее дисперсией и равно параметру λ: М(Х)=D(Х)=λ. 17. Непрерывная случайная величина. Функция распределения и функция плотности вероятности, их свойства. Случайная величина Х называется непрерывной, если она примет более чем счетное число значений. fx(x) называется плотностью распределения случайной величины Х. График плотности распределении случайной величины Х называется кривой распределения случайной величины. Если известно, о какой случайной величине идет речь, индекс, обозначающий эту случайную величину, опускается f(x) = fx(x). Свойства плотности распределения: для всех х € R: f(x)>=0; ∫f(z)dz = 1; для всех точек х € R, в которых существует производная F’(x). Вероятность того, что непрерывная случайная величина Х примет конкретное число значения, равна нулю: для всех х € R: Р(Х=х) = 0. Вероятность попадания непрерывной случайной величины в числовой промежуток можно рассчитать по следующим формулам: для всех с, d € R: таких, что с Р(с<=X<=d) = P(c<=X<=d) = P(c<=X<=d) = P(c Математическое ожидание непрерывной случайной величины называется число М(Х) = ∫хf(x)dx. Две случайные величины (произвольные, непрерывные или дискретные) Х и Y называются независимыми, если для всех х,y € R P[(X Т.е. если для всех х,y € R события (Х Свойства:
Дисперсия случайной величины: D(X)=∫(x-M(x)2f(x)dx, D(x)=∫x2f(x)dx-(M(x))2 Свойства:
19. Начальные и центральные моменты. Начальным моментом порядка k случайной величины Х называют математическое ожидание величины Хk: vk=M(Xk). В частности, начальный момент первого порядка равен математическому ожиданию: v1 = M(x). Центральным моментом порядка k случайной величины Х называют математическое ожидание величины (Х-М(Х))k: μk = М(Х-М(Х))=0; В частности, центральный момент первого порядка равен 0: μ1 = М(Х-М(Х))=0; центральный момент второго порядка равен дисперсии: μ2 = М(Х – М(Х))2 = D(X). Центральные моменты целесообразно вычислять, используя формулы, выражающие центральные моменты через начальные: μ2 = v2-v12, μ3 = v3 – 3v1v2 +2v13, μ4=v4-4v1v3+6v12v2-3v14. 20. Равномерный закон распределения: плотность и функция распределения, основные числовые характеристики. Например минутная стрелка остановившихся механических часов будет показывать какое-то значение; заранее, до поломки, неизвестно, какое именно, но точно известно, что оно будет в пределах от 0 до 60. Погрешность округления также относится к подобным величинам. О таких величинах говорят, что они распределены по равномерному закону на некотором отрезке [a,b]. Более строго, случайная величина Х с функцией распределения Называется распределенной по равномерному закону на отрезке [a,b]. Плотность распределения получается путем дифференцирования: Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством: М(Х) = ∫xf(x) dx Где f(x) – плотность распределения случайной величины Х. Модой М0(Х) непрерывной случайной величины Х называют ее возможное значение, которому соответствует локальный максимум плотности распределения. В частности, если распределение имеет два одинаковых максимума, то его называют бимодальным. Медианой Ме(Х) непрерывной случайной величины Х называют то ее значение, которое определяется равенством Р[X Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством D(X) = ∫[x-M(X)]2f(x) dx или D(X) = ∫x2f(x) dx – [M(X)]2 Среднее квадратичное отклонение непрерывной случайной величины определяется σ(Х) = √D(X) 21. Показательный закон распределения: плотность и функция распределения, основные числовые характеристики. Показательным называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью 0 при x<0, 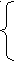 f(x) = f(x) = λe-λx при x>=0 где λ – постоянная положительная величина. Функция распределения показательного закона 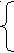 0 при x<0 0 при x<0F(x) = 1-е-λх при x>=0 Вероятность попадания в интервал (a,b) непрерывной случайной величины Х, распределенной по показательному закону, P(a Математическое ожидание - М(Х) = 1/μ. Дисперсия - D(X) = 1/μ2 22. Поток событий. Простейший поток. Распределение промежутка времени между последовательными событиями простейшего потока. Свойство марковости показательного закона. 24. Нормальный закон распределения: функция плотности и функция распределения, основные числовые характеристики. Нормальным называют распределение вероятностей непрерывной случайной величины Х, плотность которого имеет вид F(x) = (1/σ√2π) * e-(x-a)2//(2σ2) Где a – математическое ожидание, σ – среднее квадратичное отклонение Х. Вероятность того, что Х примет значение, принадлежащее интервалу (α, β), P(α Где Ф(х) = 1/√2π∫е-х2/2dx – функция Лапласа. Вероятность того, что абсолютная величина отклонения меньше положительно числа δ, Р(!X-a! <δ) = 2Ф(δ/σ). 25. Функция Лапласа и ее свойства. Вероятность попадания нормально распределенной случайной величины в заданный интервал. Правило «трех сигм». 26. Неравенство Чебышева. Понятие о законе больших чисел. Теорема Чебышева ( без док-ва). Теорема Бернулли (без док-ва). Неравенство Чебышева: Если случайная величина Х имеет конечное математическое ожидание М(Х) и дисперсию D(Х) , то для любого ε>0 справедливо равенство P{|X – M(X) | <=ε} > 1-D(X)/ε2 Под законом больших чисел понимается обобщенное название группы теорем, утверждающих, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным. Теорема Чебышева: Если дисперсии независимых случайных величин Х1,Х2,…,Хn ограничены сверху числом В, то для произвольного, сколь угодно малого ε>0 справедливы неравенство Р{|∑Xi/n - ∑M(Xi)/n| <=ε}> 1 – B/nε2 и предельное равенство limP{|∑Xi/n - ∑M(Xi)/n| <=ε} = 1 Теорема Бернулли: Если вероятность успеха в каждом n независимых испытаний постоянна и равна p, то для произвольного, сколь угодно малого ε>0 справедливо равенство limP{|m/n -p|<=ε}=1, где m – число успехов в серии из n испытаний. 27. Центральная предельная теорема ( без док-ва). Локальная и интегральная теоремы Муавра-Лапласа. Центральная предельная теорема: Пусть Х1,Х2,…,Хn – независимые случайные величины, имеющие конечный третий абсолютный момент (дисперсию σ2). Положим ai = M(Xi), σi2 = D(Xi), Ci3 = M|Xi-ai|3, i=1,2,3,.... Тогда если То при n→∞ для x(-∞ Локальная теорема Муавра-Лапласа. Если вероятность р успеха в каждом испытании отлична от 0 и 1, а число испытаний n достаточно велико, то для расчета Рn(k) можно пользоваться приближенной формулой Рn(k) = (1/√np(1-p)) * φ(u) (k=0,1,2,...), Где φ(u)=(1/√2π) * e-u2/2, u=k-np/√np(1-p) Интегральная теорема Муавра-Лапласа. Если вероятность р успеха в каждом испытании отлична от 0 и 1, а число испытание n достаточно велико, то для расчета вероятности Рn(k1,k2) того, что число успехов в серии из n испытаний будет заключено в промежутке [k1,k2), можно пользоваться приближенной формулой Рn(k1,k2) = Ф0(u2) – Ф0(u1) (k1 = 0,1,2,..; k2>k1), где Ф0(u) = (1/√2π) * ∫е-z2/2dz, u1,2 = k1,2 – np/√np(1-p) 28. Двумерные случайные величины, формы задания закона распределения. Двумерной называют случайную величину (X,Y), возможные значения которой есть пары чисел (x,y). Дискретной называют двумерную величину, составляющие которой дискретны. Непрерывной называют двумерную величину, составляющие которой непрерывны. Законом распределения вероятностей двумерной случайной величины называют соответствие между возможными значениями и их вероятностями. Закон распределения дискретной двумерной случайной величины может быть задан:
Функцией распределения вероятностей двумерной случайной величины называют функцию F(x,y), определяющую для каждой пары чисел (x,y) вероятность того, что Х примет значение, меньшее х, и при этом Y примет значение меньшее y: F(x,y) = P(X Зная плотность распределения составляющих X и Y непрерывной двумерной случайной величины (X,Y), можно найти их математическое ожидание и дисперсии: M(X) = ∫xf1(x) dx, M(Y) = ∫yf2(y) dy; D(X) = ∫[x-M(X)]2f1(x) dx = ∫x2f1(x) dx – [M(X)]2; D(Y) = ∫[y-M(Y)]2f2(y) dy = ∫y2f2(y) dy – [M(Y)]2. 30. Зависимость случайных величин. Корреляционный момент и коэффициент корреляции, их свойства. Степень зависимости случайных величин измеряется с помощью ковариации случайных величин X и Y: cov(X,Y) = M(XY) – M(X)*M(Y) Ковариация может принимать произвольные вещественные значения, поэтому не вполне пригодна к использованию в качестве меры связи случайных величин. В этом смысле более пригоден коэффициент корреляции случайных величин Х и Y ρ(Х,Y) = M(XY) – M(X)*M(Y)/σxσy Если коэффициент корреляции ρ(Х,Y)=0, то это не обязательно означает независимость случайных величин Х и Y. В этом случае говорят, что данные случайные величины некоррелированны. Коррелированными называют две случайные величины, если их корреляционный момент отличен от нуля. Корреляционным моментом μ1,1 порядка 1+1: μxy = М{[X – M(X)] * {Y-M(Y)]} 31. Предмет математической статистики. Генеральная совокупность, выборка, ее свойства. Основная задача математической статистики состоит в получении выводов о массовых явлениях и процессах по данным наблюдений над ними или экспериментов. Генеральной совокупностью называют совокупность результатов всех мысленно возможных наблюдений за какой-либо случайной величиной Х, проводимых в одинаковых условиях. Иными словами, генеральная совокупность представляет собой набор всех возможных значений данной случайной величины. Выборкой называют результаты ограниченного числа наблюдений за случайной величиной Х. Сущность выборочного метода состоит в том, чтобы по выборке как некоторой части генеральной совокупности делать выводы о генеральной совокупности в целом. Выборку называют репрезентативной, если она адекватно отражает исследуемые свойства генеральной совокупности. Чтобы выборка была репрезентативной, можно организовать ее следующим способом. Из генеральной совокупности случайным образом отбирается элемент, затем он обследуется, после чего возвращается в общую совокупность и может быть отобран и обследован повторно. Такая выборка называется повторной случайной. Конкретной выборкой называется конкретный набор чисел х1,х2,…,хn, полученный в результате наблюдений за случайной величиной Х, т.е. набор, состоящий из n реализаций случайной величины Х. Выборочным средним называется: Х = ∑Хi/n 32. Статистический и интервальный ряды распределения. Расположив элементы выборки в порядке не убывания, получим вариационный ряд х1,х2,…,хn. Если в вариационном ряду есть повторяющиеся элементы, то выборку можно записать в виде статистического ряда распределения, т.е. в виде таблицы:
Для непрерывных случайных величин при достаточно больших объемах выборки n вместо статистического ряда распределения используют интервальный вариационный ряд,
Где v – число интервалов одинаковой ширины h=хn-x1/1+3,322lg n (x1 и хn – соответственно минимальный и максимальный элементы выборки; значение h рассчитывается с числом знаков после запятой, на единицу большим, чем в исходных данных). 33. Выборочные аналоги функции распределения и функции плотности. Полигон, гистограмма, кумулята. Выборочным аналогом плотности распределения fx(x) случайной величины Х служит выборочная плотность распределения f^x(x) = p^i/h при х €[ai; ai+1) (i = 1,2,...,v). Полигоном частот называют ломаную, отрезки которой соединяют точки (х1,n1), (x2,n2),...,(xk,nk), где xi – варианты выборки и ni – соответствующие им частоты. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношения ni/h (плотность частоты) 34. Распределения χ2, T, F. 35. Свойства точечных оценок числовых характеристик и параметров распределения. Статистической оценкой Θ* неизвестного параметра Θ теоретического распределения называют функцию f(Х1,Х2...,Хn) от наблюдаемых случайных величин Х1,Х2,…,Хn . Точечной называют статистическую оценку, которая определяется одним числом Θ* = f(x1,x2,...,xn), где х1,х2,…,хn – результаты n наблюдений над количественным признаком Х (выборка). Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при лбом объеме выборки. Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру. Несмещенной оценкой генеральной средней служит выборочная средняя Хв = (∑nixi)/n Где xi – вариант выборки, ni – частота варианты xi, n = ∑ni – объем выборки. 36. Точечная оценка математического ожидания и ее свойства. Несмещенная оценка математического ожидания М(Х) Х = ∑Хi/n 37. Точечная оценка дисперсии, несмещенная оценка дисперсии. Смещенной оценкой генеральной дисперсии служит выборочная дисперсия Dв = (∑ni(xi-xв)2)/n; Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия S2X = (∑nixi2 – [∑niui]2/n)/n-1 38. Метод моментов. Метод максимального правдоподобия. Методом моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка. Если распределение определяется одним параметром, то для его отыскания приравнивают один теоретический момент одному эмпирическому моменту того же порядка. Если распределение определяется двумя параметрами, то приравнивают два теоретических момента двум соответствующим эмпирическим моментам того же порядка. Метод наибольшего правдоподобия точечной оценки известных параметров заданного распределения сводится к отысканию максимума функции одного или нескольких оцениваемых параметров. 39. Интервальные оценки параметров распределения. Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр. |
