билет. билеты эвм. 1. Комплексные числа. Комплексное число
 Скачать 1.65 Mb.
|
|
1.Комплексные числа. Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел. Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i2 = –1). Число  = a – bi называется комплексно-сопряженным к z = a + bi. Равенство z · = a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число: .(Например, 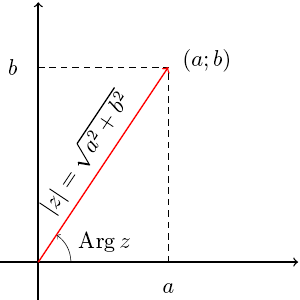 .) У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a; b) равна  . Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом комплексного числа z и обозначается Arg z. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор. Но если вектор длины r образует угол φ с положительным направлением оси абсцисс, то его координаты равны (r · cos φ; r · sin φ). Отсюда получается тригонометрическая форма записи комплексного числа: z = |z| · (cos(Arg z) + i sin(Arg z)). Часто бывает удобно записывать комплексные числа именно в такой форме, потому что это сильно упрощает выкладки. Умножение комплексных чисел в тригонометрической форме выглядит очень просто: z1 · z2 = |z1| · |z2| · (cos(Arg z1 + Arg z2) + i sin(Arg z1 + Arg z2)) (при умножении двух комплексных чисел их модули перемножаются, а аргументы складываются). Отсюда следуют формулы Муавра: zn = |z|n · (cos(n · (Arg z)) + i sin(n · (Arg z))). С помощью этих формул легко научиться извлекать корни любой степени  из комплексных чисел. Корень n-й степени из числа z — это такое комплексное число w, что wn = z. Видно, что  , а  , где k может принимать любое значение из множества {0, 1, ..., n – 1}. Это означает, что всегда есть ровно n корней n-й степени из комплексного числа (на плоскости они располагаются в вершинах правильного n-угольника).2.Числовая последовательности. Предел функции, свойства пределов. Числовая последовательность представляет собой не что иное, как множество нумерованных чисел, упорядоченных наподобие натурального ряда, т.е. располагаемое в порядке возрастания номеров. Последовательность может содержать как конечное, так и бесконечное число членов. Последовательность, состоящая из конечного числа членов, называется конечной, а последовательность, состоящая из бесконечного числа членов, - бесконечной последовательностью.    3. Замечательные приделы. Раскрытие неопределённости.    Раскрытие неопределённостей Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:
по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют. Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих. Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки. Для раскрытия неопределённостей видов  ,  ,  пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.   Для раскрытия неопределённостей типа  используется следующий алгоритм:Выявление старшей степени переменной; Деление на эту переменную как числителя, так и знаменателя. Для раскрытия неопределённостей типа  существует следующий алгоритм:Разложение на множители числителя и знаменателя; Сокращение дроби. Для раскрытия неопределённостей типа 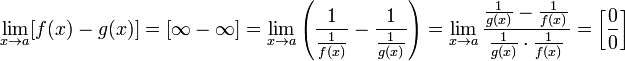 иногда удобно применить следующее преобразование:Пусть  и   Пример «Замечательный предел»  — пример неопределённости вида 0 / 0. По правилу Лопиталя 4.Производная. Деферинциалы высших порядков. Производная функции – отношение приращения функции к приращению аргумента при бесконечно малом приращении аргумента: f′(x)=ΔfΔx при Δx→0 Базовые производные c′=0(xa)′=a⋅xa−1 (a∈R)(sinx)′=cosx(cosx)′=−sinx Правила дифференцирования Константа выносится за знак производной: (c⋅f)′=c⋅f′ Производная суммы: (f+y)′=f′+y′ Производная произведения: (f⋅y)′=f′⋅y+f⋅y′ Производная частного: (fy)′=f′y−fy′y2 Производная сложной функции: [f(y)]′=f′(y)⋅y′ Алгоритм нахождения производной от сложной функции Определяем «внутреннюю» функцию, находим ее производную. Определяем «внешнюю» функцию, находим ее производную. Умножаем результаты первого и второго пунктов.  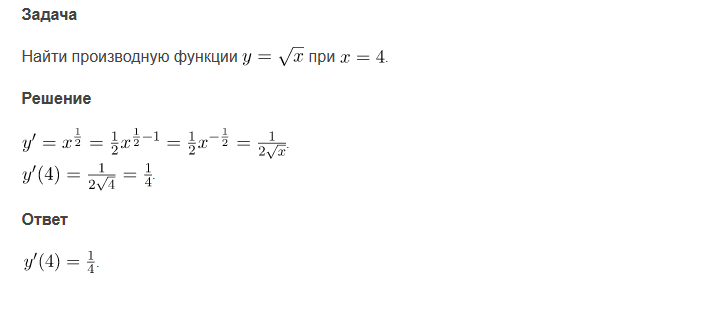 Дифференциалы высших порядков   5.Неопределенный и определенный интеграл, его свойства   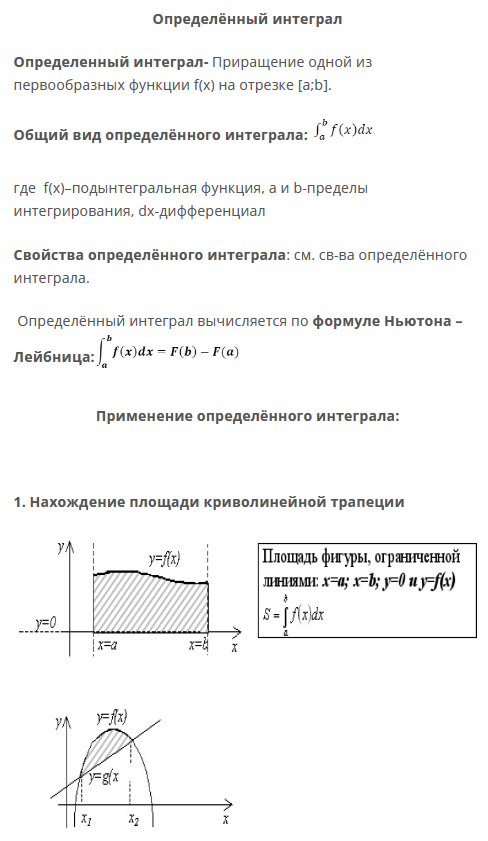 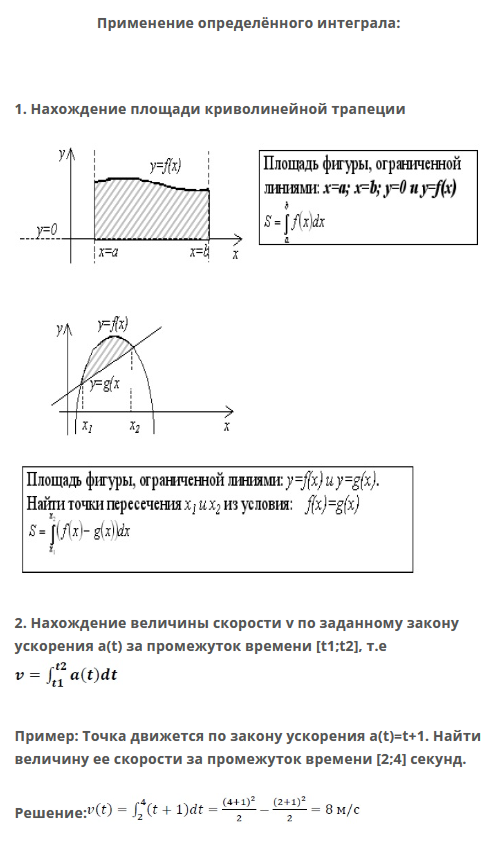  6.Предел и непрерывность функции нескольких переменных. Производная высших порядков. Частные производные.          |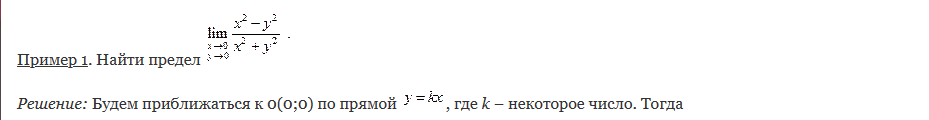
