Самостоятельная. Самостоятельная работа по теме 1. 1 Линейные уравнения и неравенства. Дробнорациональные уравнения. Уравнения, содержащие мод
 Скачать 225.39 Kb. Скачать 225.39 Kb.
|
|
Самостоятельная работа по теме 1.1. Линейные уравнения и неравенства. Дробно-рациональные уравнения. Уравнения, содержащие мод. Задание 1. Линейные уравнения с одной переменной. 1. Дайте определение уравнения с одной переменной. 1. Уравнения с одной переменной называются, если нужно найти те значения переменной, при которых получается верное числовое равенство. 2. Как записывается в общем виде линейное уравнение? 2. ax+b= 0 ax=-b x=- a/b 3. Какие уравнения называются равносильными? 3. Уравнения называются равносильными, если множества их решений равны. 4. Что называется корнем уравнения? 4. Корнем уравнения называются значение переменной, при подстановке которого в уравнение получается верное числовое равенство. 5. Сформулируйте теоремы, на основании которого решаются линейные уравнения. 5. 1- Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение, равносильному данному. 2- Если к обеим частям уравнения умножить или разделить на одно и то же число  0, то получается уравнение, равносильное данному. 0, то получается уравнение, равносильное данному.6. Какой вид имеют линейные уравнения, имеющие одно решение, не имеющие решения и имеющие бесконечное множество решений? 6. 1- уравнение 5х+4=0 имеет единственное решение х =— 5/4; 2-уравнение 3х=О имеет единственное решение х=О; 3-уравнение О*х+2=О не имеет решения, так как при любом значении х произведение О*х=О и О+2  О; О;4-уравнение О*х=О имеет бесконечное множество решений, любое число является решением этого уравнения. 7. Какие уравнения называются дробно-рациональными? 7. Дробным рациональным уравнением называется уравнение, обе части которого являются рациональными выражениями, причём хотя бы одно из них - дробным выражением. 8. Как выполняется графическое решение линейных уравнений? 8. Графический способ решения линейных уравнений. Уравнение вида ах=Ь, к которому может быть сведено любое линейное уравнение, можно решить графическим способом. На одном и том же чертеже построим графики двух функций: у=ах и у=Ь. Если эти графики пересекутся, то абсцисса их точки пересечения и будет корнем уравнения ах=Ь. Если графики не будут иметь точки пересечения, то уравнение не будет иметь корней. 9. Как графически изображается линейное уравнение, имеющее одно решение, не имеющее решения и имеющее бесконечное множество решений? 9. 1. А  О. Графиком функции у=ах будет прямая, проходящая через начало координат, наклоненная к оси Ох под некоторым углом a. Графиком функции у=Ь является прямая, параллельная оси Ох. Эти две прямые пересекаются в единственной точке М. Абсцисса точки пересечения b/a и есть корень уравнения ах=Ь. О. Графиком функции у=ах будет прямая, проходящая через начало координат, наклоненная к оси Ох под некоторым углом a. Графиком функции у=Ь является прямая, параллельная оси Ох. Эти две прямые пересекаются в единственной точке М. Абсцисса точки пересечения b/a и есть корень уравнения ах=Ь.2- а=О, Ь  О. В этом случае прямая у=ах совпадает с осью Ох, а прямая у=Ь параллельна оси Ох. Прямые у=ах и у=Ь оказались параллельными. Эти прямые не имеют точки пересечения, поэтому уравнение ах=Ь не имеет корней. О. В этом случае прямая у=ах совпадает с осью Ох, а прямая у=Ь параллельна оси Ох. Прямые у=ах и у=Ь оказались параллельными. Эти прямые не имеют точки пересечения, поэтому уравнение ах=Ь не имеет корней.3- а=Ь =О. В этом случае прямые у=ах и у=Ь совпадают, сливаясь с осью Ох. Можно утверждать, что эти прямые пересекаются в каждой точке оси Ох, поэтому любое число является корнем уравнения ах=Ь. 10. Дайте определение модуля действительного числа. 10. Модуль действительного числа равен самому числу х, если х положительное число, или равен числу -x, если х отрицательное число. Модуль нуля равен нулю. 11. Перечислите основные свойства модуля действительного числа. 1. Два противоположных числа имеют один и тот же модуль: lal=l-al, модуль числа не изменится, если число умножить на (-1). 2. Модуль не может быть отрицательным числом: lal≥0. 3. Число не может быть больше своего модуля: a≤lal. 4. Модуль суммы действительных чисел не больше суммы их модулей : la+bl≤lal+lbl. 5. Модуль разности двух чисел не меньше разности модулей этих чисел: la-bl≥lal-lbl. 6. Модуль произведения нескольких чисел равен произведению их модулей: lа*bl=lal*lbl. 7. Модуль целой степени какого-либо числа равен степени его модуля: lan l = laln . 8. Модуль частного двух чисел равен частному их модулей: 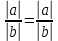 , b≠0. , b≠0.12. Что называется системой двух уравнений с одной переменной? 12.Системой двух предложений А(х) и В(х) называется предложение, которое записывается с помощью фигурной скобки (здесь А(х), В(х) — уравнения или неравенства с одной переменной): 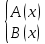 Число х0 называют решением системы, если оно является решением каждого из предложений А (х) и В(х). Число х0 называют решением системы, если оно является решением каждого из предложений А (х) и В(х).13. Что называется совокупностью двух уравнений с одной переменной? 13. Совокупностью (объединением) двух предложений А(х) и В(х) называется предложение «А(х) или В(х)», которое записывается с помощью квадратной скобки. Число х0 называется решением совокупности, если х0 является решением хотя бы одного из предложений А(х) или В (х). 14. В чем состоит различие между системой и совокупностью двух уравнений с одной переменной? 14. 1) Система - значок: { Обозначает пересечение решений. Т. е. некое множество (конкретные решения, или целый промежуток), где выполняются ВСЕ из равенств и/или неравенств системы. 2) Совокупность - значок: [ Обозначает объединение решений. Т. е. некое множество (конкретные решения, или целый промежуток), где выполняется одно из равенств и/или неравенств системы. 15. Как выполняется решение линейных уравнений, содержащих переменную под знаком модуля? 15. При решении уравнений, содержащих переменную под знаком модуля, будем руководствоваться определением модуля: x, если x>0 |x|= 0, если x=0 -x, если x<0 Решим уравнение |х-5|=4. Исходя из определения модуля, произведем следующие рассуждения. Если выражение, стоящее под знаком модуля неотрицательно, то есть х-5≥0, то уравнение примет вид х-5=4. Если значение выражения под знаком модуля отрицательно, то по определению оно будет равно – (х-5)=4 или х-5= -4. Решая полученные уравнения, находим: х1=9, х2=1. Ответ: 9; 1 16. Как графически выполняется решение линейных уравнений. содержащих переменную под знаком модуля? Решить уравнение lxl = 3. РЕШЕНИЕ. По определению модуля: (lxl = з)  Решим это уравнение графическим способом. Построим графики функций у =|x| и у = З. Для построения графика функции у=|x| строим прямые у = х и у =-х. График функции у =|x| есть сплошная линия, симметричная относительно оси ординат и расположенная выше оси абсцисс (lxl — число положительное, следовательно, график расположен выше оси абсцисс). При х > 0 график совпадает с прямой у = х, а при х < 0 — с прямой у = х. Далее строим прямую у = З. График функции у = х пересекается с прямой у = З в двух точках М1 и М2 с абсциссами х = З и x=-3, которые являются корнями уравнения |х| = З. 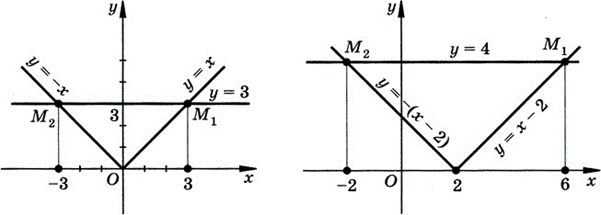 Линейные неравенства. 1.Что называется неравенством? 2. Какие выражения называются алгебраическими и какие числовыми неравенствами? 3. Что называется решением неравенства? 4. Какие неравенства называются равносильными? 5. Перечислите основные свойства неравенств. 6. Какие неравенства называются линейными? 7. Какие неравенства не имеют решения? 8. Какому неравенству удовлетворяет любое число? 9. В каких случаях решение неравенства сводится к решению совокупности неравенств? 10. Как записываются решения неравенств вида lxl < а и lxl > а? 1. Два алгебраических выражения или два числа, соединенные знаком больше или меньше, называются неравенствами. 2. Неравенства могут быть как числовыми: 5 > З; -8 < -3; -7 < 5, так и алгебраическими: а > Ь; а2 > 0; а + Ь < с + d. 3. Решением неравенства называется значение переменной, при котором неравенство истинно (обращается в верное числовое неравенство). Решить неравенство — значит найти множество его решений. 4. Неравенства называются равносильными, если множества их решений равны. 5.  6. Линейные неравенства. Линейным неравенством называется неравенство вида ах + Ь > 0 (или ах + Ь < 0). 7. Решение системы может не содержать ни одной точки; в этом случае говорят, что система решений не имеет. Система неравенств не имеет решений, если хотя бы одно из неравенств системы не имеет решений. 8. 0⋅x9. Несколько неравенств с одной переменной образуют совокупность неравенств, если нужно найти все такие значения переменной, каждое из которых является решением хотя бы одного из заданных неравенств. Каждое такое значение переменной называют частным решением совокупности неравенств. Множество всех частных решений совокупности неравенств представляет собой решение совокупности неравенств. Решение совокупности неравенств — объединение решений неравенств, входящих в совокупность. 10. ( |x| < a ) Задание 2. №1) 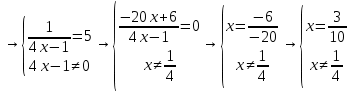 Ответ:  №2)  Ответ:  №3)  Ответ:x=-13 №4)  Ответ: x=-0,5 №5)  Ответ:x= 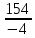 или или 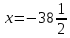 №6) 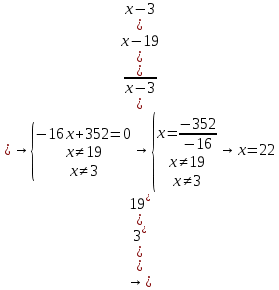 Ответ:x=2 №7) 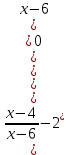 Ответ:x=8 №8) 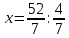 x=13 x=13Ответ:x=13 №9)  Ответ:x=-5 №10)  Ответ:x= 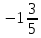 №11) 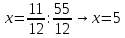 Ответ:x=5 №12) 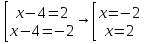 Ответ: x1,2=  Задание 3. №1) 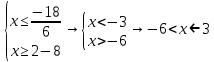 Ответ: -6 < x < -3 №2) 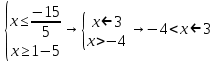 Ответ: -4 < x < -3 №3)  Ответ: 2 ≤ x < 3 Задание 4. 1. ∣7x−4∣=8 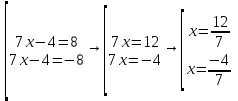 Ответ: 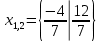 2. ∣6+5x∣=2 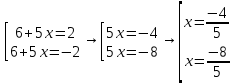 Ответ: x1,2=  3. ∣8−x∣=1  Ответ: x1,2=  Задание 5. 1. 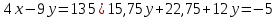 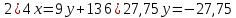 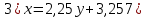 y=-1 y=-1 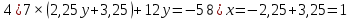 Ответ:x=1, y=-1 2. 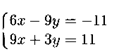 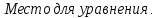 Ответ:x2/3, y5,3 |
