1. Магнит рісі. Магнит рісіні асиеттері. Магнит индукция векторы. Макротоктар жне микротоктар. B мен h арасындаы байланысты жазыыз
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
Бор теориясын сутегі атомына қолдануСутегі атомында электрон ядроның айналасында Кулондық тартылу күшінің әсерінен радиусы -ге шеңберлік орбитамен қозғалады. Сондықтан электронды осы орбитада ұстап тұратын центрге тартқыш күш электрон мен ядро арасындағы Кулондық күшке тең болады: 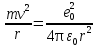 . Импульс моментінің квантталу ережесін ескерсек, алатынымыз: 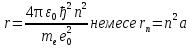 мұндағы: n=1,2,3,… Сутегі атомындағы электронның орбитасы тек дискретті мәндерді қабылдайды, яғни квантталады. n=1 тең болғанда сутегі атомындағы электронның бірінші орбитасының мәні алынады: 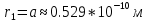 . Бұл мән бірінші Бор радиусы деп аталады. . Бұл мән бірінші Бор радиусы деп аталады.Сутегі атомының стационар күйінің энергиясы: 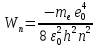 мұндағы: n -бас кванттық сан. Бас кванттық сан атом энергиясының деңгейін анықтайды. n=1 атомның негізгі күйі, n>1 атомның қозған күйі деп аталады. Сутегі атомының энергиясы тек дискретті мәндерді қабылдайды, яғни квантталады. 13.Заттардың корпускулалық-толқындық қасиеттері. Де-Бройль толқындарының кейбір қасиеттері. Физикалық объект бір мезгілде корпускулалық және толқындық қасиеттерге ие болса, онда мұны корпускулалық-толқындық дуализмі деп атайды. Корпускулалық-толқындық дуализмді классикалық ұғымдармен түсіндіре алмаймыз, себебі фотонды әрбір уақыт мезетінде кеңістікте белгілі бір орын алатын нүктелік объект деп қарастыруға болмайды. Жеке фотонды электр өрісінің кернеулігімен сипаттауға болмайды. Фотон дегеніміз – электромагниттік сәуле шығарумен байланыста болатын физикалық объект, ол энергиямен және импульспен сипатталады. Классикалық физикада бөлшек пен толқынның табиғатын әртүрлі деп қарастырады. Бөлшек дискретті, кеңістікте өте аз көлем алады, ал толқын болса кеңістікте өте үлкен орын алады. Толқын бір ортадан екінші ортаға өткенде жартылай сынып, екінші ортада таралады, ал жартысы шағылып, интерференциаланады. Бөлшек болса біртұтас, ол интерференциаланбайды. Бірақ ХІХ ғ. 20-жылдарында физикада табиғаттың фундаментальды заңы ашылды, ол заттың корпускулалық-толқындық дуализмі деп аталады, мұнда бөлшек пен толқын туралы түсініктер біріктірілді. Де Бройль идеясы бойынша, дуализм тек оптикалық құбылыстарға ғана тән емес, оның универсалды мәні бар, яғни корпускулалық-толқындық қасиеттер тек қана фотонмен бірге, 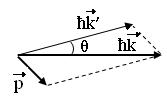 барлық бөлшектерде болады; мысалы, электронда да болады. Сонымен Де Бройль теориясы бойынша кез келген микрообъектінің бір жағынан корпускулалық сипаттамалары болады: энергия W , импульс P , екінші жағынан толқындық сипаттамалары болады: жиілік барлық бөлшектерде болады; мысалы, электронда да болады. Сонымен Де Бройль теориясы бойынша кез келген микрообъектінің бір жағынан корпускулалық сипаттамалары болады: энергия W , импульс P , екінші жағынан толқындық сипаттамалары болады: жиілік 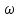 , толқын ұзындығы λ . Кез келген бөлшектің корпускулалық-толқындық сипаттамалары дәл фотонның сипаттамалары сияқты байланысқан: , толқын ұзындығы λ . Кез келген бөлшектің корпускулалық-толқындық сипаттамалары дәл фотонның сипаттамалары сияқты байланысқан: 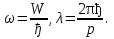 Еркін қозғалатын бөлшек ретінде қарастырылатын толқын де Бройль толқыны деп аталады. 14.Анықталмағандыққатынастардыжазыптүсіндіріңіз? Анықталмағандық принципі— физикалық жүйені сипаттайтын шамалардың бір мезгілде дәл мәндер қабылдай алмайтындығын тұжырымдайтын кванттық теорияның іргелі қағидасы. 1927 ж. неміс физигі Вагнер Гейзенбергашқан. Анықталмағандық принципі материя бөлшектерінің корпускулалық-толқындық табиғаты болатындығын айқындайды. Сандық тұрғыдан Анықталмағандық принципі былай тұжырымдалады: егер — жүйенің инерция центріндегі координатының анықталмағандық мәні, ал импульсының осіне проекциясының анықталмағандық мәні болса, онда осы анықталмағандықтардың көбейтіндісі Планк тұрақтысынан 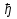 кем болмайды Макроскопиялық шамалармен салыстырғанда аз шама болғандықтан, бұл қатынас атомдық масштабтағы құбылыстарға қатысты ғана орындалады. Анықталмағандық принципі атом ішіндегі құбылыстардың заңдылықтарын түсіндіру және кванттық механика саласының қалыптасуы кезінде аса маңызды рөль атқарды. кем болмайды Макроскопиялық шамалармен салыстырғанда аз шама болғандықтан, бұл қатынас атомдық масштабтағы құбылыстарға қатысты ғана орындалады. Анықталмағандық принципі атом ішіндегі құбылыстардың заңдылықтарын түсіндіру және кванттық механика саласының қалыптасуы кезінде аса маңызды рөль атқарды. Егер {\displaystyle \Delta x} 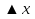 және {\displaystyle \Delta p} және {\displaystyle \Delta p}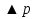 сәйкесінше координаттың және импульстың орташа квадраттық ауытқулары болса: сәйкесінше координаттың және импульстың орташа квадраттық ауытқулары болса: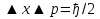 {\displaystyle \Delta x\Delta p\geqslant {\frac {\hbar }{2}}}мұндағы {\displaystyle \hbar } 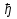 — келтірілген Планк тұрақтысы. Анықталмағандық қатынасы - екі орайлас физикалык шамалар мәніндегі анықталмағандықтардың көбейтіндісі (мысалы, импульс пен координатаның, энергия мен уақыттың) Планк тұрақтысынан кіші болуы мүмкін емес дейтін тұжырым. — келтірілген Планк тұрақтысы. Анықталмағандық қатынасы - екі орайлас физикалык шамалар мәніндегі анықталмағандықтардың көбейтіндісі (мысалы, импульс пен координатаның, энергия мен уақыттың) Планк тұрақтысынан кіші болуы мүмкін емес дейтін тұжырым. 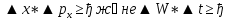 қатынастары анықталмағандық қатынастары деп аталады. Анықталмағандақ қатынастарын бірінші рет 1927 ж. В.Гейзенберг орнатты. Екі түйіндес айнымалының анықталмағандық мәндерінің көбейтіндісі Планк ħ тұрақтысынан аз болмайды деген тұжырым Гейзенбергтің анықталмағандық принципі деп аталады.Гейзенбергтің анықталмағандық принципі кванттық механикадағы фундаменталды қағидаларының бірі болып табылады және корпускулалық-толқындық дуализммен байланысты. қатынастары анықталмағандық қатынастары деп аталады. Анықталмағандақ қатынастарын бірінші рет 1927 ж. В.Гейзенберг орнатты. Екі түйіндес айнымалының анықталмағандық мәндерінің көбейтіндісі Планк ħ тұрақтысынан аз болмайды деген тұжырым Гейзенбергтің анықталмағандық принципі деп аталады.Гейзенбергтің анықталмағандық принципі кванттық механикадағы фундаменталды қағидаларының бірі болып табылады және корпускулалық-толқындық дуализммен байланысты.15.Толқындық функция және оның қасиеттерін жазыңыз? Микробөлшектерді бейнелеу үшін ықтималдық амалды қолдану қажеттігі квантық теорияның маңызды өзгешелігі болып табылады. Сонда де-Бройль толқындарын ықтималдық толқындары ретінде мағыналауға, яғни микробөлшектердің кеңістіктің әртүрлі нүктелерінде табылу ықтималдығы толқындық заң бойынша өзгереді деп санауға бола ма? – деген сұрақ туады. Де-Бройль толқындарын осылай түсіндіруге болмайды, өйткені осы жағдайда кеңістіктің кейбір нүктелерінде бөлектің табылу ықтималдығы теріс болуы мүмкін, бұл мағынасыздық. Осы қиындықты жою үшін 1926 ж. неміс физигі М. Борн толқындық заң бойынша ықтималдықтың өзі емес, ықтималдық амплитудасы деп аталатын шама өзгереді деп ұйғарды. Осы шама Сонымен, кеңістіктің қайсыбір нүктесінде берілген уақыт мезетінде бөлшектің табылу ықтималдығының үлестірілуін бейнелеу үшін толқындық функция (немесе пси-функция) деп аталатын Бөлшектің Физикалық мағынаға функциясының өзі емес, оның модулінің квадраты яғни кеңістіктің берілген нүктесінде бөлшектің табылу ықтималдығын анықтайды. Басқа сөзбен айтқанда, Бөлшектің орнын барлық кеңістік бойынша қарастыру керек. Бөлшектің әйтеуір бір жерде болатындығы ақиқат, демек, бөлшекті бүкіл көлемнің әйтеуір бір жерінде табылу ықтималдығы ақиқат нәрсе. Осындай жағдайдың ықтималдығы бірге тең. Сондықтан 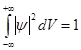 немесе немесе 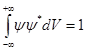 . (5) . (5)Осы теңдік нормалау шарты деп аталады, ал осы шартты қанағаттандыратын функциясы нормаланған болады. Толқындық функция микробөлшектер күйінің негізгі сипаттамасы болып табылады. Бұл — толқындық теңдеу және одан тәжірибелерде бақыланатын бөлшектердің толкындық қасиеттері шығады. Кванттық механикада бөлшектің күйін толқындық функциямен сипаттайды. Толқындық функция — координаталар мен уақыттың комплекстік функциясы, оның айқын түрі Шредингер теңдеуінің шешуінен шығады да, соңында бөлшекке әрекет ететін күштердің сипатымен анықталады. 16.Жалпы Шредингер теңдеуін және стационарлық күйлер үшін Шредингер теңдеуін жазыңыз. Еркін бөлшектің қозғалысын түсіндіріңіз? Классикалық механикада күш және өріс әсерінен қозғалатын бөлшектің координаттары мен импульстарының бұрынғы және болашақ мәндерін қозғалыс теңдеуі арқылы бірмәнді анықтауға болады (егер бұлардың қайсыбір уақыт мезетінде мәндері берілген болса). Ал микробөлшектер үшін бұл әдіс қолдануға келмейді. Себеп мынада. Микробөлшектердің корпускулалық әрі толқындық қасиеттері болатындығына әбден көз жеткізілді. Осыдан әр түрлі күш өрістерінде бөлшектің қозғалысын қарастырғанда бұлардың толқындық табиғатын ескеру қажет екендігі келіп шығады. Сонды бөлшек қозғалысын бейнелеу үшін толқындық функция пайдаланылады. Ендігі негізгі мәселе толқындық функцияның кеңістіктегі және уақыт бойынша өзгерісін бейнелейтін жалпы заңды немесе толқындық өрістің қозғалыс заңын тағайындау болып табылады. Зат бөлшектерінің толқындық қасиеттері жайындағы де-Бройль идеясын дамыта келе, австрия физигі Э. Шредингер өзінің атақты теңдеуін ұсынды (1926). Осы теңдеу әр түрлі күш өрістерінде қозғалатын бөлшектің толқындық функцияларын табуға мүмкіндік береді. Шредингер теңдеуі былай жазылады: мұндағы т – бөлшек массасы, і – жорамал бірлік, U – бөлшектің потенциалдық энергиясы, Шредингер теңдеуі – бұл Ньютон механикасының теңдеулері, электромагниттік өріс үшін Максвелл теңдеулерімен және т.б. қатар қазіргі заманғы физиканың іргелі теңдеулерінің бірі, және де ол қорытылып шығарылмайды. Оны бастапқы негізгі ұйғарым деп қарастыру керек. Шредингер теңдеуінің дұрыстығы теория нәтижелерінің эксперимент деректерімен толық үйлесуімен, және де практикада қолданыс тапқан, мысалы, мазерлерде, лазерлерде, жартылай өткізгішті қондырғыларды және т.т. көптеген болжаулармен расталады. Кванттық теорияда ерекше ролді стационарлық күйлер атқарады, бұларда барлық бақыланатын физикалық шамалар уақыт өткенде өзгермейді. Стационарлық күйлер үшін Шредингер теңдеуі: Оны мына түрде жазуға болады: Шредингер теңдеуі берілген күйдің толқындық функциясын табуға, демек кеңістіктің әр түрлі нүктелерінде бөлшектің болу ықтималдығын анықтауға мүмкіндік береді. Бөлшектің еркін қозғалысы кезінде оның толық энергиясы кинетикалық энергиясына тең болады. Бұл жағдай үшін Шредингер теңдеуі келесі түрде жазылады: 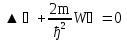 . .Бұл теңдеудің шешімі Еркін электронның қозғалысына монохроматты жазық де Бройль толқыны сәйкес келеді. 17.Бөлшектің шексіз биік қабырғалары бар бірөлшемді тікбұрышты потенциалдық шұңқырдан өтуі. Бөлшектің потенциялдық тосқаулдан өтуін және тунельдік эффектіні түсіндіріңіз? Айталық элементар бөлшек бір өлшемді шексіз терең шұңқырдың ішінде қозғалыста болсын. Бөлшектің қозғалысы x осінің бойымен бағытталсын. Сонда бөлшектің қозғалысы қабырғалары x=0 және x=d шектелген тік бұрышты потенциалдық шұңқырдың ішінде болуына сәйкес, оның потенциалдық энергиясы шұңқырдың ішінде нөлге тең U=0; ал координаттары x<0 және x>d болатын сыртқы жақтарындағы потенциалдық энергияның мәндері шексіздікке өседі, U→  . Сөйтіп, бөлшек қабырғалары шексіз потенциалдық шұңқырдың сыртындағы энергияның мәні ішіндегі энергиядан әлдеқайда көбірек болады Ushn>>U0. Бөлшек осінің бағытымен қозғалыста болғандықтан, ѱ функциясы осы бір координатқа тәуелді болуына сәйкес Шредингердің теңдеуін осы бөлшек қозғалысы үшін мына түрде жазуға болады . Сөйтіп, бөлшек қабырғалары шексіз потенциалдық шұңқырдың сыртындағы энергияның мәні ішіндегі энергиядан әлдеқайда көбірек болады Ushn>>U0. Бөлшек осінің бағытымен қозғалыста болғандықтан, ѱ функциясы осы бір координатқа тәуелді болуына сәйкес Шредингердің теңдеуін осы бөлшек қозғалысы үшін мына түрде жазуға болады▲ѱ+  (1) (1)мұндағы . ▲ѱ+  Егер бөлшек потенциалдық шұңқыр ішінде десек, яғни  болса, онда теңдеу мынадай түрде жазылады (U=0) болса, онда теңдеу мынадай түрде жазылады (U=0)▲ѱ+ 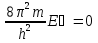 (1) теңдеудің жалпы шешуі болып мына өрнек есептеледі (1) теңдеудің жалпы шешуі болып мына өрнек есептеледі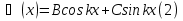 мұндағы B және C - тұрақты шамалар да, 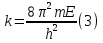 Бұдан бөлшектің кинетикалық энергиясы 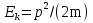 оның потенциалдық шұңқырдан шығып кетуіне жеткіліксіз болса, онда x=0 және x=d болғанда ғана толқындық функцияның мәні нөлге айналады. Олай болса, x=0 болғанда ѱ=0 болып, (2) теңдеудің оң жағындағы екі мүшесі де нөлге айналады. Сонда B+C=0 болар еді де, B= - C. Бұдан функцияның мәні мынадай түрге келеді оның потенциалдық шұңқырдан шығып кетуіне жеткіліксіз болса, онда x=0 және x=d болғанда ғана толқындық функцияның мәні нөлге айналады. Олай болса, x=0 болғанда ѱ=0 болып, (2) теңдеудің оң жағындағы екі мүшесі де нөлге айналады. Сонда B+C=0 болар еді де, B= - C. Бұдан функцияның мәні мынадай түрге келедіѱ (x)=2B sin kx (4) Ал x=d болса, онда ѱ=0 да, 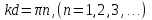 , ,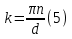 Енді осы k-ның мәнін (3) формулаға қойып мына өрнекті аламыз: 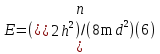 Сонымен потенциалдық шұңқыр ішіндегі бөлшектің толық энергиясының кез келген мәні болмай, тек 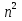 санына сәйкес белгілі бір мәндері ғана бола алады. Сөйтіп бөлшектің энергиясы квантталған болып шығады. (6) формуладағы n-нің орнына белгілі бір сан мәндерін қою арқылы потенциалдық шұңқыр ішіндегі бөлшектің энергетикалық деңгейлерін (E1, E2, E3,…) анықтауға болады. Мұндағы - бөлшектің энергетикалық деңгейлерін сипаттайтын кванттық сандар деп аталады да, бөлшектің қандай кванттық күйде екендігін көрсетеді. Олай болса, кванттық санының мәніне сәйкес оның кинетикалық энергиясының (Ek) мәндері өзгеріп отырады. Енді сыбайлас екі энергетикалық деңгейдің аралығындағы энергияның өзгерісі мынадай болсын санына сәйкес белгілі бір мәндері ғана бола алады. Сөйтіп бөлшектің энергиясы квантталған болып шығады. (6) формуладағы n-нің орнына белгілі бір сан мәндерін қою арқылы потенциалдық шұңқыр ішіндегі бөлшектің энергетикалық деңгейлерін (E1, E2, E3,…) анықтауға болады. Мұндағы - бөлшектің энергетикалық деңгейлерін сипаттайтын кванттық сандар деп аталады да, бөлшектің қандай кванттық күйде екендігін көрсетеді. Олай болса, кванттық санының мәніне сәйкес оның кинетикалық энергиясының (Ek) мәндері өзгеріп отырады. Енді сыбайлас екі энергетикалық деңгейдің аралығындағы энергияның өзгерісі мынадай болсын▲E=En+1-En=(2+1) 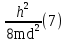 Бұл формуладағы n кванттық санының мәні артқан сайын энергетикалық деңгейлердің ара қашықтығының өсетіндігін (мысалы E3 және E4 )байқаймыз. Сонымен қатар бұл аралықтағы энергияның шамасы ( 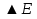 ) потенциалдық шұңқырдың енділігі d-z - ке кері пропорционал екендігін көріп отырмыз. Мысалы, металл өткізгіштің ішіндегі еркін электронның өлшемі ) потенциалдық шұңқырдың енділігі d-z - ке кері пропорционал екендігін көріп отырмыз. Мысалы, металл өткізгіштің ішіндегі еркін электронның өлшемі 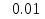 м болса, онда оның көрші екі деңгей аралығындағы энергиясының шамасы мынаған тең: м болса, онда оның көрші екі деңгей аралығындағы энергиясының шамасы мынаған тең: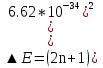 Яғни электронның энергетикалық деңгейлері бір-біріне өте тығыз орналасқандықтан, олардың спектрлері үздіксіз болып келеді. Бұдан металдағы электрон энергиясының үздіксіз өзгеретіндігін байқаймыз. Егер де потенциалдық шұңқырдың ұзындық өлшемдері атомның өлшеміне шамалас болса, яғни d  м, онда энергия аралығының шамасы мынадай болады: м, онда энергия аралығының шамасы мынадай болады: Сөйтіп, энергияның дискретті мәні анық білінеді де, спектрлер сызықты болып келеді. Қорыта келе, бұл мысалдардан қабырғалары өте шексіз биік потенциалдық шұңқырдың ішіндегі бөлшекке Шредингер теңдеуін қолданғанда, оның энергиясының кванттық мәндерінің бар болатынын көрсетеді. Ал классикалық физикада бөлшектің энергиясына ешқандай шек қойылмағандығын білеміз. Сонымен бөлшектің күйін сипаттайтын кванттық санының мәні артқан сайын энергетикалық деңгейлердің аралықтары бір-біріне өте жақындап тығыздала береді де, олардың дискретті мәні білінбей тұтасып бірыңғай орналаса бастайды.Осы қағида Бордың сәйкестік принципі деп аталады. Осындай пікірге сәйкес кванттық санның мәндері артқан сайын кванттық механиканың заңдары классикалық физика заңдарына ауысады. Бұл қорытындыны былайша түсінуге болады. Жалпы түрдегі, классикалық физиканы жоққа шығармай, тек оның қолданылу шектерін ғана көрсетеді де, ал кейбір жағдайларда жаңа теорияның өзі ескі теорияға ауыса алады. 18. Кванттық механикадағы осилятор ұғымын түсіндірің? |
