вар 4. 1. Марковский процесс с дискретными состояниями и дискретным временем
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
13. Разложение времени сетевой задержки по каналам сети jk – Трафик (traffic), поступающий в сеть из внешних источников для тех сообщений, которые возникают в узле j и предназначены для узла k. Полный внешний трафик, поступающий в сеть, определим как: 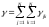 , где N – число узлов. , где N – число узлов.Обозначим T – средняя задержка сообщения, Zjk – задержка сообщения, которое возникло в j и предназначено для узла k. Ясно, что эти две средние величины связаны равенством: 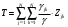 , ,так как доля (jk/) полного входящего трафика сообщений имеет в среднем задержку равную Zjk. Отметим, что последнее равенство представляет разложение сети по парам источник-адресат. Обозначим через jk путь, по которому идут сообщения, возникающие в узлеj и имеющие в качестве узла назначения узел k. Говорят, что i-ый канал (с пропускной способностью Ci) включен в путь jk, если сообщения, идущие по этому пути, проходят указанный канал (Cijk). Тогда среднее число сообщений в единицу времени, проходящих по i-му каналу связи равно: 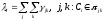 Кроме того, заметим что Zjk – сумма (Ti) средних задержек, испытываемых сообщением при передаче по различным каналам пути jk. 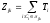 Следовательно: 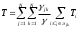 Изменим теперь порядок суммирования (условие на i сменим на пару jk). 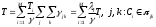  Теперь средняя задержка представляет разложение по отдельным каналам. Используя известный результат исследований Джексона: Канал сети можно рассматривать как такой же канал, действующий независимо от сети, но с пуассоновским входным потоком, интенсивность которого равно интенсивности, задаваемой сетью. 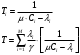 и 1/ - средняя длина сообщения, 1/  Сi – среднее время передачи сообщения по каналу Сi. Сi – среднее время передачи сообщения по каналу Сi. Можно провести расчет для случая непоказательных длин сообщений. Но при этом будет проявлена слишком большая смелость, так как для систем M/G/1 результат Джексона неприменим. Однако это приближение приводит к модели, которая очень хорошо согласуется с моделированием на ЭВМ. 14. Задача выбора пропускных способностей каналов Предположим, что заданы потоки 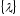 и топология сети. и топология сети.Необходимо минимизировать время пребывания требования в сети, удовлетворяющее ограничению: 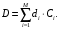 Для решения задачи будем варьировать пропускными способностями каналов 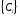 , , 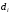 - стоимость пропускной способности для i-ого канала. - стоимость пропускной способности для i-ого канала.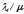 -среднее число бит в секунду, которые проходят по i-ому каналу, и, следовательно, любое реализуемое решение задачи должно быть таким, чтобы i-тый канал имел пропускную способность, не меньше указанной величины, т.е. -среднее число бит в секунду, которые проходят по i-ому каналу, и, следовательно, любое реализуемое решение задачи должно быть таким, чтобы i-тый канал имел пропускную способность, не меньше указанной величины, т.е.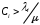 . . Для минимизации Т - времени пребывания требования в сети составим функцию Лагранжа: 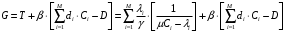 Как обычно, используя метод Лагранжа, получаем следующую систему из М уравнений 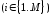 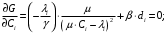 Решая относительно 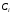 , получим: , получим: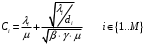 Определим , составив ограничение путем перемножения на 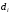 и суммировав по i: и суммировав по i: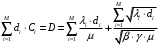 Следовательно: 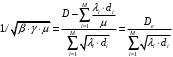 где 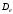 - добавочная стоимость. - добавочная стоимость.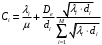  При таком наборе пропускных способностей каждый канал будет иметь, по крайней мере, пропускную способность 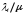 и, кроме того, некоторую дополнительную пропускную способность. и, кроме того, некоторую дополнительную пропускную способность.Минимальная средняя задержка сети, пропускные способности в которой выбраны оптимально, может быть записана в виде: 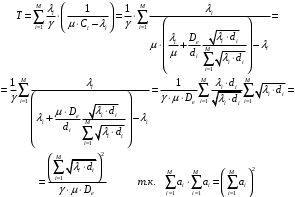 В 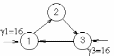 ернемся к рассмотренному ранее примеру. 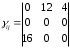 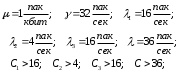 если 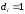 , что имеет место при рассмотрении каналов связи геостационарных с , что имеет место при рассмотрении каналов связи геостационарных с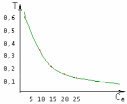 путников. В этом случае: путников. В этом случае: 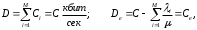 тогда: тогда: 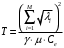 . Если потребовать, что . Если потребовать, что 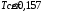 , то необходимо выбрать: , то необходимо выбрать: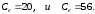 Тогда: 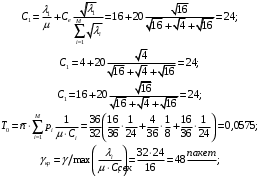  Для рассмотренного ранее примера  имели значения: имели значения: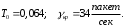 15. СМО типа M/M/1 Введем следующие обозначения:  – средняя норма прибытия, интенсивность входного потока – средняя норма прибытия, интенсивность входного потока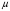 – средняя норма обслуживания, интенсивность потока обслуживания – средняя норма обслуживания, интенсивность потока обслуживания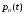 – вероятность того, что в системе в момент времени – вероятность того, что в системе в момент времени 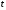 находится ровно находится ровно  требований требованийВычислим 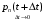 – вероятность того, что в системе момент времени – вероятность того, что в системе момент времени 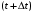 находится ровно находится ровно  требований. требований.Для этого определим вероятность того, что за время 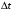 произошло одно прибытие (одно обслуживание). произошло одно прибытие (одно обслуживание).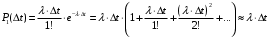 Так как простейший поток обладает свойством ординарности (за интервал времени 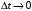 не может произойти более одного прибытия), то справедливо: не может произойти более одного прибытия), то справедливо: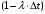 – вероятность того, что за время – вероятность того, что за время 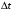 не произошло прибытий не произошло прибытий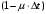 – вероятность того, что за время – вероятность того, что за время 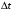 не было окончаний обслуживания не было окончаний обслуживанияРассмотрим случаи реализации события с вероятностью 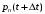 : :а) В момент времени 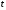 в системе находилось в системе находилось  требований, а за время требований, а за время 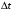 нет новых прибытий и окончаний обслуживания: нет новых прибытий и окончаний обслуживания: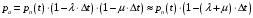 б) В момент времени 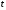 в системе находилось в системе находилось 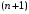 требований, а за время требований, а за время 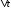 нет новых прибытий, и произошло обслуживание: нет новых прибытий, и произошло обслуживание: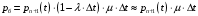 в) В момент времени 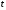 в системе находилось в системе находилось 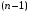 требований, а за время требований, а за время 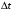 произошло одно прибытие, и нет окончаний обслуживания: произошло одно прибытие, и нет окончаний обслуживания: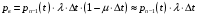 Вероятность 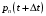 равна сумме вероятностей рассмотренных случаев: равна сумме вероятностей рассмотренных случаев: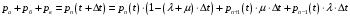 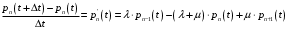 (1) (1)Эта формула справедлива для 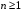 , а для , а для 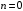 имеем: имеем:а) В момент времени 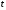 нет требований, а за время нет требований, а за время 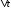 нет новых прибытий: нет новых прибытий: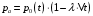 б) В момент времени 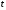 в системе 1 требование, а за время в системе 1 требование, а за время 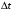 нет новых прибытий и окончаний обслуживания: нет новых прибытий и окончаний обслуживания: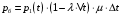 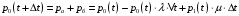 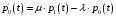 (2) (2)Уравнения (1) и (2) называют дифференциальными уравнениями Колмогорова для СМО типа 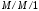 . .Для установившегося режима вероятность пребывания в системе  требований не зависит от времени, и поэтому справедлива система алгебраических уравнений: требований не зависит от времени, и поэтому справедлива система алгебраических уравнений: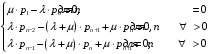 Методом математической индукции докажем, что 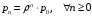 , где , где 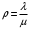 – параметр обслуживания. – параметр обслуживания.Доказательство: Для 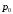 и и 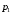 это справедливо, так как это справедливо, так как 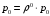 и и 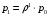 . Предположим, что справедливо . Предположим, что справедливо 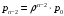 и и 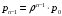 , тогда , тогда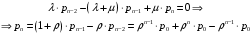 Вычислим 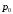 – вероятность того, что в системе нет требований. Пусть – вероятность того, что в системе нет требований. Пусть 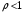 , тогда , тогда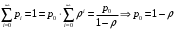 Тогда 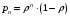 . .Представим СМО типа M/M/1 в виде графа, у которого вершины обозначают состояния системы, характеризующиеся числом требований, а ребра будут обозначать интенсивность перехода из одного состояния в другое. 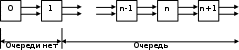 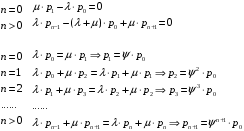 Вычислим среднее число требований N, находящихся в системе: 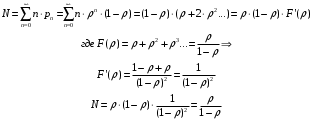 Так как всегда имеет место 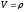 - среднее число требований в обсл. пр. - среднее число требований в обсл. пр.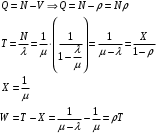 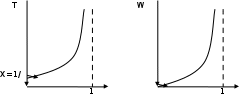 16. Одноканальная СМО с отказами (M/M/1/0) На вход поступает пуассоновский поток с интенсивностью . Заявка, заставшая канал занятым получает отказ и покидает систему. Обслуживание подчинено показательному закону с параметром . Единственный канал может находиться в одном из двух состояний: S0 – канал свободен, S1 – канал занят. 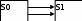 Пользуясь общим решением для схемы «гибели и размножения» получим: 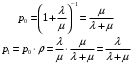 Очевидно, требование получит отказ, когда канал занят (доля необслуженных заявок). 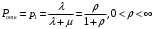 Доля обслуженных заявок – относительная пропускная способность: 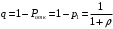 Абсолютная пропускная способность: 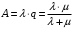 Время обслуживания равно  , если требование будет обслужено и равно 0, если нет. , если требование будет обслужено и равно 0, если нет.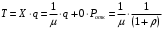 Пример. Система обработки информации представима в виде M/M/1/0. Интенсивность потока требований =9тр/час. Средняя продолжительность обработки tобр=5 мин. Определить T, W, X, N, Q, V, q, A, Pотк. Сравнить фактическую пропускную способность СМО с номинальной, которая была бы, если обработка информации длилась без перерыва.  Решение: Номинальная пропускная способность системы: 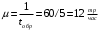 Относительная пропускная способность: 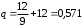 Таким образом, 57% заявок будет обслужено в установившемся режиме. Вероятность отказа Pотк=1-q=0,429. Значит около 49% требований получит отказ. Абсолютная (фактическая) пропускная способность обслуживающего прибора (канала): 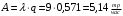 , ,что почти вдвое меньше, чем номинальная пропускная способность, это объясняется случайным характером потока заявок и потока обслуживания. 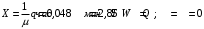 17. Одноканальная СМО с ограниченным ожиданием (M/M/1/k). В этой модели количество мест в очереди равно k, что и накладывает ограничение на время ожидания каждого требования, т. е. (W<k/). Время ожидания не превышает k обсл. Будем нумеровать состояния СМО по числу требований, находящихся в системе. S0 – канал свободен S1 – канал занят, очереди нет … Sk+1 – канал занят, в очереди k заявок  Пользуясь общим решением схемы «гибели и размножения» и введя обозначение =/, получим: 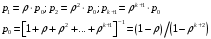 Выражение для p0 справедливо для <1, при: 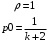 Заявка получает отказ, когда все k мест в очереди заняты: 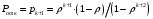 Оставшаяся доля заявок будет обслужена, поэтому относительная пропускная способность: 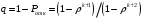 Абсолютная пропускная способность: A=  q. q.Выводы выражения для среднего времени ожидания пребывания в очереди (W). Любая заявка с вероятностью p0 не будет ждать обслуживания (время ожидания=0), с вероятностью p1 будет ждать одного обслуживания (время ожидания= 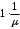 ), с вероятностью p2 будет ждать одного обслуживания (время ожидания= ), с вероятностью p2 будет ждать одного обслуживания (время ожидания=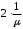 ) и т. д. ) и т. д.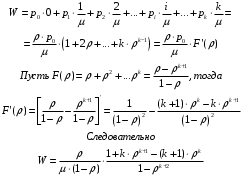 Время обслуживания X равно 1/, если заявка обслуживается и X=0, если она получила отказ. 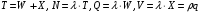 |
