вар 4. 1. Марковский процесс с дискретными состояниями и дискретным временем
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
7. Замкнутая многоканальная СМО (M/M/m/k/l) Эта достаточно общая система является наиболее сложной из рассмотренных и при соответствующем выборе параметров может быть сведена к любому предыдущему случаю. Предполагается, что имеется конечное число источников требований (l). Интенсивность каждого генератора требований – . Система содержит m обслуживающих приборов, каждый из которых характеризуется параметром . Наконец в системе имеется конечное число мест для ожидания, такое, что m+kl. Это приводит к следующему множеству параметров процесса гибели и размножения: 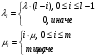 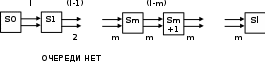 Обозначая /=, получим: 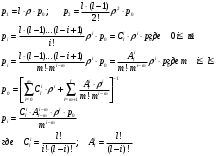 Среднее число занятых каналов: 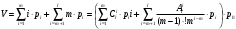 Так как каждый занятый канал обслуживает в среднем требований, то абсолютная пропускная способность: 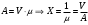 В СМО в среднем работает (l-N) источников, каждый из тех порождает поток : 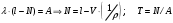 Среднее число требований, ожидающих обслуживание: Q=l-V  (1/+1); W=Q/A (1/+1); W=Q/AQ=N–V 8. Распределение числа требований в системе M/G/1/ Предположим, что все требования обслуживаются в порядке поступления. Установим связь между случайными величинами: 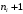 – число требований, остающихся в системе в момент ухода – число требований, остающихся в системе в момент уходатребования  ; ;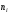 – число требований, остающихся в системе в момент ухода требования – число требований, остающихся в системе в момент ухода требования 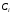 ; ;Рассмотрим два случая: Первый имеет место, когда уходящее требование не оставляет систему пустой, то есть 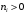 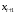 -время обслуживания -время обслуживания 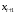 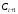 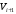 - число требований за - число требований за 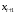 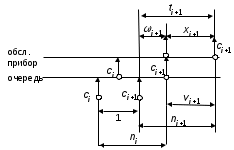 случай 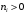 Так как требования 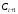 покидает систему покидает систему 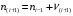 Второй случай имеет место, требование 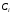 оставляет систему пустой, то есть оставляет систему пустой, то есть 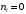 , тогда , тогда 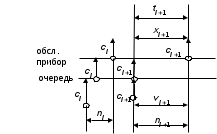 случай 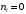 Обобщая оба случая, приходим к выводу, что система M/G/1 характеризуется равенством: 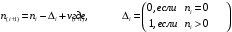 Определим производящую функцию случайной величины 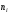 : :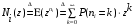 и производящую функцию предельной случайной величины 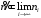 : :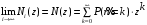 Образуем производящую функцию от полученного равенства 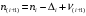 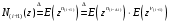 так как случайная величина 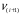 - число требований поступивших за - число требований поступивших за 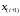 не зависит от 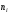 – число требований в системе в момент ухода требования – число требований в системе в момент ухода требования 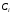 , ,тогда 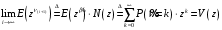 где 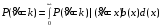 так как входящий поток – пуассоновский, то имеем: 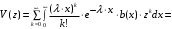 Меняя порядок операций суммирования и интегрирования, получаем: 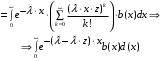 Так как 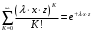 Определяем теперь преобразование Лапласа плотности времени обслуживания: 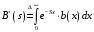 . .Сравнивая 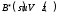 , получим важный результат: , получим важный результат: 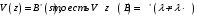 . .Преобразование Лапласа плотности вероятности времени обслуживания в точке 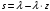 равно производящей функции распределения вероятностей числа требований за время одного обслуживания равно производящей функции распределения вероятностей числа требований за время одного обслуживания 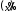 . .Итак: 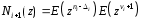 ; ;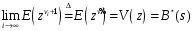 . .Теперь отдельно рассмотрим 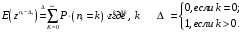 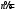 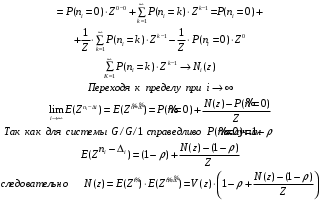 Решая относительно 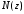 , получим первое уравнение Поллячика-Хинчина для преобразований: , получим первое уравнение Поллячика-Хинчина для преобразований: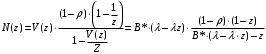 9. Распределение времени пребывания в системе M/G/1 Учитывая 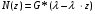 , первое уравнение Поллячика-Хинчина можно записать в виде: , первое уравнение Поллячика-Хинчина можно записать в виде: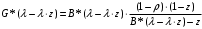 Введя замену переменной 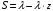 , имеем , имеем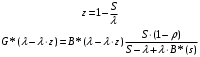 Это второе уравнение Поллячика-Хинчина для преобразований даёт выражение преобразования Лапласа распределения времени пребывания требования в системе. Так как 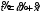 и учитывая, что и учитывая, что 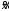 – время обслуживания требования не зависит от – время обслуживания требования не зависит от 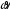 – времени ожидания этого требования в очереди и, что при сложении двух независимых случайных величин перемножаются преобразования Лапласа соответствующих функций распределения, получаем третье уравнение Поллячика–Хинчина для преобразования Лапласа распределения времени ожидания требования в очереди, то есть – времени ожидания этого требования в очереди и, что при сложении двух независимых случайных величин перемножаются преобразования Лапласа соответствующих функций распределения, получаем третье уравнение Поллячика–Хинчина для преобразования Лапласа распределения времени ожидания требования в очереди, то есть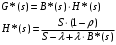 Различные производные производящей функции, вычисленные в точке z=1, дают возможность вычислить соответствующие моменты рассматриваемой случайной величины: 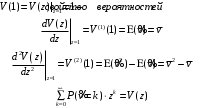 Точно также для непрерывных случайных величин можно найти моменты, вычисляя в точке 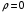 соответствующие производные преобразования Лапласа рассматриваемой случайной величины: соответствующие производные преобразования Лапласа рассматриваемой случайной величины: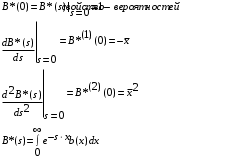 Используем теперь равенство для получения моментов случайной величены 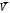 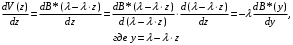 Полагая теперь 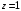 , то есть , то есть 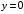 , имеем , имеем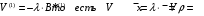 Мы получили хорошо обоснованное заключение о том, что ожидаемое число поступающих требований за время одного обслуживания равно 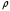 , что согласуется с полученными ранее результатом для G/G/1. , что согласуется с полученными ранее результатом для G/G/1.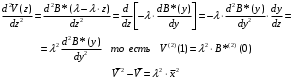 Уравнение Поллячика-Хинчина для преобразований позволяет найти моменты распределения числа требований в системе: 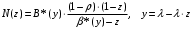 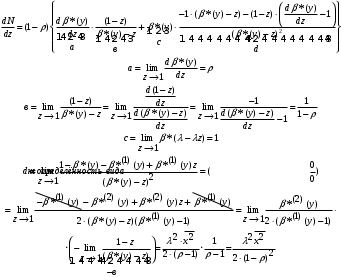 Дисперсия случайной величины x или второй центральный момент 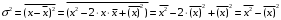 здесь: 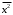 – второй начальный момент; – второй начальный момент;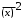 – квадрат первого начального момента; – квадрат первого начального момента;Если обозначить:  – нормированная дисперсия; – нормированная дисперсия;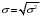 – стандарт; – стандарт;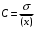 – коэффициент вариации; – коэффициент вариации;То учитывая: 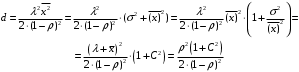 Это и есть результат, к которому мы стремились. Это выражение представляет собой среднее число преобразований в системе M/G/1, которое обычно называют формулой Поллячика - Хинчина для среднего значения. 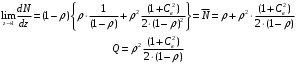 Среднее число преобразований в очереди  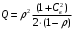 так как из анализа системы G/G/1 следует, что 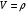 В качестве примера применения формулы Поллячика–Хинчина рассмотрим систему M/M/1 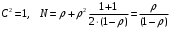 В качестве второго примера рассмотрим регулярное обслуживание, то есть систему M/D/1 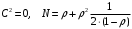 Таким образом, система типа М/D/1 содержит на 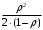 требований меньше, чем система М/М/1. требований меньше, чем система М/М/1.Для системы M/Er/1 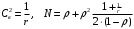 Это позволяет сделать вывод, что  Для системы G/G/m Кингман получил следующую оценку времени ожидания в очереди: 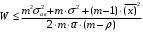 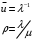 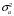 – дисперсия промежуточного интервала времени между прибытиями; – дисперсия промежуточного интервала времени между прибытиями;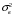 – дисперсия времени обслуживания; – дисперсия времени обслуживания;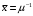 – математическое ожидание времени обслуживания; – математическое ожидание времени обслуживания;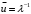 – математическое ожидание интервала между прибытиями; – математическое ожидание интервала между прибытиями;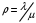 – коэффициент обслуживания – коэффициент обслуживанияЧисленные исследования показывают, что приближения ухудшается с увеличением 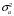 и и 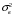 , и улучшается с увеличением , и улучшается с увеличением 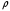 . .10.уравнение Поллячика–Хинчина для преобразования Лапласа в системе M/G/1 Учитывая 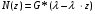 , первое уравнение Поллячика-Хинчина можно записать в виде: , первое уравнение Поллячика-Хинчина можно записать в виде: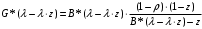 Введя замену переменной 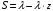 , имеем , имеем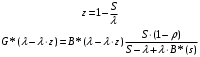 Это второе уравнение Поллячика-Хинчина для преобразований даёт выражение преобразования Лапласа распределения времени пребывания требования в системе. Так как 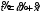 и учитывая и учитывая11. формула Поллячика - Хинчина для среднего значения в системе M/G/1 Учитывая 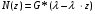 , первое уравнение Поллячика-Хинчина можно записать в виде: , первое уравнение Поллячика-Хинчина можно записать в виде: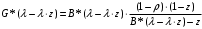 Введя замену переменной 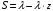 , имеем , имеем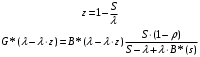 Это второе уравнение Поллячика-Хинчина для преобразований даёт выражение преобразования Лапласа распределения времени пребывания требования в системе. Так как 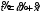 и учитывая, что и учитывая, что 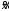 – время обслуживания требования не зависит от – время обслуживания требования не зависит от 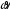 – времени ожидания этого требования в очереди и, что при сложении двух независимых случайных величин перемножаются преобразования Лапласа соответствующих функций распределения, получаем третье уравнение Поллячика–Хинчина для преобразования Лапласа распределения времени ожидания требования в очереди, то есть – времени ожидания этого требования в очереди и, что при сложении двух независимых случайных величин перемножаются преобразования Лапласа соответствующих функций распределения, получаем третье уравнение Поллячика–Хинчина для преобразования Лапласа распределения времени ожидания требования в очереди, то есть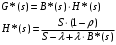 Различные производные производящей функции, вычисленные в точке z=1, дают возможность вычислить соответствующие моменты рассматриваемой случайной величины: 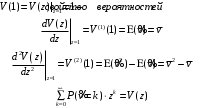 Точно также для непрерывных случайных величин можно найти моменты, вычисляя в точке 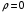 соответствующие производные преобразования Лапласа рассматриваемой случайной величины: соответствующие производные преобразования Лапласа рассматриваемой случайной величины: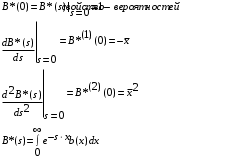 Используем теперь равенство для получения моментов случайной величены 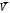 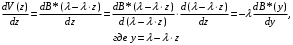 Полагая теперь 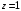 , то есть , то есть 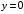 , имеем , имеем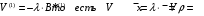 Мы получили хорошо обоснованное заключение о том, что ожидаемое число поступающих требований за время одного обслуживания равно 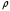 , что согласуется с полученными ранее результатом для G/G/1. , что согласуется с полученными ранее результатом для G/G/1.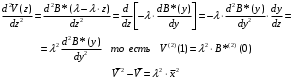 Уравнение Поллячика-Хинчина для преобразований позволяет найти моменты распределения числа требований в системе: 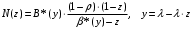 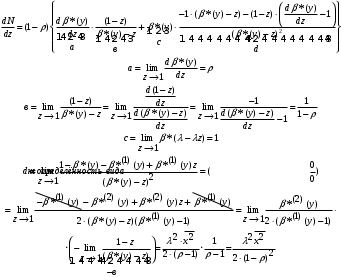 Дисперсия случайной величины x или второй центральный момент 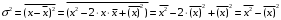 здесь: 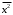 – второй начальный момент; – второй начальный момент;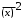 – квадрат первого начального момента; – квадрат первого начального момента;Если обозначить:  – нормированная дисперсия; – нормированная дисперсия;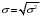 – стандарт; – стандарт;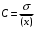 – коэффициент вариации; – коэффициент вариации;То учитывая: 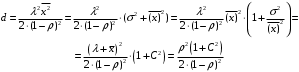 Это и есть результат, к которому мы стремились. Это выражение представляет собой среднее число преобразований в системе M/G/1, которое обычно называют формулой Поллячика - Хинчина для среднего значения. 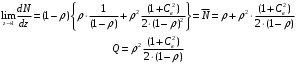 12. Теорема Бёрка (Burke) Р 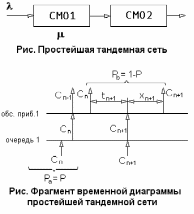 ассмотрим простейшую последовательную систему с двумя узлами, каждый из которых представляет СМО типа М/ М/1. ассмотрим простейшую последовательную систему с двумя узлами, каждый из которых представляет СМО типа М/ М/1.Фрагмент временной диаграммы для этой сети выглядит так, как это показано на рисунке слева. Пусть 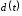 - плотность распределения вероятностей промежутков времени между последовательными требова-ниями на выходе, а - плотность распределения вероятностей промежутков времени между последовательными требова-ниями на выходе, а 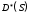 - преобразование Лапласа - преобразование Лапласа 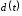 . Когда требование покидает узел 1, возможно одно из двух событий: . Когда требование покидает узел 1, возможно одно из двух событий:(a) в очереди имеется хотя бы одно требование (узел 1 не пуст) 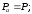 (b) в очереди нет требований (узел 1 пуст) 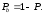 В первом случае - промежуток времени, через которое следующее требование покинет систему 1, распределен так же, как и время обслуживания: 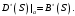 Во втором случае - промежуток времени, по истечении которого, следующее требование покинет систему, является суммой 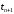 - времени до поступления следующего требования и - времени до поступления следующего требования и 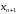 - времени обслуживания следующего требования. - времени обслуживания следующего требования.Так как эти два промежутка времени распределены независимо, то плотность распределения вероятностей их суммы равна свертке плотностей распределения суммируемых величин. Соответственно преобразование Лапласа плотности распределения: 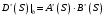 . .Так как промежуток времени между последовательными входящими требованиями является показательно распределенной случайной величиной, то 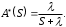 Кроме того, учитывая, что вероятность того, что требование покинет систему пустой, равна вероятности того, что поступающее требование застанет систему пустой и равна 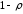 . Можно записать следующее безусловное преобразование Лапласа для плотности распределения промежутков времени между уходящими требованиями: . Можно записать следующее безусловное преобразование Лапласа для плотности распределения промежутков времени между уходящими требованиями: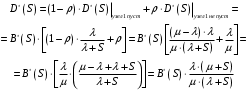 Учитывая, что время обслуживания – показательно распределенная случайная величина, то можно записать 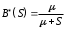 и, окончательно, имеем: и, окончательно, имеем: 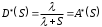 и, следовательно, распределение промежутков времени между уходящими требованиями, так же как и промежутки времени между поступающими требованиями, распределены по показательному закону с одним и тем же параметром. и, следовательно, распределение промежутков времени между уходящими требованиями, так же как и промежутки времени между поступающими требованиями, распределены по показательному закону с одним и тем же параметром.Этот результат, в 1956 году установленный Бёрк, справедлив и для СМО типа M/M/m. |
