вар 4. 1. Марковский процесс с дискретными состояниями и дискретным временем

• Название: 1. Марковский процесс с дискретными состояниями и дискретным временем
• Анкор: вар 4
• Дата: 11.10.2021
• Размер: 1.31 Mb.
• Имя файла: Answers.docx
• Тип: Документы; #245536
• страница: 4 из 4

18. Одноканальные замкнутые СМО (M/M/1/k/l).

Одноканальные замкнутые СМО (M/M/1/k/l).

Характерным для замкнутой системы массового обслуживания является наличие ограниченного числа источником заявок и, следовательно, интенсивность входного потока зависит от состояния самой системы.

В сущности, любая СМО имеет дело только с ограниченным числом источников заявок, но в ряде случаев число этих источников так велико, что можно пренебречь влиянием состояния СМО на поток заявок (АТС крупного города).

В замкнутой СМО источники заявок, наряду с каналами обслуживания, рассматриваются как элементы СМО.

Пусть m – число каналов обслуживания, l – число источников заявок, k – число мест в очереди (kl-1),  - интенсивность обслуживания.

S₀ – канал свободен

S₁ – канал занят, очереди нет

S_l – канал занят, в очереди l-1 требований

Из состояния S₀ в состояние S₁ систему переводит поток l, из S₁ в S₂ уже (l -1) , т. к. один источник заявок не функционирует и ожидает обслуживания. Из S₂ в S₃ в имеем поток (l -2)  и т. д.

kl-1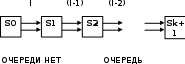



Пользуясь общим решением для схемы гибели и размножения, напишем: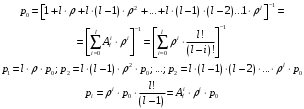



Относительная пропускная способность q=1, P_отн=0 т. к. каждое требование будет, в конце концов, обслужено.

P_зан=(1–p₀) – вероятность, что канал занят. Занятый канал обслуживает в среднем  требований в единицу времени, следовательно, абсолютная пропускная способность: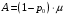



В СМО в среднем работает (l-N) источников заявок, каждый из которых поток интенсивность которого =.

Общий поток требований (l-N)  будет обслужен и, следовательно, равен абсолютной пропускной способности: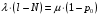



Откуда среднее число требований, находящихся в СМО: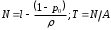



Значение N можно вычислить непосредственно: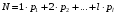



Среднее число требований, находящихся в обслуживающем устройстве равно: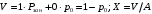



Среднее число требований, ожидающих обсл. в очереди: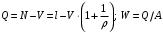



Эта система является саморегулируемой. Когда она перегружается, т. е. Образуется большая очередь, то интенсивность поступления дополнительных требований убывает.

Если kl-1



Пример. Система коллективного доступа реализует вычислительный процесс, обрабатывая запросы трех других периферийных систем обработки информации.

Определить эксплуатационные характеристики системы.

Решение.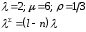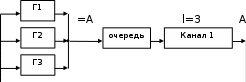







Вероятность занятости системы коллективного доступа: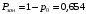



Абсолютная пропускная способность системы: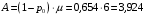



Среднее число запросов в системе: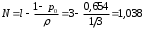



Среднее число требований в обслуживающем устройстве: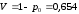



Среднее число требований в ожидающем устройстве: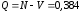



19.Многоканальная СМО с отказами (M/M/m/0)

Обозначения:

S₀ – все каналы свободны

S₁ – занят один канал, остальные свободны

---

S_i – занято i каналов

---

S_m – заняты все каналы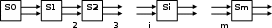



Пользуясь общим решением для схемы «гибели и размножения» получим формулы Эрланга: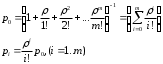



Зная все выражения можно найти характеристики эффективности СМО: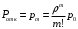



т. к. заявка получает отказ, если все каналы заняты.

Вероятность того, что заявка будет принята к обслуживанию (Она же относительная пропускная способность).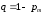



Абсолютная пропускная способность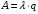



Среднее число заявок, находящихся в системе M/M/m/0 определим следующим образом:

A – среднее число заявок, обслуживаемых в единицу времени
 – среднее число заявок, обслуживаемых одним занятым каналом.

Тогда число занятых каналов (число заявок в системе).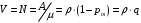



Однако N можно выразить и непосредственно:

N=0 p₀+1 p₁+…+m p_m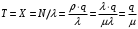



20.Одноканальная СМО с отказами (M/M/1/0) =16.

Пример.1

Сравнить эксплуатационные характеристики для моделей систем обработки информации M/M/2/k(k{0,3,})

=9^тр/_час 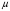=12^тр/_час

Решение:

=0,75 =0,375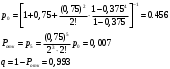



А=q=8,939 V=0,75q=0,745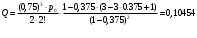



T=(0,745+0,104)/9=0,0943 час=5,65 мин

W=0,104/9=0,0115 час=0,69 мин

Х=0,745/9=0,083 час=4,96 мин

Модели	T	W	X	N	Q	V	q
M/M/2/	5,8	0,8	5	0,87	0,12	0,75	1
M/M/2/3	5,65	0,69	4,96	0,849	0,104	0,745	0,993
M/M/2/0	3,6	0	3,6	0,54	0	0,54	0,719

Пример 2.

Сравнить системы коллективного пользования с одним и двумя каналами обслуживания l=3, =2, =6.

Решение.

=¹/₃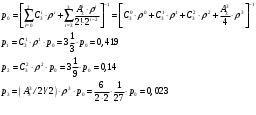






V=0,419+2(0,14+0,023)=0,744 – Среднее число занятых каналов

A=V=0,744·6=4,465 – Абсолютная пропускная способность

N=l-V/=3-0,744/(1/3)=0,767 – Среднее число тр. Вес.? (всего?)

Q=N-V=0,023 – Среднее число тр. в очереди

X=1/=0,167 T=N/A=0,172 W=0,005

Модели	T	W	X	N	Q	V	A	p0
M/M/2/k/3	0,172	0,005	0,167	0,767	0,023	0,744	4,465	0,419
M/M/1/k/3	0,265	0,098	0,167	1,038	0,384	0,654	3,923	0,346

Пример 3.

Вычислительная сеть M/D/1 обслуживает поток задач, запросы на выполнение которых поступают в случайные моменты времени (в среднем 9 требований в час). На решение одной задачи необходимо 5 минут.

Определить математическое ожидание:

Времени реакции системы на запрос –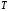

Времени ожидания в очереди –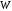

Числа требований в системе –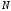

Числа требований в очереди –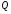

Числа требований в обслуживающем приборе –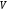

Если в качестве модели системы выбрать модель M/D/1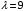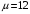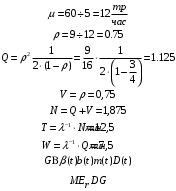

M/M/1	3	2,25	0,75	20	15	5
M/D/1	1,875	1,125	0,75	12,5	7,5	5
M/Er/1	2,438	1,688	0,75	16,25	11,25	5

Пример.4

Система обработки информации представима в виде M/M/1/0.

Интенсивность потока требований =9^тр/_час.
Средняя продолжительность обработки t_обр=5 мин.
Определить T, W, X, N, Q, V, q, A, P_отк.

Сравнить фактическую пропускную способность СМО с номинальной, которая была бы, если обработка информации длилась без перерыва.



Решение: Номинальная пропускная способность системы: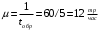



Относительная пропускная способность: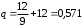



Таким образом, 57% заявок будет обслужено в установившемся режиме.

Вероятность отказа P_отк=1-q=0,429.

Значит около 49% требований получит отказ.

Абсолютная (фактическая) пропускная способность обслуживающего прибора (канала):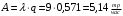

,

что почти вдвое меньше, чем номинальная пропускная способность, это объясняется случайным характером потока заявок и потока обслуживания.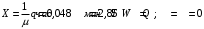



Пример 5.

Вычислительная система обслуживает поток задач. Входной поток и поток обслуживания простейшие.=9=12

Определить математическое ожидание

• 
  времени реакции системы на запрос – T
  
• 
  времени ожидания в очереди – W
  
• 
  числа требований в системе – N
  
• 
  числа требований в очереди – Q
  
• 
  числа требований в обслуживающем приборе – V
  
• 
  относительную пропускную способность – q
  

если в качестве модели системы выбрать модель M/M/1/3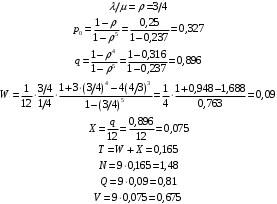





Пример 6 = Пример 5

Вычислительная система обслуживает поток задач. Входной поток и поток обслуживания простейшие.

=9

=12

Определить математическое ожидание

• 
  времени реакции системы на запрос – T
  
• 
  времени ожидания в очереди – W
  
• 
  числа требований в системе – N
  
• 
  числа требований в очереди – Q
  
• 
  числа требований в обслуживающем приборе – V
  
• 
  относительную пропускную способность – q
  

если в качестве модели системы выбрать модель M/M/1/3

Пример.7

Вычислительная система обслуживает поток задач. Входной поток и поток обслуживания простейшие.

=9

=12

Рассмотреть модель M/M/1/5 и сравнить характеристики для k₁=, k₂=3,k₃=1,k₄=0.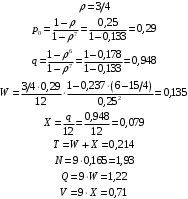

k	T	W	X	N	Q	V	q
	0,33	0,25	0,08	3	2,25	0,75	1
3	0,165	0,09	0,078	1,48	0,81	0,675	0,896
1	0,093	0,03	0,063	0,837	0,27	0,567	0,756
0	0,048	0	0,048	0,428	0	0,428	0,57

Пример 8.

Система коллективного доступа реализует вычислительный процесс, обрабатывая запросы трех других периферийных систем обработки информации.

Определить эксплуатационные характеристики системы.

Решение.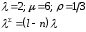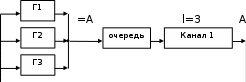







Вероятность занятости системы коллективного доступа: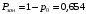



Абсолютная пропускная способность системы: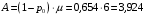



Среднее число запросов в системе: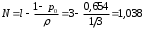



Среднее число требований в обслуживающем устройстве: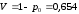



Среднее число требований в ожидающем устройстве: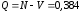



Пример.9

Систему обработки информации можно представить в виде модели M/M/2/0. Интенсивность требований l=9^тр/_час. Номинальная пропускная способность =12^тр/_час.

Найти эксплуатационные характеристики системы.

Решение. Приведенная интенсивность потока требований .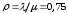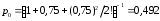



Вероятность отказа:

P_отк=p₂=(0,75)²/2!p₀=0,28p₀=0,138

Относительная и абсолютная пропускная способность:

q=1–p₂=0,862 A= q=7,754

Среднее число занятых каналов (заявок):

V=N= q=0,647

Среднее время пребывания требования в системе:

T=X=q/=0,018 час=4,3 мин

Модели	T	W	X	N	Q	V	q
M/M/2/	5,8	0,8	5	0,87	0,12	0,75	1
M/M/2/0	4,3	0	4,3	0,65	0	0,65	0,86
M/M/1/0	2,88	0	2,88	0,43	0	0,43	0,57