методы защиты информации. безопасность баз анных. 1. Математические (криптографические) методы защиты информации (ммзи) элемент системы инженернотехнической защиты информации Вопрос История криптографии

• Название: 1. Математические (криптографические) методы защиты информации (ммзи) элемент системы инженернотехнической защиты информации Вопрос История криптографии
• Анкор: методы защиты информации
• Дата: 26.04.2022
• Размер: 0.5 Mb.
• Имя файла: безопасность баз анных.docx
• Тип: Документы; #498660
• страница: 6 из 8

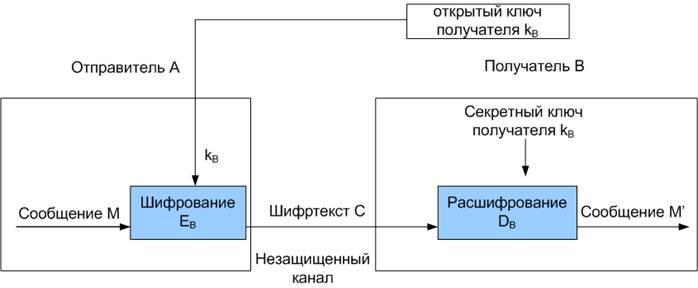
Тема 7. Асимметричные криптографические системы (криптосистемы с открытым ключом)

 

Цель:

Получить представление об асимметричных системах шифрования, математическом аппарате, лежащем в основе их функционирования, способах практического применения, сильными и слабыми сторонами, ознакомиться с основными стандартами открытых криптографических систем.

 

Задачи:

1. Изучить:

  принцип работы криптосистемы с открытым ключом;

  область применения асимметричных систем;

  достоинства и недостатки асимметричных криптосистем;

2. Приобрести компетенции:

  генерации открытых и закрытых ключей асимметричной криптосистемы;

  анализа и выбора криптографических систем для практического использования.

 

Содержание темы:

1. Понятие односторонней функции и односторонней функции с "лазейкой". Проблемы факторизации целых чисел.

2. Криптосистема RSA.

3. Достоинства и недостатки асимметричных систем шифрования.

 

Общие сведения об асимметричных криптосистемах (криптосистемах с открытым ключом)

 

Асимметричные криптографические системы были разработаны в 1970-х годах. Принципиальное отличие асимметричной криптосистемы от криптосистемы симметричного шифрования состоит в том, что для шифрования информации и ее последующего расшифрования используются различные ключи:

  открытый ключ К: используется для шифрования информации, вычисляется из секретного ключа k;

  секретный ключ k: используется для расшифрования информации, зашифрованной с помощью парного ему открытого ключа К.

 

Эти ключи различаются таким образом, что с помощью вычислений нельзя вывести секретный ключ k из открытого ключа К. Поэтому открытый ключ К может свободно передаваться по каналам связи.

Асимметричные системы называют еще двухключевыми криптографическими системами или криптосистемами с открытым ключом.

Обобщенная схема асимметричной криптосистемы шифрования с открытым ключом показана на рис. 12.

 



 

Рис. 12. Обобщенная схема асимметричной криптосистемы шифрования

 

Для криптографического закрытия и последующего расшифрования передаваемой информации используются открытый и секретный ключи получателя Всообщения. В качестве ключа зашифрования должен использоваться открытый ключ получателя, а в качестве ключа расшифрования - его секретный ключ.

Секретный и открытый ключи генерируются попарно. Секретный ключ должен оставаться у его владельца; он должен быть надежно защищен от несанкционированного доступа (аналогично ключу шифрования в симметричных алгоритмах). Копия открытого ключа должна иметься у каждого абонента криптографической сети, с которым обменивается информацией владелец секретного ключа. Процесс передачи зашифрованной информации в асимметричной криптосистеме осуществляется следующим образом:

1.Подготовительный этап.

Абонент Вгенерирует пару ключей: секретный ключ k_Bи открытый ключ К_В. Открытый ключ К_Впосылается абоненту А и остальным абонентам (или делается доступным, например, на разделяемом ресурсе).

2.Использование - обмен информацией между абонентами Аи В. Абонент А зашифровывает сообщение с помощью открытого ключа К_Вабонента Ви отправляет шифртекст абоненту В.

 

Абонент В расшифровывает сообщение с помощью своего секретного ключа k_B. Никто другой (в том числе абонент А) не может расшифровать данное сообщение, так как не имеет секретного ключа абонента В. Защита информации в асимметричной криптосистеме основана на секретности ключа k_Bполучателя сообщения.

Отметим характерные особенности асимметричных криптосистем:

1.   Открытый ключ К_Ви криптограмма Смогут быть отправлены по незащищенным каналам, то есть противнику известны К_Ви С.

2.   Алгоритмы шифрования и расшифрования:

1)  Е_В : М → С,

2)  D_B: С → М.

являются открытыми.

 

У. Диффи и М. Хеллман сформулировали требования, выполнение которых обеспечивает безопасность асимметричной криптосистемы:

1.  Вычисление пары ключей (К_В, k_B) получателем Вна основе начального условия должно быть простым.

2.  Отправитель А, зная открытый ключ К_Ви сообщение М, может легко вычислить криптограмму:

1)    С=Е_КВ(М).

3.  Получатель В, используя секретный ключ k_Bи криптограмму С, может легко восстановить исходное сообщение:

1)    M = D_kВ(C).

 

4.  Противник, зная открытый ключ К_В, при попытке вычислить секретный ключ k_Bнаталкивается на непреодолимую вычислительную проблему.

5. Противник, зная пару (К_В, С), при попытке вычислить исходное сообщение Мнаталкивается на непреодолимую вычислительную проблему.

 

Вопрос 1. Понятие односторонней функции и односторонней функции с "лазейкой" (с секретом) Проблемы факторизации целых чисел.

 

Концепция асимметричных криптографических систем с открытым ключом основана на применении однонаправленных функций.

Неформально однонаправленную функцию можно определить следующим образом. Пусть Xи Y- некоторые произвольные множества. Функция f:X→Yявляется однонаправленной, если для всех хпринадлежит Xможно легко вычислить функцию:

 

у =f(x),гдеyпринадлежитY.

 

И в то же время для большинства у принадлежащих Y достаточно сложно получить значение х принадлежащее X, такое, что f(x) = у(при этом полагают, что существует по крайней мере одно такое значение х.

Основным критерием отнесения функции к классу однонаправленных функций является отсутствие эффективных алгоритмов обратного преобразования Y →X.

В качестве примера однонаправленной функции можно указать целочисленное умножение. Прямая задача - вычисление произведения двух очень больших целых чисел Р и Q, то есть нахождение значения:

 

N=PxQ

 

является относительно несложной задачей для компьютера.

 

Обратная задача - факторизация, или разложение на множители большого целого числа, то есть нахождение делителей Ри Qбольшого целого числа N=Р х Qявляется практически неразрешимой задачей при достаточно больших значениях N. По современным оценкам теории чисел, при целом N = 2⁶⁶⁴иР Q для разложения числа N потребуется около 10²³ операций, то есть задача практически неразрешима для современных компьютеров.

Другой характерный пример однонаправленной функции - это модульная экспонента с фиксированными основанием и модулем. Пусть Аи N - целые числа, такие, что 1 < А < N.Определим множество Z_N:

 

Z_N={0, 1,2, ... N - 1}.

 

Тогда модульная экспонента с основанием А по модулю N представляет собой функцию:

 

f_a.n-:Z_N →Z_N

f_a.n {x)= A^x(modN),

 

где X - целое число, 1 < х < N - 1.

 

Существуют эффективные алгоритмы, позволяющие достаточно быстро вычислить значения функции f_a.n {x).

Если у = А^х, то естественно записать х = log_A(y).

Поэтому задачу обращения функции f_a._n(x) называют задачей нахождения дискретного логарифма, или задачей дискретного логарифмирования.

Задача дискретного логарифмирования формулируется следующим образом. Для известных целых A, N, у найти целое число х, такое, что:

 

A^хmod N = у.

 

Алгоритм вычисления дискретного логарифма за приемлемое время пока не найден. Поэтому модульная экспонента считается однонаправленной функцией. По современным оценкам теории чисел, при целых числах А = 2⁶⁶⁴ и N= 2⁶⁶⁴ решение задачи дискретного логарифмирования (нахождение показателя степени х для известного у) потребует около 10²⁶ операций, то есть эта задача имеет в 10³ раз большую вычислительную сложность, чем задача разложения на множители. При увеличении длины чисел разница в оценках сложности задач возрастает.

Следует отметить, что пока не удалось доказать невозможность существования эффективного алгоритма вычисления дискретного логарифма за приемлемое время. Исходя из этого модульная экспонента отнесена к однонаправленным функциям условно, что, однако, не мешает с успехом применять ее на практике.

Вторым важным классом функций, используемых при построении криптосистем с открытым ключом, являются так называемые однонаправленные функции с секретом. Дадим неформальное определение такой функции. Функция

 

f:X→Y

 

относится к классу однонаправленных функций с секретом в том случае, если она является однонаправленной и, кроме того, возможно эффективное вычисление обратной функции, если известен секрет (секретное число, строка или другая информация, ассоциируемая с данной функцией).

В качестве примера однонаправленной функции с секретом можно указать используемую в криптосистеме RSA модульную экспоненту с фиксированными модулем и показателем степени. Переменное основание модульной экспоненты используется для представления числового значения сообщения М либо криптограммы.

Как и в случае симметричных криптографических систем, с помощью асимметричных криптосистем обеспечивается не только конфиденциальность, но также подлинность и целостность передаваемой информации. Подлинность и целостность любого сообщения обеспечивается формированием цифровой подписи этого сообщения и отправкой в зашифрованном виде сообщения вместе с цифровой подписью. Проверка соответствия подписи полученному сообщению после его предварительного расшифровывания представляет собой проверку целостности и подлинности принятого сообщения.

 

Вопрос 2. Криптосистема RSA.

 

Криптоалгоритм RSA предложили в 1978 году три автора: Р. Райвест (Rivest), А. Шамир (Shamir) и А. Адлеман (Adleman). Алгоритм получил свое название по первым буквам фамилий его авторов. Алгоритм RSA стал первым алгоритмом с открытым ключом, который может работать в режиме как шифрования данных, так и электронной цифровой подписи.

Надежность алгоритма RSA основывается на трудности факторизации больших чисел и сложности вычисления дискретных логарифмов в конечном поле.

В алгоритме RSA открытый ключ К_В, секретный ключ k_B, сообщение Ми криптограмма С принадлежат множеству целых чисел:

 

Z_N ={0, 1,2, ...,N- 1},

 

где N - модуль:

 

N = PxQ.

 

Здесь Р и Q - случайные большие простые числа. Для обеспечения максимальной безопасности выбирают Р и Qравной длины и хранят в секрете.

Множество Z_Nс операциями сложения и умножения по модулю Nобразует арифметику по модулю N.

Открытый ключ К_Ввыбирают случайным образом так, чтобы выполнялись следующие условия:

 

1 < К_B ≤ φ (N), НОД(К_В, φ (N) = 1,

φ (N) = (P- l)(Q-1),

 

где φ (N)- функция Эйлера.

 

Функция Эйлера φ (N) указывает количество положительных целых чисел в интервале от 1 до N, которые взаимно просты с N.

Второе из указанных выше условий означает, что открытый ключ К_ви функция Эйлера φ (N) должны быть взаимно простыми.

Далее, используя расширенный алгоритм Евклида, вычисляют секретный ключ k_B, такой, что:

 

k_Bx K_B≡l(mod φ (N))

 

или

 

k_B = K_B^-1(mod (Р-1)(Q-1)).

 

Это можно осуществить, так как получатель В знает пару простых чисел (Р, Q) и может легко найти φ(N). Заметим, что k_Bи N должны быть взаимно простыми.

Открытый ключ К_Bиспользуют для шифрования данных, а секретный ключ k_B -для расшифрования.

Процедура шифрования определяет криптограмму С через пару (открытый ключ К_B, сообщение М) в соответствии со следующей формулой:

 

C = E_KB(M) = M^KB(modN).

 

В качестве алгоритма быстрого вычисления значения С используют ряд последовательных возведений в квадрат целого М и умножений на М с приведением по модулю N.

Расшифрование криптограммы С выполняют, используя пару (секретный ключ k_B, криптограмма С) по следующей формуле:

 

M = D_kB (C) = C^kB(modN).

 

Процедуры шифрования и расшифрования в алгоритме RSA рассмотрим на примере шифрования сообщения CAB. Для простоты вычислений будут использоваться небольшие числа. На практике применяются очень большие числа (длиной 250-300 десятичных разрядов).

Действия пользователяВ:

1. Выбирает Р=3 и Q=11.

2. Вычисляет модуль N=Р х Q=Зх11=33.

3. Вычисляет значение функции Эйлера для N = 33:

 

φ (N) = φ (33) = (Р- 1)(Q- 1) = 2 х 10 = 20.

 

Выбирает в качестве открытого ключа К_Впроизвольное число с учетом выполнения условий:

 

1<К_В< 20, НОД (К_В, 20) = 1.

 

Пусть К_В= 7.

Вычисляет значение секретного ключа k_B, используя расширенный алгоритм Евклида при решении сравнения

k_B = 7^-1(mod 20) или

К_В хk_B mod(Р- 1)(Q- 1) =1.

Решение дает k_B = 3.

4. Пересылает пользователю А пару чисел (N=33,K_B = 7).

Действия пользователя А:

5.   Представляет шифруемое сообщение как последовательность целых чисел в диапазоне 0-32. Пусть буква А представляется как число 1, буква В - как число 2, буква С - как число 3. Тогда сообщение CAB можно представить как последовательность чисел 312, то есть М₁ = 3, М₂= 1, М₃= 2.

6.   Шифрует текст, представленный в виде последовательности чисел М_и М₂ и М₃, используя ключ К_в= 7 и N = 33, по формуле:

 

С_i = M_i^KB (mod N) = M_i⁷(mod 33).

 

Получает:

С₁= 3⁷(mod 33) = 2187(mod 33) = 9,

С₂ = l⁷(mod 33) = l(mod 33) = 1,

С₃ = 2⁷(mod 33) = 128(mod 33) = 29.

 

Отправляет пользователю В криптограмму:

 

С₁ С₂, С₃= 9, 1, 29.

 

Действия пользователя В:

7.   Расшифровывает принятую криптограмму С₁ С₂, С₃, используя секретный ключ k_B= 3, по формуле:

 

Мi = C_i^KB(mod N) = C_i³(mod 33).

 

Получает:

М₁ = 9³(mod 33) = 729(mod 33) = 3,

М₂ = l³(mod 33) = l(mod 33) = 1,

М₃= 29³(mod 33) - 24389(mod 33) = 2.

 

Таким образом, восстановлено исходное сообщение CAB: 312.

Криптоалгоритм RSA всесторонне исследован и признан стойким при достаточной длине ключей. В настоящее время длина ключа 1024 бит считается приемлемым вариантом. Некоторые авторы утверждают, что с ростом мощности процессоров криптоалгоритм RSA потеряет стойкость к атаке полного перебора. Однако увеличение мощности процессоров позволит применять более длинные ключи, что повышает стойкость RSA Следует отметить, что алгоритм RSA можно применять как для шифрования сообщений, так и для электронной цифровой подписи.

Нетрудно видеть, что в асимметричной криптосистеме RSA количество используемых ключей связано с количеством абонентов линейной зависимостью (в системе из N пользователей используется 2 х N ключей), а не квадратической, как в симметричных системах.

 

Вопрос 3. Достоинства и недостатки асимметричных систем шифрования.

 

Асимметричные криптографические системы обладают следующими важными преимуществами перед симметричными криптосистемами:

     в асимметричных криптосистемах решена сложная проблема распределения ключей между пользователями, так как каждый пользователь может сгенерировать свою пару ключей сам, а открытые ключи пользователей могут свободно публиковаться и распространяться по сетевым коммуникациям;

     исчезает квадратическая зависимость числа ключей от числа пользователей; в асимметричной криптосистеме количество используемых ключей связано с количеством абонентов линейной зависимостью (в системе из N пользователей используется 2N ключей), а не квадратической, как в симметричных системах;

     асимметричные криптосистемы позволяют реализовать протоколы взаимодействия сторон, которые не доверяют друг другу, поскольку при использовании асимметричных криптосистем закрытый ключ должен быть известен только его владельцу.

 

Однако у асимметричных криптосистем существуют и недостатки:

     на настоящий момент нет математического доказательства необратимости используемых в асимметричных алгоритмах функций;

     по сравнению с симметричным шифрованием, асимметричное существенно медленнее, поскольку при шифровании и расшифровке используются весьма ресурсоемкие операции. По этой же причине реализовать аппаратный шифратор с асимметричным алгоритмом существенно сложнее, чем аппаратно симметричный алгоритм;

     необходимо защищать открытые ключи от подмены.

 

Перечень литературы и Интернет-ресурсов:

1. А.П.Алферов, А.Ю.Зубов, А.С.Кузьмин, А.В.Черемушкин. Основы криптографии: Учебное пособие. – М.: Гелиос АРВ, 2005. стр. 59-69.

2. В.М. Фомичев. Дискретная математика и криптология Курс лекций. – М.: ДИАЛОГ-МИФИ, 2003. стр. 143-150.

3. Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. – М.: ДМК Пресс, 2008. стр. 154-162.

4. http://www.fstec.ru/

5. http://www.cryptopro.ru/