методы защиты информации. безопасность баз анных. 1. Математические (криптографические) методы защиты информации (ммзи) элемент системы инженернотехнической защиты информации Вопрос История криптографии

• Название: 1. Математические (криптографические) методы защиты информации (ммзи) элемент системы инженернотехнической защиты информации Вопрос История криптографии
• Анкор: методы защиты информации
• Дата: 26.04.2022
• Размер: 0.5 Mb.
• Имя файла: безопасность баз анных.docx
• Тип: Документы; #498660
• страница: 3 из 8

Тема 3. Криптосистема и её основные составляющие

 

Цель:

Рассмотреть криптосистему, как совокупность взаимосвязанных элементов, совместное функционирование которых обеспечивает защиту информации. Получить представление об основных критериях классификации шифров.

 

Задачи:

1. Изучить:

     основные элементы криптосистемы, их функциональное назначение;

     принципы работы блочных и поточных шифров, достоинства и недостатки;

     предназначение, способы генерации и использования ключей;

     требования к криптосистемам и шифрам.

2. Приобрести компетенции:

     классификации и выбора криптоалгоритма для практического использования;

     оценки эффективности криптоалгоритма, с точки зрения общепринятых требований.

 

Содержание темы:

1. Понятие криптосистемы.

2. Блочные и поточные шифры.

3. Ключевая система шифра.

4. Основные требования к шифрам.

 

Вопрос 1. Понятие криптосистемы.

 

В настоящие время вместо понятия шифра используется понятие криптографической системы с секретным ключом, которая задается следующими пятью компонентами:

1. M- пространство открытых текстов;

2. C - пространство шифрованных текстов;

3. K - пространство ключей;

4. E_k ( k  K ) множество преобразований зашифрования:

 

E_k : M → C (k K)

 

5. Dk (k  K) - множество преобразований расшифрования:

 

D_k : C → M (k K)

 

Преобразования E_kи D_k для всех (k  K) и любого открытого текста mM должны удовлетворять условию:

 

Dk [Ek (m)] = m

 

Обобщенная схема криптосистемы шифрования показана на рис. 6. Исходный текст передаваемого сообщения (или хранимой информации) М зашифровывается с помощью криптографического преобразования Е_k1 с получением в результате шифртекста С:

 

С = E_k1(М),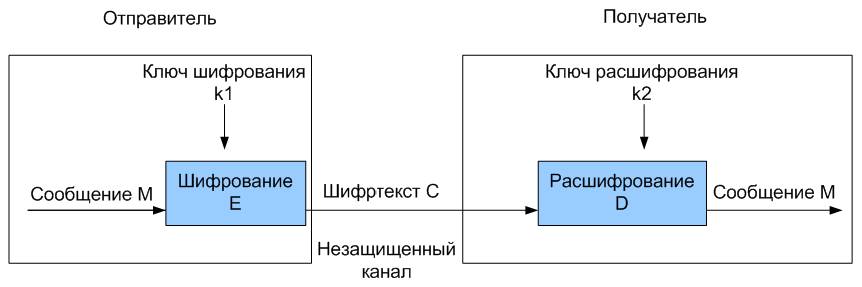

 



 

Рис. 6. Обобщенная схема криптосистемы шифрования

 

где k₁ — параметр функции Е, называемый ключом шифрования.

 

Шифртекст С, называемый еще криптограммой, содержит исходную информацию М в полном объеме, однако последовательность знаков в нем внешне представляется случайной и не позволяет восстановить исходную информацию без знания ключа шифрования k₁.

Ключ шифрования является тем элементом, с помощью которого можно варьировать результат криптографического преобразования. Данный элемент может принадлежать конкретному пользователю или группе пользователей и являться для них уникальным. Зашифрованная с использованием конкретного ключа информация может быть расшифрована только его владельцем (или владельцами).

Обратное преобразование информации выглядит следующим образом:

 

М’ = D_k2(С).

 

Функция D является обратной к функции Е и производит расшифрование шифртекста. Она также имеет дополнительный параметр в виде ключа k₂. Ключ расшифрования k₂ должен однозначно соответствовать ключу k₁, в этом случае полученное в результате расшифрования сообщение М будет эквивалентно М. При отсутствии верного ключа k₂ получить исходное сообщение М’ = М с помощью функции D невозможно.

Преобразование шифрования может быть симметричным или асимметричным относительно преобразования расшифрования. Соответственно, различают два основных класса криптосистем:

  симметричные криптосистемы;

  асимметричные криптосистемы.

 

Известно несколько классификаций криптографических алгоритмов. Одна из них подразделяет КА в зависимости от числа ключей, применяемых в конкретном алгоритме:

  бесключевые КА - не используют в вычислениях никаких ключей;

  одноключевые КА - работают с одним ключевым параметром (секретным ключом);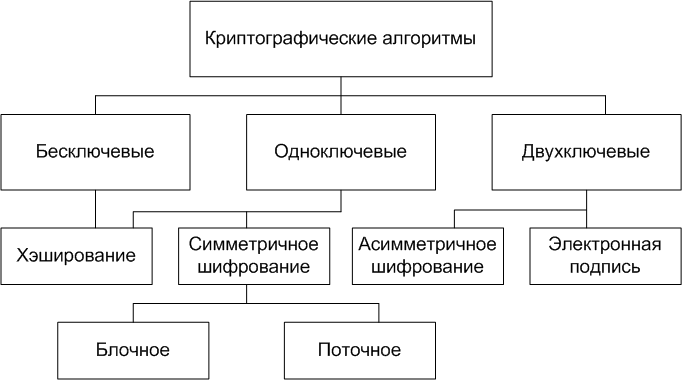

 



 

Рис. 7. Классификация криптографических алгоритмов

 

        двухключевые КА - на различных стадиях работы в них применяются два ключевых параметра: секретный и открытый ключи.

 

Существуют более детальные классификации, например, показанная на рис. 7.

 

Согласно основному правилу Керкгоффса множества Ek и Dk могут быть известны не только криптографу, но и криптоаналитику. Секретность же сообщения обеспечивается сокрытием того факта, какое именно преобразование из известного множества используется для зашифрования.

Современные криптосистемы с секретным ключом подразделяются на блочные и потоковые (поточные).

 

Вопрос 2. Блочные и поточные системы.

 

Блочное шифрование характеризуется тем, что информация предварительно разбивается на блоки фиксированной длины (например, 64 или 128 бит). При этом в различных криптографических алгоритмах или даже в разных режимах работы одного и того же алгоритма блоки могут шифроваться как независимо друг от друга, так и «со сцеплением» - когда результат шифрования текущего блока данных зависит от значения предыдущего блока или от результата шифрования предыдущего блока.

Блочные шифры являются той основой, на которой реализованы практически все симметричные криптосистемы. Симметричные криптосистемы позволяют кодировать и декодировать файлы произвольной длины. Практически все алгоритмы используют для преобразований определенный набор обратимых математических преобразований.

Методика создания цепочек из зашифрованных блочными алгоритмами байтов позволяет шифровать ими пакеты информации неограниченной длины. Отсутствие статистической корреляции между битами выходного потока блочного шифра используется для вычисления контрольных сумм пакетов данных и в хэшировании паролей. На сегодняшний день разработано достаточно много стойких блочных шифров.

Криптоалгоритм считается идеально стойким, если для прочтения зашифрованного блока данных необходим перебор всех возможных ключей до тех пор, пока расшифрованное сообщение не окажется осмысленным. В общем случае стойкость блочного шифра зависит только от длины ключа и возрастает экспоненциально с ее ростом.

К. Шеннон предложил для получения стойких блочных шифров использовать два общих принципа: рассеивание и перемешивание.

Рассеивание представляет собой распространение влияния одного знака открытого текста на много знаков шифртекста, что позволяет скрыть статистические свойства открытого текста.

Перемешивание предполагает использование таких шифрующих преобразований, которые усложняют восстановление взаимосвязи статистических свойств открытого и шифрованного текстов. Однако шифр должен не только затруднять раскрытие, но и обеспечивать легкость зашифрования и расшифрования при известном пользователю секретном ключе.

Распространенным способом достижения эффектов рассеивания и перемешивания является использование составного шифра, то есть такого шифра, который может быть  реализован в виде некоторой последовательности простых шифров, каждый из которых вносит свой вклад в значительное суммарное рассеивание и перемешивание.

В составных шифрах в качестве простых шифров чаще всего используются простые перестановки и подстановки. При перестановке просто перемешивают символы открытого текста, причем конкретный вид перемешивания определяется секретным ключом. При подстановке каждый символ открытого текста заменяют другим символом из того же алфавита, а конкретный вид подстановки также определяется секретным ключом. Следует заметить, что в современном блочном шифре блоки открытого текста и шифртекста представляют собой двоичные последовательности обычно длиной 64 или 128 бит. При длине 64 бит каждый блок может принимать 2⁶⁴значений. Поэтому подстановки выполняются в очень большом алфавите, содержащем до 2⁶⁴ = 10¹⁹ «символов».

При многократном чередовании простых перестановок и подстановок, управляемых достаточно длинным секретным ключом, можно получить стойкий шифр с хорошим рассеиванием и перемешиванием.

Все действия, производимые блочным криптоалгоритмом над данными, основаны на том факте, что преобразуемый блок может быть представлен в виде целого неотрицательного числа из диапазона, соответствующего его разрядности. Например, 32-битовый блок данных можно интерпретировать как число из диапазона 0-4294 967 295. Кроме того, блок, разрядность которого представляет собой «степень двойки», можно трактовать как сцепление нескольких независимых неотрицательных чисел из меньшего диапазона (указанный выше 32-битовый блок можно также представить в виде сцепления двух независимых 16-битовых чисел из диапазона 0-65 535 или в виде сцепления четырех независимых 8-битовых чисел из диапазона 0-255).

Характерным признаком блочных алгоритмов является многократное и косвенное использование материала ключа. Это определяется в первую очередь требованием невозможности обратного декодирования в отношении ключа при известных исходном и зашифрованном текстах. Для решения этой задачи в приведенных выше преобразованиях чаще всего используется не само значение ключа или его части, а некоторая, иногда необратимая функция от материала ключа. Более того, в подобных преобразованиях один и тот же блок или элемент ключа используется многократно. Это позволяет при выполнении условия обратимости функции относительно величины X сделать функцию необратимой относительно ключа К.

 

В шифрах потока (поточных шифрах) шифрование делается в один момент времени над одним символом (таким, как буква или бит). Пусть имеется поток исходного текста, поток зашифрованного текста и поток ключей. Обозначим исходный поток Р, поток зашифрованного текста – С и поток ключей – К. Тогда работу поточной криптосистемы можно формализовать следующим образом:

 

Р = Р₁Р₂Р₃,…

С = С₁С₂С₃,….

К = (k₁,k₂,k₃)

C1 = E_k1(P₁),

C₂ = E_k2(P₂),

C3 = E_k3(P₃)…

 

Символы исходного текста принимаются алгоритмом шифрования по одному. Символы зашифрованного текста также создаются по одному в один и тот же момент времени. Ключевой поток может быть определен многими способами. Это может быть только одно значение, используемое алгоритмом. Значения могут зависеть от исходного текста или символов зашифрованного текста. Значения могут также зависеть от предыдущих ключевых значений.

Потоковые криптосистемы широко используются в военных и других системах близких к ним по назначению для шифрования данных и преобразованных в цифровую форму речевых сигналов. Это связано, прежде всего, с относительной простотой конструирования и реализации генераторов псевдослучайных, шифрующих последовательностей на базе теории линейных рекуррентных последовательностей над конечными полями и других математических дисциплин. Однако главным фактором такого применения поточных криптосистем является отсутствие размножения ошибок. Так как при передаче данных и речевых сообщений в стратегической связи используются каналы недостаточно высокого качества, то любая криптосистема, которая увеличивает и без того нередкие ошибки, неприменима. Кроме указанных приложений поточные криптосистемы используются и при передаче данных в локальных и глобальных сетях ЭВМ, где их непрерывное действие препятствует эффективному криптоанализу.

Главное свойство блочных криптосистем состоит в том, что каждый бит текста шифровки является функцией почти всех бит соответствующего блока открытого текста, и никакие два блока открытого текста не могут быть представлены одним и тем же блоком шифротекста. Основное их преимущество состоит в том, что даже небольшие изменения открытого текста или ключа вызывают большие и непредсказуемые изменения в шифротексте. Однако существенным их недостатком является распространение (размножение) ошибки внутри блока. Результатом изменения одного бита в принятом блоке будет неправильное расшифрование всего блока.

Возможно образование комбинированных криптосистем поточного и блочного типа с использованием лучших свойств каждой из них. В таких системах поточное шифрование комбинируется с перестановками бит в блоках. Открытый текст сначала шифруется на основе шифра замены, а затем полученный шифротекст разбивается на блоки фиксированного размера и в каждом блоке дополнительно реализуется под управлением ключа шифр перестановки. В результате получается шифр, не размножающий ошибки, в котором неизвестно, какому биту открытого текста соответствует бит шифровки, что существенно повышает стойкость криптосистемы.

 

Вопрос 3. Ключевая система шифра.

 

Ключ— это важнейший компонент шифра, отвечающий за выбор преобразования, применяемого для зашифрования конкретного сообщения. Обычно ключ представляет собой некоторую буквенную или числовую последовательность.

Эта последовательность как бы "настраивает" алгоритм шифрования. Ключ шифрования является тем элементом, с помощью которого можно варьировать результат криптографического преобразования. Данный элемент может принадлежать конкретному пользователю или группе пользователей и являться для них уникальным. Зашифрованная с использованием конкретного ключа информация может быть расшифрована только его владельцем (или владельцами).

В целом при построении шифров могут использоваться ключи разных типов: долговременные, суточные и сеансовые (для передачи каждого конкретного сообщения).

Более детально характеристики ключей (ключевых систем) будут рассмотрены ниже для каждой криптосистемы.

 

Вопрос 4. Основные требования к шифрам и криптосистемам.

 

При проведении любой криптоатаки обычно пользуются общепринятым в криптографии правилом Керкгоффса. В книге «Военная криптография», изданной в 1883 г., он сформулировал шесть следующих требований к системам шифрования:

1) система должна быть нераскрываемой, если не теоретически, то практически;

2) компрометация системы не должна причинять неудобств ее пользователям;

3) секретный ключ должен быть легко запоминаемым без каких-либо записей;

4) криптограмма должна быть представлена в такой форме, чтобы ее можно было передать по телеграфу;

5) аппаратура шифрования должна быть портативной и такой, чтобы ее мог обслуживать один человек;

6) система должна быть простой. Она не должна требовать ни запоминания длинного перечня правил, ни большого умственного напряжения.

 

Второе из этих правил и стало называться правилом Керкгоффса. Суть его состоит в том, что при проведении криптоанализа можно считать известной систему шифрования. Стойкость (или надежность) шифрования должна определяться лишь секретностью ключа шифрования.

 

Для современных криптографических систем защиты информации сформулированы следующие общепринятые требования:

      зашифрованное сообщение должно поддаваться чтению только при наличии ключа;

      число операций, необходимых для определения использованного ключа шифрования по фрагменту шифрованного сообщения и соответствующего ему открытого текста, должно быть не меньше общего числа возможных ключей;

      число операций, необходимых для расшифровывания информации путем перебора всевозможных ключей должно иметь строгую нижнюю оценку и выходить за пределы возможностей современных компьютеров (с учетом возможности использования сетевых вычислений);

      знание алгоритма шифрования не должно влиять на надежность защиты;

      незначительное изменение ключа должно приводить к существенному изменению вида зашифрованного сообщения даже при использовании одного и того же ключа;

      структурные элементы алгоритма шифрования должны быть неизменными;

      дополнительные биты, вводимые в сообщение в процессе шифрования, должен быть полностью и надежно скрыты в шифрованном тексте;

      длина шифрованного текста должна быть равной длине исходного текста;

      не должно быть простых и легко устанавливаемых зависимостью между ключами, последовательно используемыми в процессе шифрования;

      любой ключ из множества возможных должен обеспечивать надежную защиту информации;

      алгоритм должен допускать как программную, так и аппаратную реализацию, при этом изменение длины ключа не должно вести к качественному ухудшению алгоритма шифрования.

 

Перечень литературы и Интернет-ресурсов:

1. А.П. Алферов, А.Ю. Зубов, А.С. Кузьмин, А.В. Черемушкин. Основы криптографии: Учебное пособие. – М.: Гелиос АРВ, 2005. стр. 32-39.

2. В.М. Фомичев. Дискретная математика и криптология Курс лекций. – М.: ДИАЛОГ-МИФИ, 2003. стр. 115-121.

3. Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. – М.: ДМК Пресс, 2008. стр. 122-131.

4. http://www.fstec.ru/

5. http://www.cryptopro.ru/