методы защиты информации. безопасность баз анных. 1. Математические (криптографические) методы защиты информации (ммзи) элемент системы инженернотехнической защиты информации Вопрос История криптографии
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
Тема 2. Характеристика информационных ресурсов, подлежащих криптографической защите Цель: Рассмотреть информацию, как объект защиты. Определить основные параметры информации, способы оценки этих параметров с точки зрения криптографической защиты. Задачи: 1. Изучить: основные математические модели информационных ресурсов; особенности формализации речевой информации; принципы формирования количественных характеристик сообщения. 2. Приобрести компетенции: использования критериев оценки информационных ресурсов построения частотных характеристик сообщений. Содержание темы: 1. Виды информации, подлежащие закрытию, их модели и свойства. 2. Частотные характеристики открытых сообщений. 3. Критерии на открытый текст. 4. Особенности нетекстовых сообщений. Вопрос 1. Виды информации, подлежащие закрытию, их модели и свойства. Математическая модель шифра содержит вероятностные распределения Р(Х) и Р(К) на множествах открытых текстов и ключей соответственно. Если Р(К) определяется свойствами устройств, служащих для генерации ключей (которые могут быть случайными или псевдослучайными), то Р(Х) определяется частотными характеристиками самих текстов, подлежащих шифрованию. Характер таких текстов может быть различный: это могут быть обычные литературные тексты, формализованные данные межмашинного обмена и т. д. Так или иначе, открытые тексты обладают многими закономерностями, некоторые из которых наследуются шифрованными текстами. Именно это является определяющим фактором, влияющим на надежность шифрования. Потребность в математических моделях открытого текста продиктована, прежде всего, следующими соображениями. Во-первых, даже при отсутствии ограничений на временные и материальные затраты по выявлению закономерностей, имеющих место в открытых текстах, нельзя гарантировать того, что такие свойства указаны с достаточной полнотой. Например, хорошо известно, что частотные свойства текстов в значительной степени зависят от их характера. Поэтому при математических исследованиях свойств шифров прибегают к упрощающему моделированию, в частности, реальный открытый текст заменяется его моделью, отражающей наиболее важные его свойства. Во-вторых, при автоматизации методов криптоанализа, связанных с перебором ключей, требуется "научить" ЭВМ отличать открытый текст от случайной последовательности знаков. Ясно, что соответствующий критерий может выявить лишь адекватность последовательности знаков некоторой модели открытого текста. Модели открытого текста более высоких приближений учитывают зависимость каждого знака от большего числа предыдущих знаков. Ясно, что, чем выше степень приближения, тем более "читаемыми" являются соответствующие модели. Проводились эксперименты по моделированию открытых текстов с помощью ЭВМ. Вопрос 2. Частотные характеристики открытых сообщений. Криптография занимается защитой сообщений, содержащихся на некотором материальном носителе. При этом сами сообщения представляют собой последовательности знаков (или слова) некоторого алфавита. Различают естественные алфавиты, например русский или английский, и специальные алфавиты (цифровые, буквенно-цифровые), например двоичный алфавит, состоящий из символов 0 и 1. В свою очередь, естественные алфавиты также могут отличаться друг от друга даже для данного языка. Наиболее привычны буквенные алфавиты, например русский, английский и т. д. Приведем сведения об алфавитах некоторых естественных европейских языков. Полный русский алфавит состоит из 33 букв: А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я Вместе с тем используются и сокращенные русские алфавиты, содержащие 32, 31 или 30 букв. Можно отождествить буквы Е и Ё, И и Й, Ь и Ъ. Часто бывает удобно включить в алфавит знак пробела между словами, в качестве которого можно взять, например, символ #. Английский алфавит состоит из 26 букв: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Иногда используется сокращенный 25-буквенный алфавит, в котором отождествлены буквы I и J. В вычислительной технике распространены 128-битовые и 256-битовые алфавиты, использующие представление знаков алфавита в виде 7- или 8-значных двоичных комбинаций. Таблица 1.
Наиболее известен код ASCII (American Standart Code for Information Interchange) — американский стандартный код информационного обмена. Фрагмент этого кода приведен в Таблице 1. В практике передачи сообщений по техническим каналам связи используется множество других кодов, основанных на двоичном кодировании. Буквенный алфавит, в котором буквы расположены в их естественном порядке, обычно называют нормальным алфавитом. В противном случае говорят о смешанных алфавитах. В свою очередь, смешанные алфавиты делят на систематически перемешанные алфавиты и случайные алфавиты. К первым относят алфавиты, полученные из нормального на основе некоторого правила, ко вторым — алфавиты, буквы которых следуют друг за другом в хаотическом (или случайном) порядке. Криптоанализ любого шифра невозможен без учета особенностей текстов сообщений, подлежащих шифрованию. Глубинные закономерности текстовых сообщений исследуются в теории информации. Наиболее важной для криптографии характеристикой текстов является избыточность текста, введенная К. Шенноном. Именно избыточность открытого текста, проникающая в шифртекст, является основной слабостью шифра. Более простыми характеристиками текстов, используемыми в криптоанализе, являются такие характеристики, как повторяемость букв, пар букв (биграмм) и вообще т-ок (т-грамм), сочетаемость букв друг с другом, чередование гласных и согласных и некоторые другие. Такие характеристики изучаются на основе эмпирических наблюдений текстов достаточно большой длины. Для установления статистических закономерностей проводилась большая серия экспериментов по оценке вероятностей появления в открытом тексте фиксированных m-грамм (для небольших значений m). Таблица 2.
В Таблице 2 приведена частота букв (в процентах) ряда европейских языков. Некоторая разница значений частот в приводимых в различных источниках таблицах объясняется тем обстоятельством, что частоты существенно зависят не только от длины текста, но и от его характера. Так, в технических текстах редкая буква Ф может стать довольно частой в связи с частым использованием таких слов, как функция, дифференциал, диффузия, коэффициент и т. п. Еще большие отклонения от нормы в частоте употребления отдельных букв наблюдаются в некоторых художественных произведениях, особенно в стихах. Поэтому для надежного определения средней частоты буквы желательно иметь набор различных текстов, заимствованных из различных источников. Вместе с тем, как правило, подобные отклонения незначительны, и в первом приближении ими можно пренебречь. В связи с этим подобные таблицы, используемые в криптографии, должны составляться с учетом характера переписки. 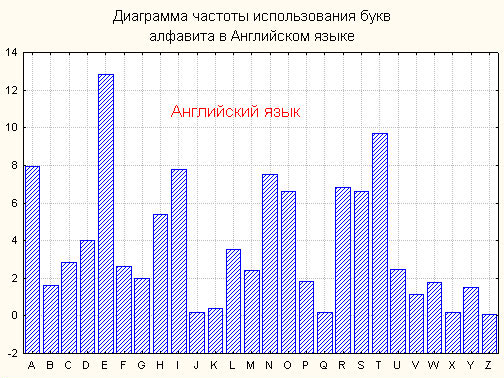 Рис. 1. Частоты букв английского языка (в процентах) Наглядное представление о частотах букв дает диаграмма встречаемости. Так, для английского языка, в соответствии с табл. 2, такая диаграмма изображена на рис. 1. Для русского языка частоты (в порядке убывания) знаков алфавита, в котором отождествлены Е с Ё, Ь с Ъ, а также имеется знак пробела (-) между словами, приведены в Таблице 3. Таблица 3.
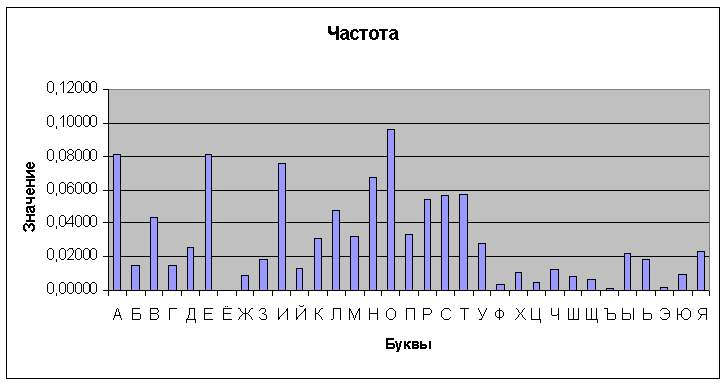 Рис. 2. Диаграмма частот букв русского языка 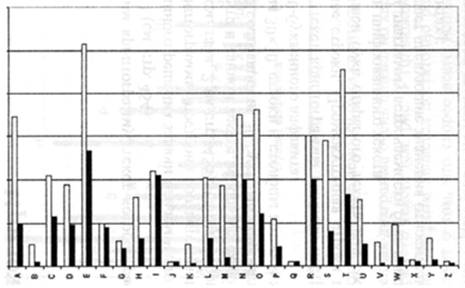 Рис. 3. Частоты символов ASCII (буквы) (светлым — в статье по компьютерной тематике; темным — в тексте программы на языке Паскаль) На основании табл. 3 получаем следующую диаграмму частот. Имеется мнемоническое правило запоминания десяти наиболее частых букв русского алфавита. Эти буквы составляют нелепое слово СЕНОВАЛИТР. Можно также предложить аналогичный способ запоминания частых букв английского языка, например, с помощью слова TETRIS-HONDA Приведенные выше закономерности имеют место для обычных "читаемых" открытых текстов, используемых при общении людей. Как уже отмечалось ранее, эти закономерности играют большую роль в криптоанализе. В частности, они используются при построении формализованных критериев на открытый текст, позволяющих применять методы математической статистики в задаче распознавания открытого текста в потоке сообщений. При использовании же специальных алфавитов требуются аналогичные исследования частотных характеристик "открытых текстов", возникающих, например, при межмашинном обмене информацией или в системах передачи данных. В этих случаях построение формализо-ванных критериев на "открытый текст" — задача значительно более сложная. В качестве примера приведем частотные характеристики букв английского алфавита, входящих в состав кода ASCII. Помимо криптографии частотные характеристики открытых сообщений существенно используются и в других сферах. Например, клавиатура компьютера, пишущей машинки или линотипа — это замечательное воплощение идеи ускорения набора текста, связанное с оптимизацией расположения букв алфавита относительно друг друга в зависимости от частоты их применения. Вопрос 3. Критерии на открытый текст. Заменив реальный открытый текст его моделью, мы можем теперь построить критерий распознавания открытого текста. При этом можно воспользоваться либо стандартными методами различения статистических гипотез, либо наличием в открытых текстах некоторых запретов, таких, например, как биграмма ЪЪ в русском тексте. Проиллюстрируем первый подход при распознавании позначной модели открытого текста. Итак, согласно нашей договоренности, открытый текст представляет собой реализацию независимых испытаний случайной величины, значениями которой являются буквы алфавита А = {ах,...,ап}, появляющиеся в соответствии с распределением вероятностей Р(А) = (р(ах),...,р(ап)). Требуется определить, является ли случайная последовательность схс2...с, букв алфавита А открытым текстом или нет. Пусть Н0 — гипотеза, состоящая в том, что данная последовательность — открытый текст, Н1 — альтернативная гипотеза. В простейшем случае последовательность c1c2...ct можно рассматривать при гипотезе Н1 как случайную и равновероятную. Эта альтернатива отвечает субъективному представлению о том, что при расшифровании криптограммы с помощью ложного ключа получается «бессмысленная» последовательность знаков. В более общем случае можно считать, что при гипотезе Н, последовательность c1c2...cs представляет собой реализацию независимых испытаний некоторой случайной величины, значениями которой являются буквы алфавита А = {ах,...,ап}, появляющиеся в соответствии с распределением вероятностей Q(A)i = (q(ax),..., q(an)). При таких договоренностях можно применить, например, наиболее мощный критерий различения двух простых гипотез, который дает лемма Неймана-Пирсона. В силу своего вероятностного характера такой критерий может совершать ошибки двух родов. Критерий может принять открытый текст за случайный набор знаков. Такая ошибка обычно называется ошибкой первого рода, ее вероятность равна а = P{Н1/Н0}. Аналогично вводится ошибка второго рода и ее вероятность b = P{Н0/Н1}. Эти ошибки определяют качество работы критерия. В криптографических исследованиях естественно минимизировать вероятность ошибки первого рода, чтобы не «пропустить» открытый текст. Лемма Неймана-Пирсона при заданной вероятности первого рода минимизирует также вероятность ошибки второго рода. Критерии на открытый текст, использующие запретные сочетания знаков, например к-граммы подряд идущих букв, будем называть критериями запретных к -грамм. Они устроены чрезвычайно просто. Отбирается некоторое число 5 редких к-грамм, которые объявляются запретными. Теперь, просматривая последовательно к -грамму за к-граммой анализируемой последовательности c1,c2…ci, мы объявляем ее случайной, как только в ней встретится одна из запретных к - грамм, и открытым текстом в противном случае. Такие критерии также могут совершать ошибки в принятии решения. В простейших случаях их можно рассчитать. Несмотря на свою простоту, критерии запретных к -грамм являются весьма эффективными. Вопрос 4. Особенности нетекстовых сообщений. Существуют два класса систем связи: цифровые и аналоговые. Все наши предыдущие исследования были связаны с цифровыми сигналами, то есть сигналами, имеющими конечное число дискретных уровней. Аналоговые сигналы являются непрерывными. Типичным примером такого сигнала является речевой сигнал, передаваемый по обычному телефону. Информацию, передаваемую аналоговыми сигналами, также необходимо защищать, в том числе и криптографическими методами. Имеются два различных способа шифрования речевого сигнала. Первый состоит в перемешивании (скремблировании) сигнала некоторым образом. Это делается путем изменения соотношений между временем, амплитудой и частотой, не выводящих за пределы используемого диапазона. Второй способ состоит в преобразовании сигнала в цифровую форму, к которой применимы обычные методы дискретного шифрования. Зашифрованное сообщение далее передается по каналу с помощью модема. После расшифрования полученной криптограммы вновь восстанавливается аналоговая форма сигнала. Прежде чем перейти к деталям, необходимо остановиться на некоторых особенностях речевых сигналов.  Рис. 4. Непрерывные сигналы характеризуются своим спектром. Спектр сигнала — это эквивалентный ему набор синусоидальных составляющих (называемых также гармониками или частотными составляющими). Спектр сигнала получается разложением функции, выражающей зависимость формы сигнала от времени, в ряд Фурье. Спектр периодического сигнала— линейчатый (дискретный), он состоит из гармоник с кратными частотами. Спектр непериодического сигнала — непрерывный. Типичный спектр речевого сигнала показан на рис. 4. Частотные составляющие в диапазонах 3-4 кГц и менее 300 Гц быстро убывают. Таким образом, очень высокие частотные компоненты имеют существенно меньший вклад в сигнал, чем частоты в диапазоне 500-3000 Гц. Если ограничиться частотами, не превышающими 3 кГц, и использовать высокочувствительный анализатор, то спектр, производимый некоторыми звуками, имеет вид зубчатой кривой приблизительно следующего вида (см. рис. 5). Мы видим несколько пиков графика, называемых формантами. 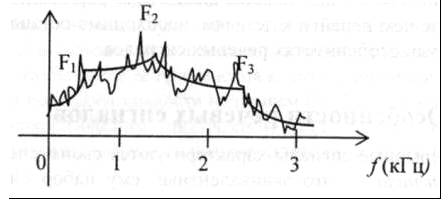 Рис. 5. Речевой сигнал является переносчиком смысловой информации. Эта информация при прослушивании речевого сигнала может быть записана в виде текста сообщения. Слуховое восприятие речевого сигнала более богато и несет как основную текстовую информацию, так и дополнительную в виде ударений и интонаций. Элементарными единицами слуховой информации являются элементарные звуки — фонемы, а смысловыми единицами — звучащие слоги, слова и фразы. Для каждого языка имеется свой набор фонем. Например, в русском и английском языках имеется около 40 фонем. Множество фонем разбивается на три класса. Гласные образуют одно семейство, согласные и некоторые другие фонетические звуки (для английского языка — это, например, звуки ch, sh) образуют два класса, называемые взрывными звуками и фрикативными звуками. Гласные производятся движением голосовых связок под воздействием потоков воздуха. Проходя через гортань, они превращаются в серию вибраций. Затем воздушный поток проходит через некоторое число резонаторов, главными из которых являются нос, рот и горло, превращаясь в воспринимаемые человеческим ухом фонемы. Возникающие звуки зависят от формы и размеров этих резонаторов, но в значительной степени они характеризуются низкочастотными составляющими. Гласные звуки производятся в течение длительного времени. Как правило, требуется около 100 мс для достижения его пиковой амплитуды. Взрывные звуки производятся путем «перекрытия» воздушного потока с последующим его выпусканием с взрывным эффектом. Блокирование воздушного потока может осуществляться различными способами — языком, нёбом или губами. Например, звук «п» произносится при блокировании воздушного потока губами. Взрывные звуки характеризуются их высокочастотными составляющими. До 90% их пиков амплитуды имеют длительность, не превышающую 5 мсек. Фрикативные звуки производятся частичным перекрытием воздушного потока, что дает звук, похожий на «белый шум». Этот звук затем фильтруется резонаторами голосового тракта. Фрикативный звук обычно богат пиками амплитуды длительностью 20-50 мс и сконцентрирован по частоте от 1 до 3 кГц. Пример фрикатива — звук «ссс...». Другой важной характеристикой человеческой речи является частота основного тона. Это — частота вибраций голосовых связок. Среднее значение этой частоты колеблется у разных людей, и у каждого говорящего имеется отклонение в пределах октавы выше или ниже этой центральной частоты. Обычно у мужчины частота основного тона колеблется около 1300 Гц, у женщины она выше. Речевые сигналы не только передают информацию, но и дают сведения о голосовых характеристиках говорящего, что позволяет идентифицировать его по голосу. Можно использовать высоту, форманты, временную диаграмму и другие характеристики речевого сигнала, чтобы попытаться сформировать сигнал, схожий с оригиналом. Это воспроизведение может быть в некоторой степени неестественным, и некоторые индивидуальные характеристики говорящего будут утеряны. Перечень литературы и Интернет-ресурсов: 1. А.П. Алферов, А.Ю. Зубов, А.С. Кузьмин, А.В. Черемушкин. Основы криптографии: Учебное пособие. – М.: Гелиос АРВ, 2005. стр. 25-32. 2. В.М. Фомичев. Дискретная математика и криптология. Курс лекций. – М.: ДИАЛОГ-МИФИ, 2003. стр. 110-115. 3. Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. – М.: ДМК Пресс, 2008. стр. 117-122. 4. http://www.fstec.ru/ 5. http://www.cryptopro.ru/ |
