методы защиты информации. безопасность баз анных. 1. Математические (криптографические) методы защиты информации (ммзи) элемент системы инженернотехнической защиты информации Вопрос История криптографии
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
Тема 5. Имитостойкость шифров Цель: Рассмотреть имитостойкость, как характеристику шифра наиболее полно отражающую способность криптосистемы противостоять наиболее опасным атакам со стороны неавторизованных лиц, а также методы обеспечения имитостойкости. Задачи: 1. Изучить: формы и способы действий неавторизованных лиц направленных на нарушение целостности и достоверности информации; параметры, характеризующие имитостойкость криптосистемы; методы обеспечения различных уровней имитостойкости. 2. Приобрести компетенции: обеспечения совершенной (идеальной) имитостойкости; выбора и использования основных методов обеспечения имитостойкости криптосистемы. Содержание темы: 1. Имитация и подмена сообщения. 2. Характеристики имитостойкости. 3. Методы обеспечения имитостойкости шифров. 4. Совершенная имитостойкость. Коды аутентификации. Вопрос 1. Имитация и подмена сообщения. Целостность данных обеспечивается присоединением к передаваемым данным специального кода (имитовставки), вырабатываемой по секретному ключу. Имитовставка является разновидностью контрольной суммы, то есть некоторой эталонной характеристикой сообщения, по которой осуществляется проверка целостности последнего. Алгоритм формирования имитовставки должен обеспечивать ее зависимость по некоторому сложному криптографическому закону от каждого бита сообщения. Проверка целостности сообщения выполняется получателем сообщения путем выработки по секретному ключу имитовставки, соответствующей полученному сообщению, и ее сравнения с полученным значением имитовставки. При совпадении делается вывод о том, что информация не была модифицирована на пути от отправителя к получателю. Вопрос 2. Характеристики имитостойкости. Помимо пассивных действий со стороны потенциального противника, состоящих в подслушивании или перехвате передаваемой по каналу связи шифрованной информации, возможны также его активные действия, состоящие в попытках подмены или имитации сообщения. Если передается шифрованное сообщение у принадлежащее Y (полученное из открытого текста х принадлежащего X на ключе к принадлежащего К ), то противник может его заменить на у', отличный от у . При этом он будет рассчитывать на то, что на действующем ключе к новая криптограмма при расшифровании будет воспринята как некий осмысленный открытый текст х', отличный от х. Конечно, это событие может произойти с некоторой вероятностью, и чем больше эта вероятность, тем успешнее будет попытка подмены. 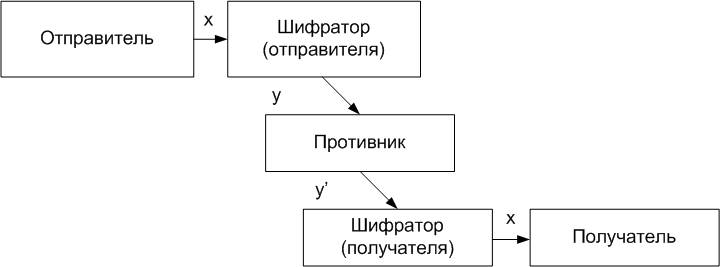 Рис. 8. Попытка имитации может быть предпринята противником в том случае, когда линия связи готова к работе (на приеме и передаче установлены действующие ключи), но в рассматриваемый момент никакого сообщения не передается. В таком случае противник может выбрать некий у, принадлежащий Y и послать его от имени законного отправителя. При этом он будет рассчитывать на то, что на действующем ключе его криптограмма при расшифровании будет воспринята как некий осмысленный открытый текст. Чем больше вероятность этого события, тем успешнее будет попытка имитации. При теоретическом исследовании активных действий противника, его обычно ставят в наиболее благоприятные условия, помещая между отправителем и получателем, см. рис. 8. Имитостойкость шифра определяется, как его способность противостоять попыткам противника по имитации или подмене сообщения. Вопрос 3. Методы обеспечения имитостойкости шифров. Наряду с конфиденциальностью не менее важной задачей является обеспечение целостности информации, другими словами, — неизменности ее в процессе передачи или хранении. Решение этой задачи предполагает разработку средств, позволяющих обнаруживать не столько случайные искажения (для этой цели вполне подходят методы теории кодирования с обнаружением и исправлением ошибок), сколько целенаправленное навязывание противником ложной информации. Для этого в передаваемую информацию вносится избыточность. Как правило, это достигается добавлением к сообщению некоторой проверочной комбинации, вычисляемой с помощью специального алгоритма и играющей роль контрольной суммы для проверки целостности полученного сообщения. Главное отличие такого метода от методов теории кодирования состоит в том, что алгоритм выработки проверочной комбинации является "криптографическим", то есть зависящим от секретного ключа. Без знания секретного ключа вероятность успешного навязывания противником искаженной или ложной информации мала. Такая вероятность служит мерой имитостойкости шифра, то есть способности самого шифра противостоять активным атакам со стороны противника. Итак, для проверки целостности к сообщению М добавляется проверочная комбинация S, называемая кодом аутентичности сообщения (сокращенно — КАС), или имитовставкой. В этом случае по каналу связи передается пара С = (М, S) . При получении сообщения М пользователь вычисляет значение проверочной комбинации и сравнивает его с полученным контрольным значением S. Несовпадение говорит о том, что данные были изменены. Как правило, код аутентичности сообщения является значением некоторой (зависящей от секретного ключа) криптографической хэш-функции от данного сообщения: hk(M) = S . К ключевым хэш-функциям предъявляются определенные требования. К ним относятся: невозможность вычисления значения hk(M) = S для заданного сообщения М без знания ключа к; невозможность подбора для заданного сообщения М с известным значением hk(M) = S другого сообщения Мх с известным значением hk (М,) = 5, без знания ключа к. Первое требование направлено против создания поддельных (сфабрикованных) сообщений при атаках типа имитация; второе — против модификации передаваемых сообщений при атаках типа подмена. Еще один способ борьбы с атаками типа повтор состоит в модификации исходного сообщения посредством добавления некоторой уникальной информации: например, порядкового номера сообщения. Использование данного способа представлено на рис. 9. 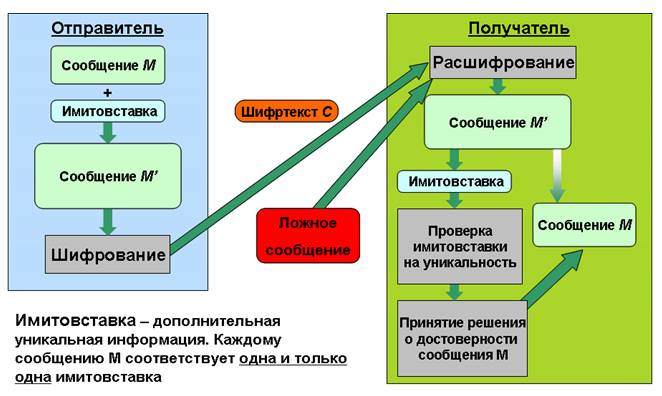 Рис. 9. Вопрос 4. Совершенная имитостойкость. Коды аутентификации. Коды аутентификации сообщений (Message authentication codes или MACs) — это следующий базисный элемент, о котором мы поговорим. Они не обеспечивают секретность, но гарантируют аутентификацию и целостность. Они дают уверенность, что сообщение пришло именно от того человека, который обозначен как автор (это аутентификация), и что сообщение по пути не изменилось (а это целостность). Вы можете рассматривать MAC как защищающую от вскрытия оболочку сообщения. Кто угодно может прочесть сообщение — оболочка не обеспечивает секретность. Но кто-то, кто знает ключ MAC, может удостовериться, что сообщение не было изменено. Конкретнее, MAC — это номер, который прикреплен к цифровому сообщению. Для MAC применяют секретные ключи совместного использования, типа симметричных алгоритмов шифрования. Сначала абонент А договаривается о ключе с абонентом Б. Затем, когда она хочет послать абоненту Б сообщение, она вычисляет MAC сообщения (применяя секретный ключ) и присваивает его сообщению. У каждого сообщения есть уникальный MAC для любого возможного ключа. Когда абонент Б получает сообщение, он вычисляет его MAC (опять-таки используя все тот же совместный ключ) и сравнивает его с тем значением MAC, которое прислал абонент А. Если они совпадают, то он может быть уверен в двух вещах: сообщение действительно пришло от абонента А (или от кого-то, кто знает секрет общего ключа) — потому что только применяя этот ключ, можно вычислить MAC, и это сообщение цельное и не измененное — так как MAC можно вычислить только по полному и точному сообщению. Если бы противник прослушивал связь, он смог бы прочитать сообщение. Однако если бы он попытался изменить текст сообщения или MAC, то вычисленный абонентом MAC не был бы равен тому значению, которое он получил. Противнику пришлось бы изменить сообщение, а затем изменить MAC, чтобы он был правильным для нового сообщения, но она не могла бы этого сделать, так как не знает ключа. Банки используют такую простую систему аутентификации уже несколько десятилетий. Абонент А может прибегнуть к той же уловке, чтобы установить подлинность информации, содержащейся в базе данных. Добавляя информацию в базу данных, он вычисляет MAC и хранит его вместе с информацией. Когда он извлекает информацию, то снова вычисляет MAC и сравнивает его с тем значением, которое хранилось в базе данных. Если они совпадают, то он приобретает уверенность, что никто не изменил информацию. MAC постоянно используются в Интернете. Их применяют, например, в протоколе IPsec, чтобы гарантировать, что IP-пакеты не были изменены в промежутке между отправлением и прибытием на место назначения. Их используют во всевозможных протоколах межбанковских переводов для установления подлинности сообщений. Большинство MAC сконструированы с применением симметричных алгоритмов или односторонних хэш-функций. Например, в СВС-МАС применяется симметричный алгоритм, а в НМАС и NMAC — хэш-функции. Кодирование одноразового использования — это самый простой из всех алгоритмов, его изобрели незадолго до XX века. Основная идея его состоит в том, что у вас есть набор символов ключа. Вы прибавляете один символ ключа к каждому символу открытого текста и никогда не повторяете символы ключа. (Это «одноразовая» часть.) Например, вы прибавляете В (2) к С (3), чтобы получить Е (5), или Т (20) к L (12), чтобы получить F (6). ((20 + 12) mod 26 = 6.) Такая система подходит для любого алфавита, в том числе и бинарного. И это единственный имеющийся у нас алгоритм, безопасность которого может быть доказана. Вспомним понятие расстояния уникальности. Оно возрастает при увеличении длины ключа. Когда длина ключа приближается к длине сообщения, расстояние уникальности стремится к бесконечности. Это означает, что невозможно восстановить открытый текст, и это доказывает безопасность одноразового кодирования. Но, с другой стороны, это практически бесполезно. Поскольку ключ должен при этом быть такой же длины, как и сообщение, то проблема не решена. Единственный здравый подход к шифрованию должен предполагать, что очень длинная секретная информация — сообщение — превращается с его помощью в очень короткую секретную информацию — ключ. При помощи одноразового кодирования вы нисколько не сокращаете секретную информацию. Так же сложно доставить шифр получателю, как и доставить само сообщение. Современная криптография зашифровывает большие объекты, например цифровые фильмы, соединения через Интернет или телефонные разговоры, и такое шифрование практически невозможно осуществить, работая с одноразовым кодированием. Если утверждают, что некая программа использует этот алгоритм, то здесь почти наверняка обман. А если и нет, то программа наверняка непригодна для использования или небезопасна. Перечень литературы и Интернет-ресурсов: 1. А.П. Алферов, А.Ю. Зубов, А.С. Кузьмин, А.В. Черемушкин. Основы криптографии: Учебное пособие. – М.: Гелиос АРВ, 2005. стр. 45-52. 2. В.М. Фомичев. Дискретная математика и криптология Курс лекций. – М.: ДИАЛОГ-МИФИ, 2003. стр. 128-135. 3. Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. – М.: ДМК Пресс, 2008. стр. 140-147. 4. http://www.fstec.ru/ 5. http://www.cryptopro.ru/ Тема 6. Практическая реализация симметричных криптографических алгоритмов Цель: Получить представление о симметричных системах шифрования, математическом аппарате, лежащем в основе их функционирования, способах практического применения, сильными и слабыми сторонами, ознакомиться с основными стандартами симметричных криптографических систем. Задачи: 1. Изучить: принцип работы симметричной криптосистемы; область применения симметричных систем; достоинства и недостатки симметричных криптосистем; 2. Приобрести компетенции: оценки исходных сообщений на предмет криптографического преобразования с использованием симметричных систем; анализа и выбора криптографических систем для практического использования. Содержание темы: 1. Криптографические стандарты. DES, AES. 2. Алгоритм шифрования данных, определяемый ГОСТ 28147-89. 3. Достоинства и недостатки симметричных систем шифрования. Вопрос 1. Криптографические стандарты. DES, AES. Алгоритм шифрования данных DES (Data Encryption Standard) был опубликован в 1977 году. Блочный симметричный алгоритм DES остается пока распространенным алгоритмом, используемым в системах защиты коммерческой информации. Алгоритм DES состоит из чередующейся последовательности перестановок и подстановок. Алгоритм DES осуществляет шифрование 64-битовых блоков данных с помощью 64-битового ключа, в котором значащими являются 56 бит (остальные 8 бит - проверочные биты для контроля на четность). Обобщенная схема процесса шифрования в блочном алгоритме DES показана на рис. 10. 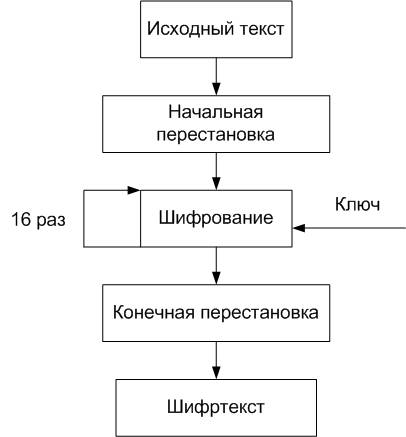 Рис. 10. Обобщенная схема шифрования в алгоритме DES Процесс шифрования заключается в начальной перестановке битов 64-битового блока, шестнадцати циклах (раундах) шифрования и, в заключение, в конечной перестановке битов. Расшифрование в DES является операцией, обратной шифрованию, и выполняется путем повторения операций шифрования в обратной последовательности. Основные достоинства алгоритма DES: используется только один ключ длиной 56 бит; относительная простота алгоритма обеспечивает высокую скорость обработки; зашифровав сообщение с помощью одного пакета программ, для расшифровки можно использовать любой другой пакет программ, соответствующий алгоритму DES; криптостойкость алгоритма вполне достаточна для обеспечения информационной безопасности большинства коммерческих приложений. Современная микропроцессорная техника позволяет уже сегодня за достаточно приемлемое время взламывать симметричные блочные шифры с длиной ключа 40 бит. Для такого взламывания используется метод полного перебора - тотального опробования всех возможных значений ключа (метод «грубой силы»). Сегодня все шире используются два современных криптостойких алгоритма шифрования: отечественный стандарт шифрования ГОСТ 28147-89 и новый криптостандарт США - AES (Advanced Encryption Standard). Алгоритм AES не похож на большинство известных алгоритмов симметричного шифрования, структура которых носит название сети Фейстеля и аналогична российскому ГОСТ 28147-89. В отличие от отечественного стандарта шифрования, алгоритм AES представляет каждый блок обрабатываемых данных в виде двухмерного байтового массива размером 4x4, 4x6 или 4x8 в зависимости от установленной длины блока (допускается использование нескольких фиксированных размеров шифруемого блока информации). Далее на соответствующих этапах производятся преобразования либо над независимыми столбцами, либо над независимыми строками, либо вообще над отдельными байтами. Алгоритм AES состоит из определенного количества раундов (от 10 до 14 - это зависит от размера блока и длины ключа) и выполняет четыре преобразования: BS (ByteSub) - табличная замена каждого байта массива; SR (ShiftRow) - сдвиг строк массива. При этой операции первая строка остается без изменений, а остальные циклически побайтно сдвигаются влево на фиксированное число байтов, зависящее от размера массива. Например, для массива размером 4x4 строки 2, 3 и 4 сдвигаются соответственно на 1, 2 и 3 байта; МС (MixColumn) - операция над независимыми столбцами массива (рис. 2.11), когда каждый столбец по определенному правилу умножается на фиксированную матрицу с(х); АК (AddRoundKey) - добавление ключа. Каждый бит массива складывается по модулю 2 с соответствующим битом ключа раунда, который, в свою очередь, определенным образом вычисляется из ключа шифрования. Эти преобразования воздействуют на массив state, который адресуется с помощью указателя 'state'. Преобразование AddRoundKey использует дополнительный указатель для адресации ключа раунда Round Key. Преобразование BS (ByteSub) является нелинейной байтовой подстановкой, которая воздействует независимо на каждый байт массива state, используя таблицу замен (подстановок) S-box. В каждом раунде (с некоторыми исключениями) над шифруемыми данными поочередно выполняются перечисленные преобразования. Исключения касаются первого и последнего раундов: перед первым раундом дополнительно выполняется операция АК, а в последнем раунде отсутствует МС. Количество раундов шифрования R в алгоритме AES переменное (10, 12 или 14 раундов) и зависит от размеров блока и ключа шифрования (для ключа также предусмотрено несколько фиксированных размеров). Все преобразования в шифре AES имеют строгое математическое обоснование. Сама структура и последовательность операций позволяют выполнять данный алгоритм эффективно как на 8-битовых так и на 32-битовых процессорах. В структуре алгоритма заложена возможность параллельного исполнения некоторых операций, что может поднять скорость шифрования на многопроцессорных рабочих станциях в четыре раза. Вопрос 2. Алгоритм шифрования данных, определяемый ГОСТ 28147-89. Этот алгоритм криптографического преобразования данных предназначен для аппаратной и программной реализации, удовлетворяет криптографическим требованиям и не накладывает ограничений на степень секретности защищаемой информации. Алгоритм шифрования данных, определяемый ГОСТ 28147-89, представляет собой 64-битовый блочный алгоритм с 256-битовым ключом. 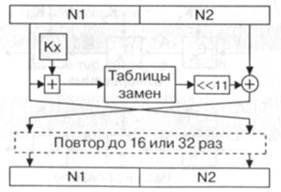 Рис. 11. Схема алгоритма ГОСТ 28147-89 Данные, подлежащие зашифрованию, разбивают на 64-разрядные блоки. Эти блоки разбиваются на два субблока N1 и N2 по 32 бит (рис. 11.). Субблок N1 обрабатывается определенным образом, после чего его значение складывается со значением субблока N2 (сложение выполняется по модулю 2, то есть применяется логическая операция XOR - исключающее ИЛИ), а затем субблоки меняются местами. Данное преобразование выполняется определенное число раз (раундов): 16 или 32 в зависимости от режима работы алгоритма. В каждом раунде выполняются следующие операции. Первая операция - наложение ключа. Содержимое субблока N1 складывается по модулю 232 с 32-битовой частью ключа Кх. Полный ключ шифрования представляется в виде конкатенации 32-битовых подключей: КО, K1, К2, КЗ, К4, К5, К6, К7. В процессе шифрования используется один из этих подключей - в зависимости от номера раунда и режима работы алгоритма. Вторая операция - табличная замена. После наложения ключа субблок N1 разбивается на 8 частей по 4 бита, значение каждой из которых заменяется в соответствии с таблицей замены для данной части субблока. Затем выполняется побитовый циклический сдвиг субблока влево на 11 бит. Табличные замены. Блок подстановки S-box (Substitution box) часто используются в современных алгоритмах шифрования, поэтому стоит пояснить, как организуется подобная операция. Блок подстановки S-box состоит из восьми узлов замены (5-блоков замены) S1, S2,S8 с памятью 64 бит каждый. Поступающий на блок подстановки S 32-битовый вектор разбивают на восемь последовательно идущих 4-битовых векторов, каждый из которых преобразуется в 4-битовый вектор соответствующим узлом замены. Каждый узел замены можно представить в виде таблицы-перестановки шестнадцати 4-битовых двоичных чисел в диапазоне 0000 - 1111. Входной вектор указывает адрес строки в таблице, а число в этой строке является выходным вектором. Затем 4-битовые выходные векторы последовательно объединяют в 32-битовый вектор. Узлы замены (таблицы-перестановки) представляют собой ключевые элементы, которые являются общими для сети ЭВМ и редко изменяются. Эти узлы замены должны сохраняться в секрете. Алгоритм, определяемый ГОСТ 28147-89, предусматривает четыре режима работы: простой замены, гаммирования, гаммирования с обратной связью и генерации имитоприставок. В них используется одно и то же описанное выше шифрующее преобразование, но, поскольку назначение режимов различно, осуществляется это преобразование в каждом из них по-разному. В режиме простой замены для зашифрования каждого 64-битового блока информации выполняются 32 описанных выше раунда. При этом 32-битовые подключи используются в следующей последовательности: КО, K1, К2, КЗ, К4, К5, Кб, К7, КО, K1 и т.д. - в раундах с 1-го по 24-й; К7, К6, К5, К4, КЗ, К2, K1, КО - в раундах с 25-го по 32-й; Расшифрование в данном режиме проводится точно так же, но с несколько другой последовательностью применения подключей; КО, K1, К2, КЗ, К4, К5, К6, К7 - в раундах с 1-го по 8-й; К7, К6, К5, К4, КЗ, К2, K1, КО, К7, К6 и т.д. - в раундах с 9-го по 32-й. Все блоки шифруются независимо друг от друга, то есть результат зашифрования каждого блока зависит только от его содержимого (соответствующего блока исходного текста). При наличии нескольких одинаковых блоков исходного (открытого) текста соответствующие им блоки шифртекста тоже будут одинаковы, что дает дополнительную полезную информацию для пытающегося вскрыть шифр криптоаналитика. Поэтому данный режим применяется в основном для шифрования самих ключей шифрования (очень часто реализуются многоключевые схемы, в которых по ряду соображений ключи шифруются друг на друге). Для шифрования собственно информации предназначены два других режима работы - гаммиования и гаммирования с обратной связью. В режиме гаммирования каждый блок открытого текста побитно складывается по модулю 2 с блоком гаммы шифра размером 64 бит. Гамма шифра - это специальная последовательность, которая получается в результате определенных операций с регистрами N1 и N2: 1. В регистры N1 и N2 записывается их начальное заполнение - 64-битовая величина, называемая синхропосылкой. 2. Выполняется зашифрование содержимого регистров N1 и N2 (в данном случае синхропосылки) в режиме простой замены. 3. Содержимое регистра N1 складывается по модулю (232 - 1) с константой С1 - 224 + 216 + 28 + 24, а результат сложения записывается в регистр N1. 4. Содержимое регистра N2 складывается по модулю 232 с константой С2 = 224 + 216 + 28 + 1, а результат сложения записывается в регистр N2. 5. Содержимое регистров N1 и N2 подается на выход в качестве 64-битового блока гаммы шифра (в данном случае N1 и N2 образуют первый блок гаммы). 6. Если необходим следующий блок гаммы (то есть необходимо продолжить зашифрование или расшифрование), выполняется возврат к операции 2. Для расшифрования гамма вырабатывается аналогичным образом, а затем к битам зашифрованного текста и гаммы снова применяется операция ХOR. Поскольку эта операция обратима, в случае правильно выработанной гаммы получается исходный текст Для выработки нужной для расшифровки гаммы шифра у пользователя, расшифровывающего криптограмму, должен быть тот же ключ и то же значение синхропосылки, которые применялись при зашифровании информации. В противном случае получить исходный текст из зашифрованного не удастся. В большинстве реализаций алгоритма ГОСТ 28147-89 синхропосылка не секретна, однако есть системы, где синхропосылка - такой же секретный элемент, как и ключ шифрования. Для таких систем эффективная длина ключа алгоритма (256 бит) увеличивается еще на 64 бит секретной синхропосылки, которую также можно рассматривать как ключевой элемент. Рассматривая режим генерации имитоприставок, следует определить понятие предмета генерации. Имитоприставка - это криптографическая контрольная сумма, вычисляемая с использованием ключа шифрования и предназначенная для проверки целостности сообщений. При генерации имитоприставки выполняются следующие операции: первый 64-битовый блок массива информации, для которого вычисляется имитоприставка, записывается в регистры N и N2 зашифровывается в сокращенном режиме простой замены (выполняются первые 16 раундов из 32). Полученный результат суммируется по модулю 2 со следующим блоком информации с сохранением результата в N1 и N2. Цикл повторяется до последнего блока информации. Получившееся в результате этих преобразований 64-битовое содержимое регистров N1 и N2 или его часть и называется имитоприставкой. Размер имитоприставки выбирается исходя из требуемой достоверности сообщений: при длине имитоприставки r бит вероятность, что изменение сообщения останется незамеченным, равна 2-r. Чаще всего используется 32-битовая имитоприставка, то есть половина содержимого регистров. Этого достаточно, поскольку, как любая контрольная сумма, имитоприставка предназначена, прежде всего, для защиты от случайных искажений информации. Для защиты же от преднамеренной модификации данных применяются другие криптографические методы - в первую очередь электронная цифровая подпись. При обмене информацией имитоприставка служит своего рода дополнительным средством контроля. Она вычисляется для открытого текста при зашифровании какой-либо информации и посылается вместе с шифртекстом. После расшифрования вычисляется новое значение имитоприставки, которое сравнивается с присланной. Если значения не совпадают - значит, шифртекст был искажен при передаче или при расшифровании использовались неверные ключи. Особенно полезна имитоприставка для проверки правильности расшифрования ключевой информации при использовании многоключевых схем. Алгоритм ГОСТ 28147-89 считается очень стойким - в настоящее время для его раскрытия не предложено более эффективных методов, чем упомянутый выше метод «грубой силы». Его высокая стойкость достигается в первую очередь за счет большой длины ключа - 256 бит. При использовании секретной синхропосылки эффективная длина ключа увеличивается до 320 бит, а засекречивание таблицы замен прибавляет дополнительные биты. Кроме того, криптостойкость зависит от количества раундов преобразований, которых по ГОСТ 28147-89 должно быть 32 (полный эффект рассеивания входных данных достигается уже после 8 раундов). Вопрос 3. Достоинства и недостатки симметричных систем шифрования. Алгоритмы симметричного шифрования используют ключи относительно небольшой длины и могут быстро шифровать большие объемы данных. При симметричной методологии шифрования отправитель и получатель применяют для осуществления процессов шифрования и расшифрования сообщения один и тот же секретный ключ. Алгоритмы симметричного шифрования строятся исходя из предположения, что зашифрованные данные не сможет прочитать никто из тех, кто не обладает ключом для их расшифрования. Если ключ не был скомпрометирован, то при расшифровании автоматически выполняется аутентификация отправителя, так как только отправитель имеет ключ, с помощью которого можно зашифровать информацию, и только получатель имеет ключ, позволяющий расшифровать информацию. Алгоритмы симметричного шифрования применяются для абонентского шифрования данных - то есть для шифрования информации, предназначенной для отправки кому-либо, например, через Интернет. Использование только одного секретного ключа для всех абонентов сети, конечно, недопустимо по соображениям безопасности: в случае компрометации (утери, хищения) ключа под угрозой будет находиться документооборот всех абонентов сети. Порядок использования систем с симметричными ключами: 1. Симметричный секретный ключ должен создаваться, распространяться и сохраняться безопасным образом. 2. Для получения зашифрованного текста отправитель применяет к исходному сообщению симметричный алгоритм шифрования вместе с секретным симметричным ключом. Таким образом, неявно подготавливается аутентификация отправителя и получателя, так как только отправитель знает симметричный секретный ключ и может зашифровать этот текст. Только получатель знает симметричный секретный ключ и может расшифровать этот текст. 3. Отправитель передает зашифрованный текст. Симметричный секретный ключ никогда не передается в открытой форме по незащищенным каналам связи. 4. Получатель применяет к зашифрованному тексту тот же самый симметричный алгоритм шифрования/расшифрования вместе с тем же самым симметричным ключом (который уже есть у получателя) для восстановления исходного текста. Его успешное восстановление аутентифицирует того, кто знает секретный ключ. Для симметричных криптосистем актуальна проблема безопасного распределения симметричных секретных ключей. Всем системам симметричного шифрования присущи следующие недостатки: принципиальным является требование защищенности и надежности канала передачи секретного ключа для каждой пары участников информационного обмена; предъявляются повышенные требования к службе генерации и распределения ключей, обусловленные тем, что для N абонентов при схеме взаимодействия «каждый с каждым» требуется Nх(N- 1) / 2 ключей, то есть зависимость числа ключей от числа абонентов является квадратичной; например, для п = 1000 абонентов требуемое количество ключей будет равно 1000х(1000-1)/2 = 499 500 ключей. Поэтому без эффективной организации защищенного распределения ключей широкое использование обычной системы симметричного шифрования в больших сетях и, в частности, в глобальных сетях практически невозможно. Перечень литературы и Интернет-ресурсов: 1. А.П. Алферов, А.Ю. Зубов, А.С. Кузьмин, А.В. Черемушкин. Основы криптографии: Учебное пособие. – М.: Гелиос АРВ, 2005. стр. 52-59. 2. В.М. Фомичев. Дискретная математика и криптология Курс лекций. – М.: ДИАЛОГ-МИФИ, 2003. стр. 135-143. 3. Шаньгин В.Ф. Защита компьютерной информации. Эффективные методы и средства. – М.: ДМК Пресс, 2008. стр. 147-154. 4. http://www.fstec.ru/ 5. http://www.cryptopro.ru/ |
