Методы проекции. 1 Методы проекции и метод преобразования ортогональной проекции 1 Описание и основные методы преобразования проекций
 Скачать 219.47 Kb. Скачать 219.47 Kb.
|
|
1 Методы проекции и метод преобразования ортогональной проекции 1.1 Описание и основные методы преобразования проекций Количество графических структур, необходимых для решения задач, во многом зависит не только от сложности задачи, но и от расположения пространственной формы в проекте относительно плоскости проекции. Графическое изображение должно удовлетворять требованиям, относящимся к позиционным и метрическим расчетам. Приемлемым для решения подобных задач является создание новой дополнительной проекции из результатов двух заданных проекций. Дополнительные проекции отдельных элементов, либо эти проекции позволяет получать элементы в точном размере. Создание дополнительных проекций – это преобразование чертежа. Преобразование также может быть выполнено следующими способами: - способ замещения плоскостей проекций при условии, что рассматриваемый объект или его элементы занимают одно из отдельных мест относительно новой плоскости проекций; - способ повернуть геометрический образ таким образом, чтобы он занимал отдельное место относительно плоскости проекции в соответствии с заданным условием задачи; - замена направления проекций в системе известных плоскостей проекций или путем введения новой плоскости проекций 1.2 Способы замены плоскости проекции Ортогональная схема, представленная при решении графических задач, в большинстве случаев не может дать наглядного представления о предмете и его отдельных элементах, не может быть легкой при решении позиционных и метрических задач. Иногда приходится создавать дополнительные схемы, которые могут быть решением данной задачи или результатом ее упрощения. Такие дополнительные чертежи можно построить методом замещения плоскостей проекций. Но предмет сохраняет осевое положение в пространстве. Меняет направление плоскостей проекций: при замещении обязательно соблюдается взаимная перпендикулярность двух плоскостей проекций. На рисунке 1 приведено изображение плоскостей проекций в пространстве и точка А с ортогональными проекциями А1 и А2 в плоскости П1 и П2. Дополнительная вертикальная плоскость П4 с горизонтальной плоскостью П1, перпендикулярная плоскость П1 образуют дополнительную систему плоскостей проекций. Аналогично показано построение дополнительной проекции А4 точки А на плоскости П4. Плоскость проекции П1 является общей для обеих систем основной П2 / П1 и дополнительной П4 / П1. 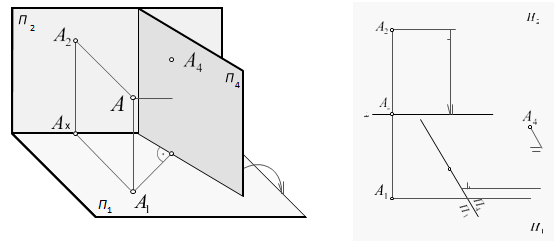 Рисунок 1. Изображение плоскостей проекций Расстояние между точкой А и плоскостью П1 одинаково как в первой, так и во второй системах, т. е. аппликатура ZA и горизонтальная проекция точки А2 на А1 остаются неизменными для обеих систем. Переход от одной системы плоскости проекции к другой можно легко проследить даже по ортогональной схеме (рисунок 2). Точка А представлена проекциями А1 и А2 в системе плоскостей проекций П2 / П1. Проекционная ось дополнительно построенной проекционной плоскости П4 определяет на чертеже дополнительную систему плоскостей проекций П2 / П1. Плоскость А4 точки А на плоскости П1 прямая (проекционная линии связи), расположенных на расстоянии za от перпендикулярной оси на расстоянии от нее от точки А до горизонтальной плоскости проекции П1. Объем ZA будет известен по основному чертежу.  Рисунок 2. Ортогональная схема На рисунках 2, 3 дополнительную систему плоскостей проекций определяют две взаимно перпендикулярные плоскости П2 и П4. Замена одной плоскости проекции в большинстве случаев не может дать окончательного решения данной задачи. Иногда вам придется заменить две или более плоскостей проекции. Дополнительные плоскости проекций выбираются из условий задачи, изменяющей плоскости проекций. Если дополнительная плоскость проекции параллельна прямому отрезку или плоской фигуре, то такой отрезок проецируется на эту плоскость проекции без изменения ее первоначального объема.  Рисунок 3. Взаимно перпендикулярные плоскости П2 и П4 Определим реальный объем плоской фигуры проектируемой плоскости, заданной в состоянии треугольника (рисунок 4). Предположим, что треугольник АВС лежит в плоскости, проецируемой Q. Выбираем дополнительную плоскость проекции П3 параллельно плоскости треугольника и определяем дополнительные проекции высот А4, В4 и С4 треугольника А, В и С. Проекция А4В4С4 показывает начальный объем треугольника АВС. Проекция М4 точки М произвольно выбрана на плоскости треугольника. На рисунке 4 приведено построение основных проекций М1 и М2 этой точки. Если плоская фигура расположена самостоятельно (в целом) относительно основных координатных плоскостей проекции, то ее объем определяется с помощью замены двух последующих плоскостей проекций. В дополнение к основному чертежу создается еще два чертежа плоских фигур. С помощью первого дополнительного чертежа можно представить фигуру, лежащую в проектируемой плоскости; второй дополнительный чертеж дает представление о фигуре, лежащей в плоскости, параллельной плоскости проекции и определяющей ее реальный объем. При перестановке свободно расположенной плоскости в проектируемую плоскость необходимо выбрать одну из главных линий в этой плоскости – горизонтальную или фронтальную, каждая из которых определяет направление дополнительных плоскостей проекции. При замене плоскости в произвольном положении на проектируемую плоскость П1 и П2 определяют углы α и наклон β заданной плоскости плоскостей проекций.  Рисунок 4. Плоскость, заданная в состоянии треугольника Если треугольник горизонтальный-это направление дополнительной плоскости проекции, то треугольник перпендикулярен этой плоскости проекции, т. е. занимает место проецируемой плоскости. При этом определяется угол α проекционной наклонной плоскости П1. Если фронт треугольника является направлением дополнительной плоскости проекции, то треугольник перпендикулярен этой плоскости проекции и имеет место относительно проектируемой плоскости. При этом определяется угол β проекционной фронтальной плоскости П2. Плоская фигура в произвольном положении изображается в виде проецирования относительно дополнительной плоскости проекции. Рассмотрим строение, пусть часть произвольно расположенной плоскости задана в виде треугольника АВС (рисунок 5). Фронтальная через высоту А. А2В2 фронта указывает направление проецирования фронта в сторону дополнительной плоскости фронта. Выбираем проекцию П4 перпендикулярно фронту Af. В направлении проекции точки С (связь линии) обозначим его дополнительную проекцию С4 и проведем основную линию расчета перпендикулярно линии связи. Обозначим разность координат ув-ус точек В и С и определим дополнительную проекцию В4 точки В. Аналогично, А и ???? обозначим разность координат уа-ус точек и определим дополнительную проекцию А4 точки А. Проекции А4, В4, С4 точек А, В и С определяют положение следа плоскости треугольника, расположенного на одной прямой и являющегося проецирующим относительно дополнительной плоскости проекции П3. Направление наклона этой плоскости к основной линии разности угла α является углом наклона плоскости треугольника относительно фронтальной плоскости проекции П2.  Рисунок 5. Плоскость, заданная в виде треугольника АВС Покажем графическую структуру для определения действительного размера треугольника АВС в произвольном положении (рисунок 6). Задача решается путем подстановки двукратных плоскостей проекций. Проецируем фронтальную плоскость проекции П2 на дополнительно проецируемую плоскость проекции П4. Если направление плоскости П4 горизонтально плоской фигуре, то фигура вновь вставляется в проецируемую плоскость. Треугольник, проходящий через высоту В, определяет направление дополнительной плоскости проекции горизонтали П4. На плоскости П4 получаем падающую проекцию горизонтали и треугольника. Проецируется на горизонтальную точку, а треугольник проецируется на отрезок прямой. Подставив горизонтальную плоскость проекции П1 в параллельную плоскость фигуры – дополнительную плоскость П4, получим точное объемное изображение фигуры в плоскости П4.  Рисунок 6. Треугольника АВС в произвольном положении 1.3 Способы поворота Этот метод предусматривает построение дополнительных чертежей предмета в неизменной основной системе плоскостей проекций путем поворота этого предмета вокруг оси. Применяется при изучении различных вращающихся форм конструкций механизмов и машин. Вращение вокруг проектируемых прямых Вращая предмет, можно построить множество рисунков этого предмета в одной основной системе плоскостей проекций. Но плоскости проекций остаются неизменными. Рассматриваемое вещество приводит к новому состоянию путем поворота вокруг осей, перпендикулярных плоскостям проекций. В новом случае строится его ортогональная проекция, т. е. схема предмета. Рассмотрим поворот точки вокруг осей, перпендикулярных плоскости проекции. Предположим, что точка А (рисунок 7) вращается вокруг горизонтально проецируемой прямой i. Траектория движения точки А представляет собой центральную окружность О на оси поворота. Плоскость Ф окружности - горизонтальная и перпендикулярная оси поворота. Мы называем это плоскостью копирования (перемещения) точки. Радиус А1О1 проецируется в горизонтальной плоскости проекции. Вращая вокруг осей, можно определить совместные проекции точки А. Горизонтальная проекция А1 по дуге окружности, а фронтальная А2 по горизонтальной прямой – по следу Фп2 заменяется плоскостью замещения точки А. 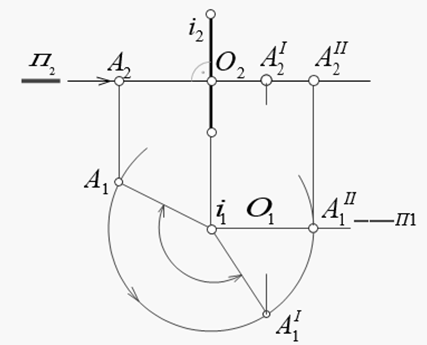 Рисунок 7. Поворот точки вокруг осей, перпендикулярных плоскости проекции Точка А1 определяется поворотом точки А вокруг осей на угол α в направлении, обратном направлению часовой стрелки. Вращая точку А2 вокруг оси прямой I, она сливается с фронтальной плоскостью г. Плоская параллельная замена. Для переосмысления ортогональной схемы геометрической фигуры эту фигуру можно сделать и плоскопараллельной заменой, т. е. все ее точки находятся на плоскостях, переносятся на параллельные плоскости проекции. При этом проекция фигуры не изменяется ни по объему, ни по типу в любом случае плоскости проекции. Он меняет только свое положение относительно оси проекции. Проекции траекторий точек на другую плоскость проекции представляют собой след движения плоскостей этих точек, т. е. ось проекции в направлении прямой, параллельной. Плоскопараллельную замену можно заменить поворотом без указания осей, т. е. поворотом вокруг проектируемой прямой без деления [4]. Вращение проекции вокруг прямых, параллельных плоскостей. В проекции истинной величины плоской фигуры этот уровень равен прямому - можно определить вращением прямой фигуры вокруг параллельной плоскости проекции. В этом случае плоское геометрическое изображение может быть приведено в положение, параллельное плоскости проекции, вращаясь один раз вокруг оси. 1.4 Особенности и свойства ортогональной проекции Все свойства параллельного и центрального проецирования свойственны ортогональному проецированию, и обосновывается теорема прямоугольного проецирования: если хотя бы одна сторона прямого угла параллельна плоскости проекции, а другая не перпендикулярна ей, то прямой угол в этой плоскости проецируется как прямой угол. При выполнении чертежей используется ортогональное проецирование методом бусинки - ортогональное проецирование на две взаимно перпендикулярные проекционные плоскости: П1-горизонтальную и П2-фронтальную. Проекция оси называется плоскостью Р1 на пересекающуюся плоскость и прямую Р2. Для создания чертежа плоскости Р1 ее совмещают с плоскостью Р2, вращая ее вокруг оси О. Создаваемое таким образом изображение часто называют диаграммой Монжа. Плоскости проекций делят пространство на прямоугольные четверти. При выполнении ортогональных проекций предполагается, что наблюдатель будет находиться на бесконечном расстоянии от плоскостей проекций в первой четверти. Графическая модель объекта любой сложности рассматривается как геометрическое положение точек, взаимное расположение которых может дать представление о форме объекта. Положение объекта в пространстве оценивается по расположению точек относительно системы координат. Таким образом, рассматривая процесс проектирования точки в плоскостях Р1 и Р2, можно создать алгоритм рисования объекта. При проецировании точка принимается за физический объект. Частный случай параллельного проецирования, когда ортогональное (прямоугольное) направление проецирования-проецирования перпендикулярно плоскости проецирования. В этом случае проекция геометрических фигур называется ортогональной. Ортогональная проекция характеризуется всеми свойствами параллельной проекции, а также свойствами, уникальными для ортогональной проекции. Первое свойство. В общем случае ортогональная проекция отрезка всегда меньше его естественной длины. Если вы * B || Если нарисовать А1В1, то РАА * в = 90°. Из прямоугольного треугольника AB — гипотенуза, Al*b — катет, причем гипотенуза всегда больше катета (a*B = AB Soca), Рассмотрим частные случаи: Если А = 0 Þ |А1В1 | = |AB/, т. е. проекция равна самому отрезку. Если а = 90°С А1 = В1, т.е. проекция отрезка является точкой. Второе свойство: теорема о проекции прямого угла Если одна сторона прямого угла параллельна плоскости некоторой проекции, а другая сторона перпендикулярна ей, то плоскость проекции не меняется на рабочие прямоугольника. Дано: РАВС = 90°, вс // Р1, Доказательство: плоскость Ф = а в СВ 1 плоскость s = AK Ç BB1 Как ^ F, т. е. к. как ^ AB и As ^ BB1, но A1C1 || как Þ В1С1 ^ Ә1С1 ^ А1В1, следовательно, Р1В1С1 является прямым/ Третье свойство: ортогональная проекция окружности обычно является эллипсом. Окружность в плоскости s, SU P1 = a, если 0 AB ^ CD-объединенные диаметры, AB || Пусть P1 A1v1 = AB — большая ось эллипса. С1d1 = СD – малая ось эллипса. Все хорды окружности, параллельные CD, проецируются коэффициентом сжатия и делятся пополам осью a1v1, т.е. ортогональная проекция окружности, вообще говоря, имеет замкнутую центральную симметричную кривую второго порядка с двумя взаимно перпендикулярными оси. Исключения: 1. Если S//P1, то круг (k) проецируется без искажений. 2. Если S ^ P1, т. е. Ða = 90°, то окружность (k) представляет собой прямую, равную диаметру. |
