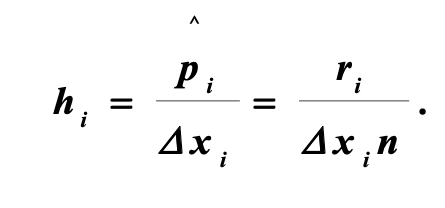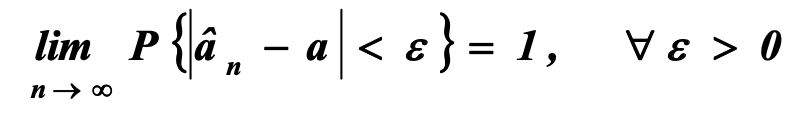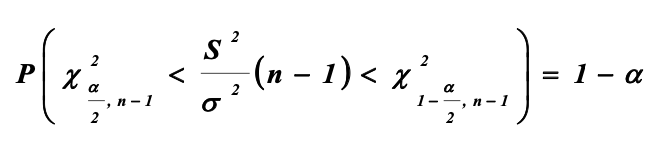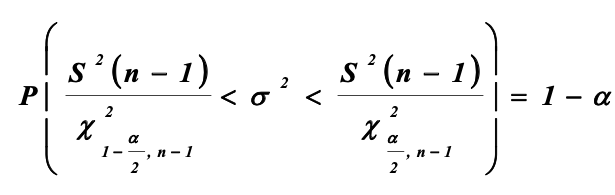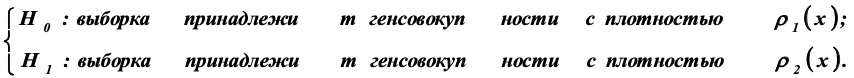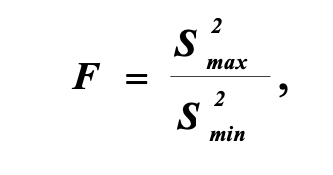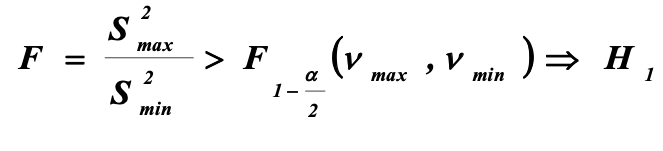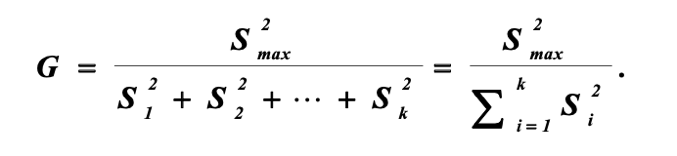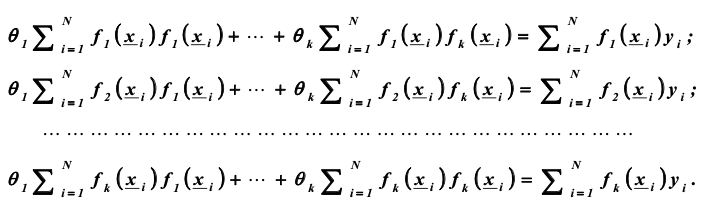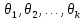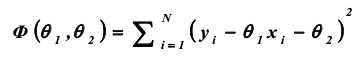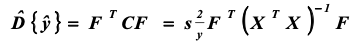|
вопросы. ВОПРОСЫ К ЗАЧЕТУ. 1. Модель это материальный или воображаемый объект, который в процессе познания замещает реальный объект, сохраняя при этом его существенные свойства. (Любой образ объекта, любое представление об объекте). Виды моделей
ВОПРОСЫ К ЗАЧЕТУ.
1.Модель – это материальный или воображаемый объект, который в процессе познания замещает реальный объект, сохраняя при этом его существенные свойства. (Любой образ объекта, любое представление об объекте).
Виды моделей:
Математические модели принято разделять на статические и динамические.
Статические модели описывают связь между входными и выходными параметрами объекта в стационарном состоянии, т.е. при условии, что ни входные, ни выходные параметры не изменяются во времени. Реально это соответствует ситуации, когда на вход объекта подается постоянное, не изменяющееся во времени воздействие, а значение выходного параметра фиксируется лишь после того, как его величина установится, т.е. перестанет изменяться во времени. С математической точки зрения статическая модель представляет собой функцию, т.е. математический объект, который одному или нескольким числам (значениям входных параметров) ставит в соответствие число (или несколько чисел), равное величине выходного параметра (параметров).
Динамические модели связывают вход и выход объекта в переходных состояниях, т.е. учитывают такие, присущие каждому реальному объекту, свойства, как инерционность, способность «помнить» свои предыдущие состояния и т.д. Математически динамическая модель представляет собой оператор, т.е. математический объект, который одной или нескольким функциям времени, задающим изменение во времени входных пара- метров, ставит в соответствие функцию (или несколько функций) времени, задающих изменение во времени выходного параметра (параметров). Конкретные математические структуры, реализующие оператор, могут быть различны. Наиболее часто используются дифференциальные уравнения, передаточные функции, корреляционные и спектральные зависимости и т.д.
Математическая модель – модель, представленная с помощью математических формул. Математическая модель является корректной, если для неё осуществлён и получен положительный результат всех контрольных проверок: размерности, порядков, характера зависимостей, экстремальных ситуаций, граничных условий, физического смысла и математической замкнутости.
Характеристики численных методов:
Численные методы позволяют находить экстремумы для любых уравнений с заданной точностью, они не требуют вычисления производных и позволяют находить экстремумы, которые локализованы в определённом интервале, но они требуют большого объёма вычислений. Развитие вычислительной техники позволило в настоящее время широко использовать последние методы.
Устойчивость метода. Неустойчивый метод приводит к накоплению погрешности вычислений. Признак неустойчивости – решение имеет пилообразный вид, амплитуда достигает предельных порядков.
Порядок метода. Любой численный метод имеет порядок точности, который характеризует погрешность метода.
2. Вероятность и ее свойства:
Вероятностью события А в данной массовой операции называется отношение среднего числа единичных операций n, в которых событие А происходит, к объему массовой операции m:
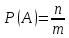
Свойства:
- вероятность может принимать значения в пределах только от нуля до единицы:
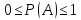
- если событие невозможно, то его вероятность равна нулю, а если событие достоверно, то его вероятность равна единице. (Обратные утверждения неверны, т.е. если вероятность события равна нулю, то оно не обязательно невозможно, а если вероятность равна единице, то событие не обязательно достоверно.)
Теорема сложения:
Вероятность появления одного из двух несовместимых событий, равна сумме вероятностей этих событий:
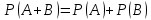
Следствие. Сумма вероятностей противоположных событий равна 1
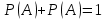
2. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления.
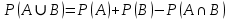
Полная группа событий:
Если n событий Аi взаимно несовместны и, кроме того, они вместе исчерпывают все возможные исходы эксперимента, то они составляют полную группу событий. Так как в ходе эксперимента какое-нибудь из этих событий достоверно произойдет, то, очевидно, что в этом случае
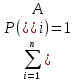
(например – игральная кость. Выпадение любой из граней достоверно означает не выпадение всех остальных (несовместность), а так как какая-нибудь грань выпадет обязательно, то включение всех шести граней в полную группу событий обеспечивает исчерпание всех возможных исходов опыта.)
Условная вероятность:
Условной вероятностью называется вероятность события B, вычисленная в предположении, что событие А уже наступило.

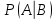 и и 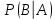 – условные вероятности – условные вероятности
Формула Байеса:
Суть формулы Байеса определяется следующей теоремой.
Теорема Байеса. Пусть события А1, А2,...,Аn составляют полную группу. Пусть также имеется некоторое событие В, имеющее ненулевую вероятность. Тогда
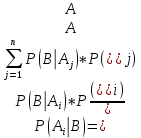
Схема и формула Бернулли:
Схемой Бернулли называется система из n независимых испытаний, в каждом из которых могут иметь место «успех» или «неудача» с постоянными вероятностями. Другими словами, схема Бернулли представляет со- бой n-кратное повторение опыта, который может иметь только два исхода, и при этом вероятности каждого из исходов не меняются от опыта к опыту. Для удобства один из исходов обозначается как «успех», а другой – как «неудача».
Формула Бернулли.
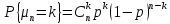 , ,
Где p – вероятность «успеха» в единичном испытании, а 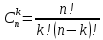 – биноминальный коэффициент или, что то же самое, число сочетаний из n по k. – биноминальный коэффициент или, что то же самое, число сочетаний из n по k.
Теорема умножения вероятностей:
Вероятность произведения двух событий и (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило:
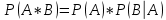
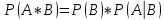
Следствие. Вероятность произведения двух независимых событий и равно произведению вероятностей этих событий.
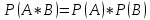
Формула полной вероятности:
Формула полной вероятности является очень важным инструментом для вычисления вероятностей сложных событий.
Пусть события А1, А2, ..., Аn составляют полную группу. Тогда, если известны условные вероятности осуществления произвольного события В при условии осуществления каждого из событий, составляющих полную группу, можно найти безусловную вероятность осуществления события В:
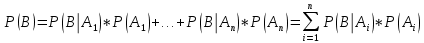
3. Случайные величины и их описание:
Во множестве недетерминированных величин можно выделить подмножество таких величин, обладающих статистической устойчивостью, значение которых можно предсказать в среднем. Такие величины называются случайными.
Величина, значение которой не может быть предсказано в точности до тех пор, пока не произведен эксперимент, называется недетерминированной.
Биномиальная случайная величина μn. Представляет собой число успехов в схеме Бернулли из n испытаний с постоянной вероятностью успеха в каждом испытании, равном р. Множество Х ее значений конечно и состоит из n+1 элементов:
X 0,1,2,,n.
Пуассоновская случайная величина. Представляет собой предельный случай биномиальной случайной величины при n и p 0 .
Множество значений пуассоновской случайной величины бесконечно (счётно):
X 0,1,2,,
Равномерная случайная величина. Представляет собой непрерывную случайную величину, равномерно распределенную на некотором интервале a, b. Она не может принимать значений вне этого интервала, а внутри интервала все значения равновероятны. Поэтому функция плотности распределения равномерной случайной величины имеет вид:
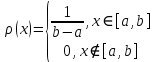
Нормальная (гауссовская) случайная величина. Эта случайная величина определена на всей числовой оси – от минус бесконечности до плюс бесконечности. Функция плотности ее распределения имеет вид:
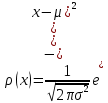
Функции распределения и плотности:
Исчерпывающим описанием любой случайной величины является функция распределения.
Свойства функции распределения:
1. Так как функция распределения представляет собой вероятность, то она изменяется от нуля до единицы: 0 F x 1 .
2. Функция распределения является неубывающей функцией, т.е. из того, что x2>x1, следует, что F x2 F x1 ,что в математической записи выглядит как x2 x1 Fx2Fx1.
3. Вероятность того, что случайная величина находится в интервале от x1 до x2, равна разности значений функции распределения от этих аргументов: Px1 x2Fx2Fx1.
4. Значение функции распределения в минус бесконечности равно нулю: F 0.
5. Значение функции распределения в плюс бесконечности равно единице: F 1.
Функция плотности распределения, которая представляет собой производную от функции распределения:
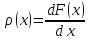
Свойства функции плотности распределения:
Функция плотности всегда неотрицательная 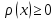 , что с учетом формулы выше следует из того, что функция распределения – неубывающая. , что с учетом формулы выше следует из того, что функция распределения – неубывающая.
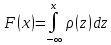
Вероятность того, что случайная величина находится в интервале от х1 до х2 равна: 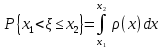 . .
Условие нормировки 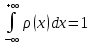
Дискретные и непрерывные СВ:
В зависимости от свойств множества значений случайные величины подразделяются на дискретные и непрерывные.
Дискретной называется такая случайная величина, множество значений которой либо конечно, либо счётно.
Непрерывной называется такая случайная величина, множество значений которой несчётно.
Числовые характеристики СВ:
Математическое ожидание представляет собой средневзвешенное значение случайной величины. Формулы для его расчета у дискретных и непрерывных случайных величин различны.
Если ξ – дискретная случайная величина, принимающая значения x1 , x2 , с вероятностями p1 , p2 , ,то её математическое ожидание равно:
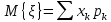
где суммирование производится по всем значениям, принимаемым случайной величиной.
Если ξ – непрерывная случайная величина с плотностью распределения ρ(x), то ее матожидание будет:
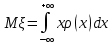
Дисперсией произвольной случайной величины ξ по определению является математическое ожидание квадрата отклонения этой случайной величины от своего матожидания, т.е.:
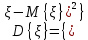
Моменты случайных величин
Начальным моментом r-го порядка случайной величины ξ называется математическое ожидание этой случайной величины в степени r:
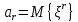
Асимметрия характеризует степень отклонения зеркальной симметрии относительно математического ожидания функции массы или функции плотности распределения. Она рассчитывается по формуле:
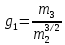
Эксцесс характеризует степень отклонения формы кривой плотности распределения от кривой плотности нормального распределения и рассчитывается по формуле:
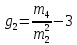
Нормальный закон распределения и центральная предельная теорема:
Если имеется большое число произвольно распределенных случайных величин, ни одна из которых не превосходит своим разбросом других, то сумма этих случайных величин распределена асимптотически по нормальному закону. (описан Гауссом, определяется теоремой Ляпунова).
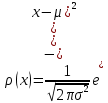
4. Многомерные СВ их описания:
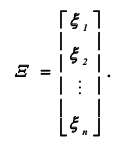
Совокупность из n случайных величин произвольной природы 1, 2, …, n, называется многомерной случайной величиной или, что то же самое, случайным вектором Ξ размерности n:
Основной характеристикой является многомерная функция распределения, которая определяется следующим образом:
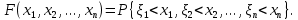
Если существует такая функция x1, x2, … , xn , которая при любых x1 , x2 , … , xn удовлетворяет равенству
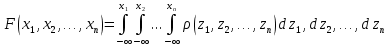
то эта функция называется функцией плотности распределения случайного вектора или многомерной функцией плотности распределения.
Числовые характеристики МСВ:
Математическое ожидание:
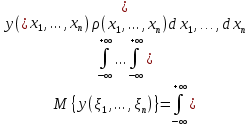
Моменты:
Моментом порядка r1 r2 rn случайного вектора Ξ относительно точки x1 ,x2 ,… ,xn называется величина
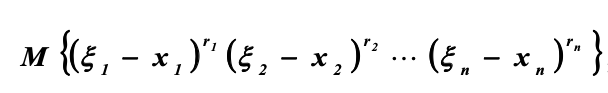
Ковариация:
В случае многомерных распределений особый интерес представляют центральные моменты второго порядка, которые называются ковариациями:
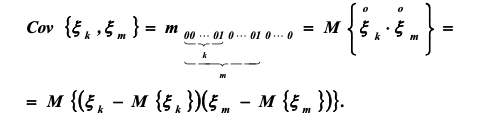
Дисперсная матрица:
Дисперсионную матрицу иногда называют ковариационной матрицей или матрицей дисперсий-ковариаций.
Дисперсионная матрица является квадратной матрицей размера [n×n] и представляет собой многомерный аналог дисперсии
Совокупность всех ковариаций определяет дисперсионную матрицу случайного вектора:
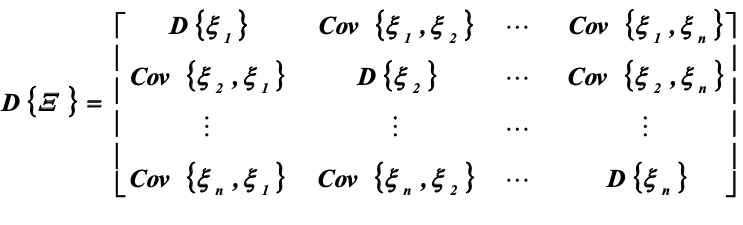
Генеральная совокупность:
Генеральная совокупность определяется как множество всех значений, которые может принимать некоторая случайная величина. Может быть конечной или бесконечной. Генеральная совокупность описывается некоторой неизвестной исследователю функцией распределения.
Выборка:
Выборкой размера n из генеральной совокупности, описываемой функции распределения F(x), называется набор n независимых случайных величин 1, 2, …, n, имеющих одну и ту же функцию распределения F(x).
Чтобы измерения n были выборкой, необходимо, чтобы они удовлетворяли двум условиям:
1) они должны быть независимыми, т.е. результаты одного эксперимента не должны каким-либо способом влиять на результаты остальных экспериментов;
2) все они должны описываться одним и тем же законом распределения, т.е. 1, 2, … , n F x .
Гистограмма:
Чтобы определить вид распределения определенной генеральной совокупности необходимо выдвинуть гипотезы о виде распределения. Для этого пользуются гистограммой, которая представляет собой состоятельную оценку функции плотности распределения.
Гистограмма строится следующим образом. Из выборки достаточно большого объема n выбираются наибольшее 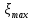 и наименьшее и наименьшее 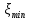 значения. Интервал [ значения. Интервал [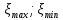 ] разбивается на k интервалов. Затем проводится подсчет количества попаданий ri случайных величин из выборки в каждый i интервал. ] разбивается на k интервалов. Затем проводится подсчет количества попаданий ri случайных величин из выборки в каждый i интервал.
Гистограмма строится следующим образом.
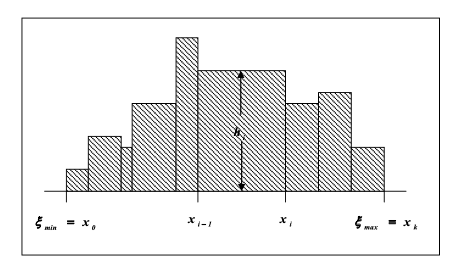
Над каждым из интервалов строится прямоугольник площадью:
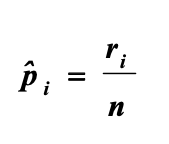
Одна сторона которого равна длине интервала 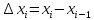 , а вторая (высота). , а вторая (высота).
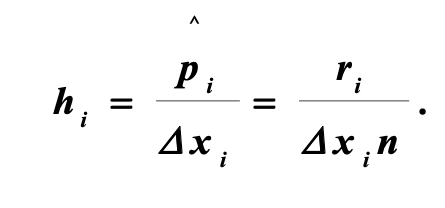
Точечные оценки и их характеристики:
Несмещенность:
Оценка называется несмещенной, если при любом объеме выборки математическое ожидание оценки равно оцениваемому параметру:
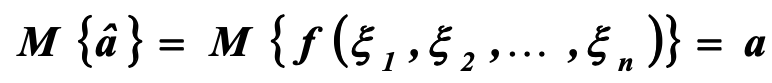
Состоятельность:
Оценка называется состоятельной, если равна единице вероятность того, что при неограниченном увеличении объема выборки n модуль разности между оценкой и оцениваемым параметром будет меньше сколь угодно малого положительного числа ε:
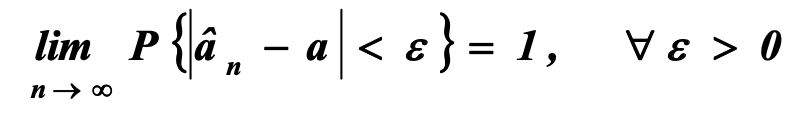
Эффективность:
При сравнении двух оценок одного и того же параметра более эффективной будет та, которая обладает меньшей дисперсией. Говорят так- же, что оценка является эффективной, если она имеет наименьшую дисперсию по сравнению со всеми возможными оценками данного параметра.
Доверительный интервал:
Это интервал, в котором с той или иной заранее заданной вероятностью находится генеральный параметр.
Определить доверительный интервал – это значит, во-первых, определить его границы, а во-вторых – указать доверительную вероятность, т.е. вероятность, с которой данный интервал содержит оцениваемый параметр.
Доверительный интервал для дисперсии:
Если указанная случайная величина подчиняется распределению Пирсона, то для нее можно записать:
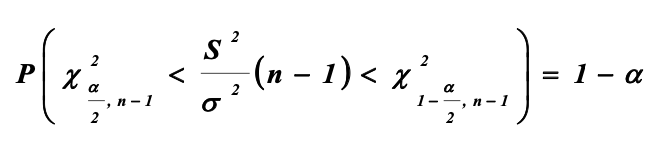
Преобразовав эту формулу, можно получить выражения для границ доверительного интервала дисперсии.
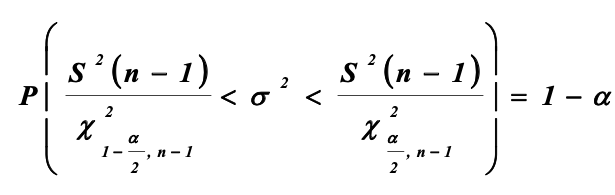
6.Проверка статистических гипотез:
Статистической гипотезой называется любое предположение о свойствах генеральной совокупности. статистические гипотезы бывают двух типов:
1) исходная или нулевая гипотеза (обозначается Н0);
2) конкурирующая или альтернативная гипотеза (обозначается Н1).
Решение задачи проверки статистических гипотез состоит в том, чтобы на основании анализа экспериментальных данных (т.е. выборки) отдать предпочтение одной из выдвинутых гипотез (Н0 или Н1).
Ошибка первого и второго рода:
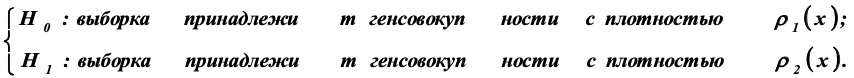
Можно отвергнуть гипотезу Н0, когда она на самом деле верна (такая ошибка называется ошибкой первого рода), и можно принять гипотезу Н0, когда она на самом деле неверна (ошибка второго рода).

Уровень значимости:
Вероятность ошибки первого рода α называется уровнем значимости и выбирается до начала эксперимента, исходя из различных эмпирических соображений, главным из которых является степень опасности по- следствий ошибки. В технике уровень значимости как правило равен 0,05, а в медицине часто бывает и 0,001.
Статистические критерии Фишера:
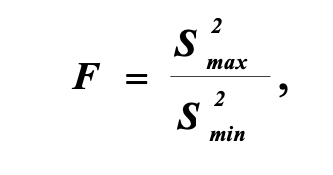
Значением критерия Фишера со степенями свободы max (число степеней свободы большей статистики) и min (число степеней свободы меньшей статистики). Гипотеза Н1 о статистически значимом различии дисперсий принимается тогда, когда значение решающей статистики больше табличного:
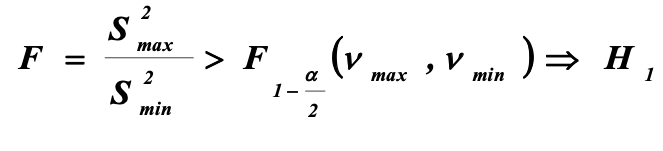
Стьюдента:

Кохрена:
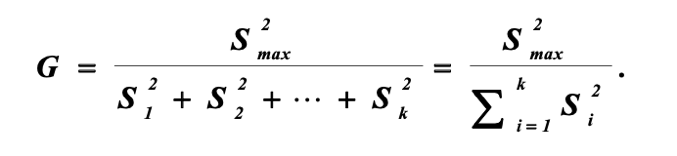
В случае, если эта величина меньше табличного значения критерия Кохрена с уровнем значимости α и числами степеней свободы n-1 и k, то у нас нет оснований отвергнуть гипотезу Н0:
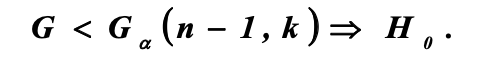
Пирсона:

7.Функциональные и стохастические связи:
Связи между технологическими параметрами условно можно разделить на функциональные и стохастические.
Функциональной называется такая связь между параметрами, которая может быть выражена в виде функциональной зависимости. Одним из примеров такой связи может служить закон Ома, связывающий силу тока, напряжение и электрическое сопротивление. Таким образом, функциональная связь преимущественно выражает зависимость между детерминированными, неслучайными величинами, однако она может также существовать и между величинами случайными, если значение одной случайной величины есть функция другой.
Стохастическая (или, что то же самое, – вероятностная) связь проявляется в том случае, когда какой-нибудь параметр (или параметры) влияет на случайную величину таким образом, что в результате этого влияния меняется закон распределения этой случайной величины. Типичным примером может служить связь между ростом и весом человека. Если мы выберем, например, множество людей с ростом 160 см, то их вес можно описать случайной величиной с определенными математическим ожиданием и дисперсией, а если взять множество людей с ростом 190 см, – то, очевидно, что случайная величина, описывающая их вес, будет иметь другое математическое ожидание и, может быть, другую дисперсию.
Регрессия:
Зависимость математического ожидания случайной величины от значения других (случайных или неслучайных) параметров называется регрессией или уравнением регрессии. Зависимая случайная величина называется откликом, а параметры, от которых отклик зависит — независимыми переменными или факторами. Обозначим отклик буквой y, а вектор факторов (т.к. факторов может быть много)

Структура данных для регрессивного анализа и его статистические предпосылки:
Структура экспериментальных данных для проведения регрессионного анализа выглядит следующим образом. Проведено N экспериментов при различных значениях вектора факторов x 1 , x 2 ,..., x N и измерено N со- ответствующих значений отклика y 1 , y 2 ,..., y N .
Общая постановка задачи регрессионного анализа:
Установление формы зависимости
Определение функции регрессии и установление влияния факторов на зависимую переменную
Оценка неизвестных значений переменной (экстраполяция и интерполяция)
Нормальные уравнения:
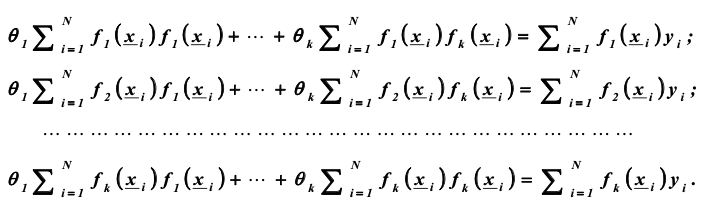
Система представляет собой систему из k линейных алгебраических уравнений с k неизвестными 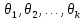
8.Линейный регрессионный анализ:
Линейным регрессионным анализом называется процедура нахождения оценок коэффициентов регрессии и статистического анализа результатов в случае, если математическая модель
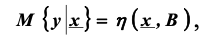
линейна по параметрам, т.е. имеет следующий вид:
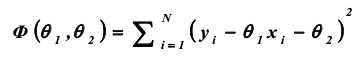
Общий вид нормальных уравнений:
Нахождение оценок коэффициентов уравнения регрессии:

9.Статистический анализ уравнения регрессии:
При нахождении и интерпретации регрессионных зависимостей каждый этап расчета должен сопровождаться статистическим анализом, необходимым как для проверки предпосылок регрессионного анализа, так и для получения содержательных выводов по его результатам. Рассмотрим основные этапы этого анализа.
Проверка предпосылок регрессионного анализа:
Для нахождения оценок необходимо также, чтобы выполнялись следующие условия, которые называются предпосылками регрессионного анализа:
1) отклики y 1 , y 2 ,..., y N представляют собой независимые, нормально распределенные случайные величины;
2) дисперсии всех значений откликов равны, т.е. проверена статистическая гипотеза о равенстве этих дисперсий;
3) независимые переменные (факторы) x x1 , x2 ,… , xq T измеряются с ошибкой, пренебрежимо малой по сравнению с ошибкой откликов, что позволяет считать их неслучайными величинами.
Адекватность модели:
Адекватность модели – это соответствие модели и эксперимента.
Дисперсия предсказания:
Статистка дисперсии предсказания выглядит таким образом,
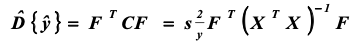
Доверительный эллипсоид оценок коэффициентов уравнения регрессии:
Доверительные интервалы одномерных случайных величин – это такие интервалы, которые содержат внутри себя истинное значение оцениваемого параметра с заданной вероятностью. С геометрической точки зрения они представляют собой отрезок прямой. Многомерным обобщением доверительного интервала является доверительная область. По определению доверительной называется такая область k-мерного пространства, которая с заданной вероятностью содержит в себе истинное значение оцениваемого k-мерного вектора. Применительно к вектору оценок коэффициентов уравнения регрессии доверительная область – это такая часть k-мерного пространства коэффициентов регрессии, которая с заданной вероятностью содержит в себе вектор истинных значений этих коэффициентов.
 |
|
|
 Скачать 0.9 Mb.
Скачать 0.9 Mb.
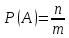
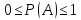
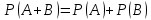
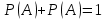
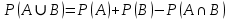
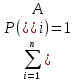

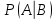 и
и 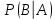 – условные вероятности
– условные вероятности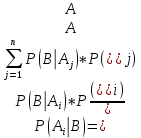
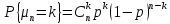 ,
,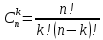 – биноминальный коэффициент или, что то же самое, число сочетаний из n по k.
– биноминальный коэффициент или, что то же самое, число сочетаний из n по k. 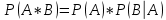
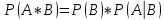
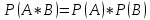
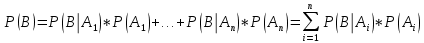
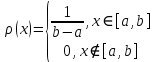
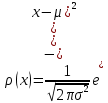
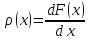
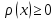 , что с учетом формулы выше следует из того, что функция распределения – неубывающая.
, что с учетом формулы выше следует из того, что функция распределения – неубывающая. 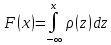
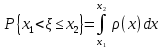 .
.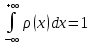
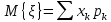
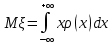
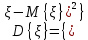
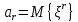
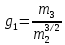
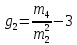

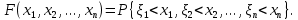
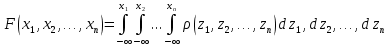
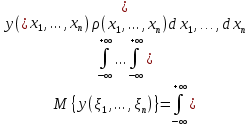
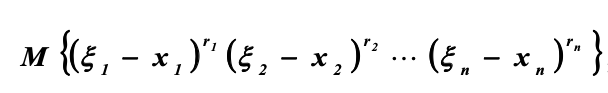
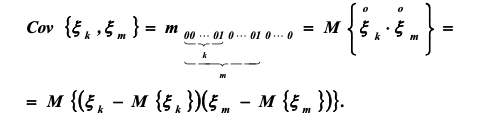
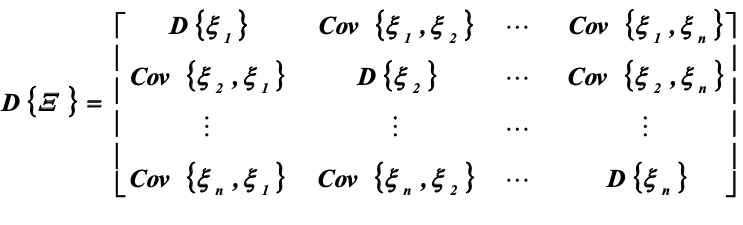
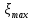 и наименьшее
и наименьшее 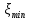 значения. Интервал [
значения. Интервал [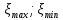 ] разбивается на k интервалов. Затем проводится подсчет количества попаданий ri случайных величин из выборки в каждый i интервал.
] разбивается на k интервалов. Затем проводится подсчет количества попаданий ri случайных величин из выборки в каждый i интервал. 
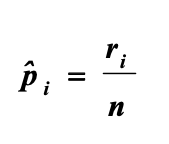
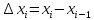 , а вторая (высота).
, а вторая (высота).